Бесплатный фрагмент - Gold Trader

Четные степени Интеграла Гаусса связь с гамма-функцией

Связь чётных степеней интеграла Гаусса с гамма-функцией выражается следующим образом:

Рассмотрим интеграл вида

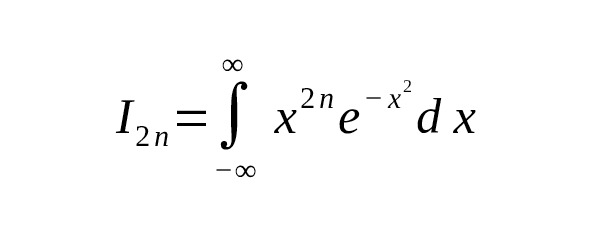
где — чётная степень.

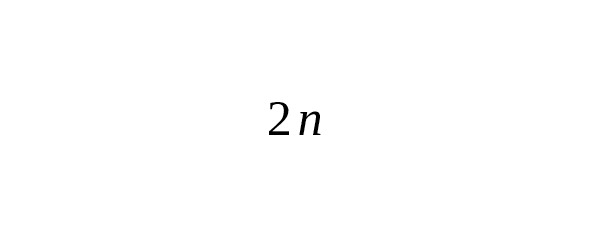
Этот интеграл выражается через гамма-функцию так:

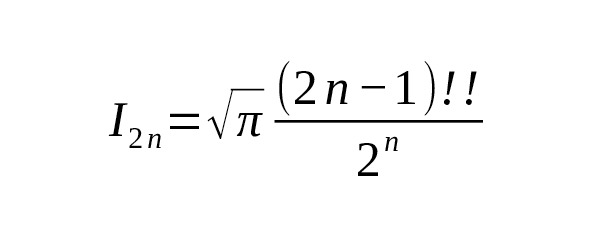
или, используя свойства гамма-функции:

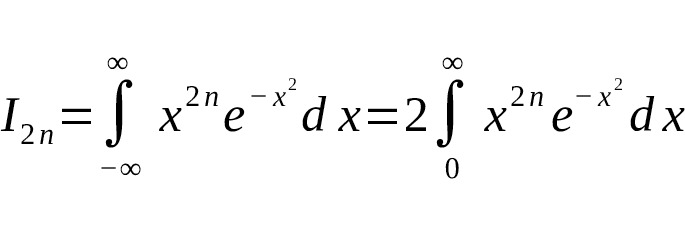
Замена переменной $ t = x^2 $ приводит к гамма-функции:

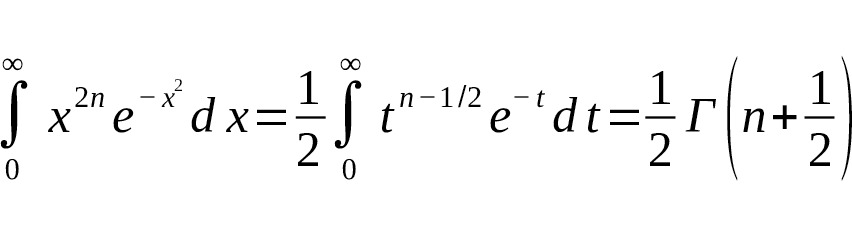
Таким образом,

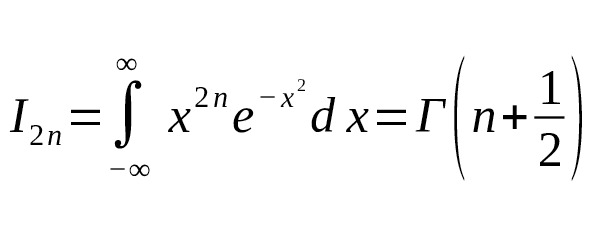
— Чётные моменты гауссового интеграла выражаются через гамма-функцию от полуцелого аргумента.

— Для общего случая: где для стандартного Гаусса $ m=2n,,a=1,,b=2 $ [1] [2].

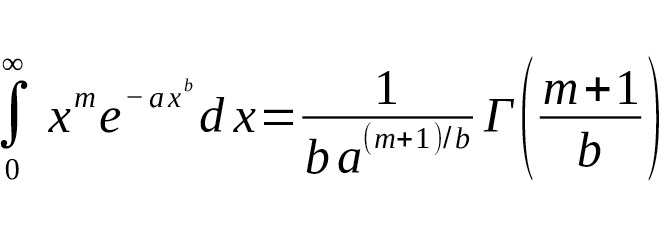
Это показывает прямую связь между чётными степенями интеграла Гаусса и значениями гамма-функции, и объясняет, почему значения при полуцелых аргументах выражаются через $ \sqrt {\pi} $ [1] [2].

— Например, для $ n=0 $ (то есть стандартный интеграл Гаусса):

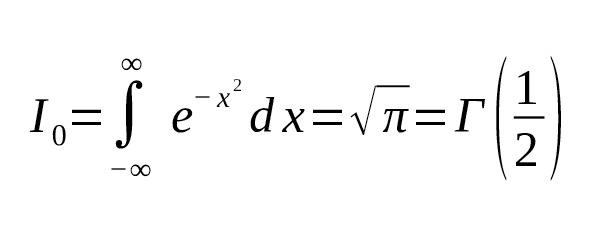
— Для $ n=1 $:

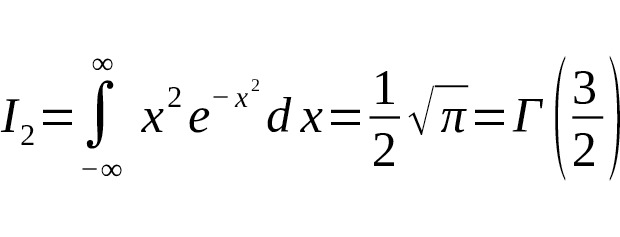
То есть значения чётных моментных интегралов Гаусса прямо выражаются через гамма-функцию для полуцелых аргументов [1] [2].

Примеры использования:

⁂

Перечисли литературу на данную тему

Основные источники по теме интегралов Гаусса с четными степенями и связанных с этим тем квадартур, вычисления и применения:

— Фихтенгольц Г. М. «Курс дифференциального и интегрального исчисления», т.2. Классический учебник, подробно рассматривает гауссовы интегралы, их свойства и вычисления [3].

— Крайнов В. А. «Численные методы вычисления определенного интеграла». В пособии разбираются методы точного и приближенного вычисления интегралов, в том числе гауссовых, обсуждается точность для многочленов четной степени и приводятся формулы [4].

— Fedotov A.A. «Численные методы интегрирования». Современное пособие с практическими примерами численного вычисления гауссовых интегралов и их приложениями [5].

— Пастухов Д. Ф. «Квадратуры Гаусса. Интегральные уравнения». Методические указания по построению и применению квадратурных формул Гаусса для вычисления интегралов от многочленов даже высокой степени [6].

— Добрынина С. В. «Квадратурные и кубатурные формулы». Пособие содержит практические задания и разбор правил приближенного интегрирования, в том числе формулы Гаусса для интегралов с весами и многочленами [7].

— Арушанян И. О. «Алгоритмы приближенного вычисления интегралов». Обсуждаются методы вычисления интегралов с различными степенями точности, включая использование четных степеней в гауссовых интегралах [8].

Эти книги и пособия подходят для углубленного изучения вычисления и теории гауссовых интегралов, их свойств и приложений.

⁂
Теоретические основы квадратурных формул

Квадратурные формулы — это классический математический инструмент для приближённого вычисления определённых интегралов по значениям функции в конечном числе точек. Их основная задача — заменить вычисление интеграла суммой, где коэффициенты и точки выбора (узлы) подбираются для достижения максимальной точности на определённом классе функций [9] [10] [11].

Общий вид квадратурной формулы

Любая квадратурная формула обычно имеет следующий вид:

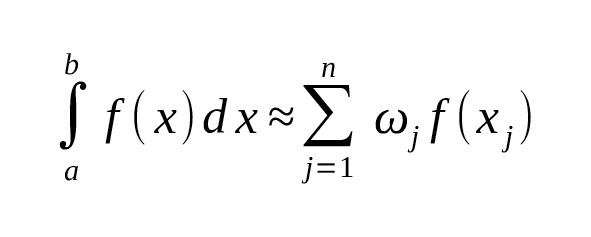
где:

— — узлы формулы (точки, в которых вычисляется функция),

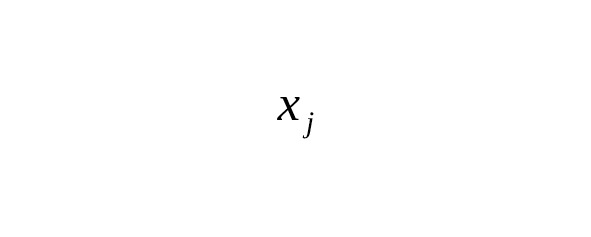
— — веса (коэффициенты, с которыми берется значение функции в узлах).

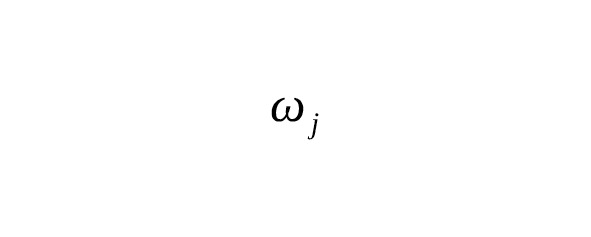
Теоретические положения

— Точность квадратурной формулы определяется тем, для какого класса функций формула дает точное значение интеграла. Обычно это многочлены степени не выше некоторого значения.

— Погрешность (остаточный член) квадратурной формулы показывает, насколько точно аппроксимируется интеграл [10] [12].

— Выбор узлов и весов: Например, в формулах Ньютона–Котеса узлы равноотстоящие, а в формулах Гаусса — это корни ортогональных многочленов (например, многочленов Лежандра для классического интеграла на отрезке), что позволяет добиться наивысшей алгебраической степени точности — для узлов [11].

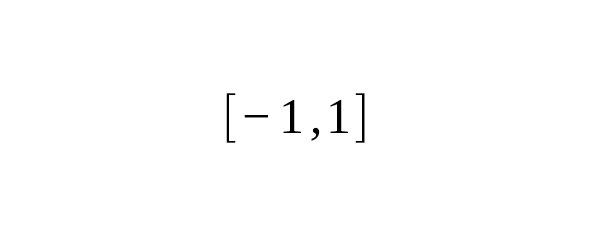
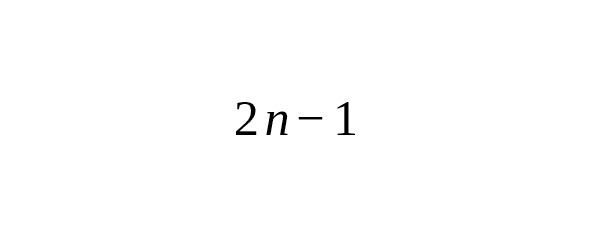
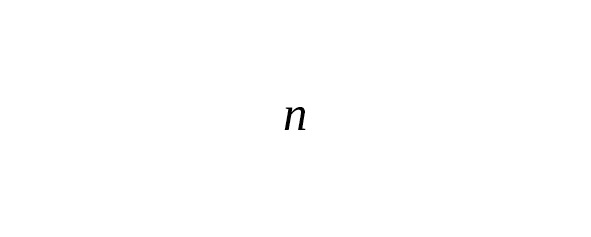
— Историческая основа: методы приближенного интегрирования возникли еще во времена Ньютона и Лейбница. Построение классических формул (прямоугольников, трапеций, Симпсона) базируется на замене функции внутри отрезка некоторым простым приближением (полиномом) и интегрировании этого приближения [10].

Виды квадратурных формул

— Интерполяционные квадратурные формулы: базируются на интерполяции функции (чаще всего полиномиальной) [11].

— Составные (разбиение интервала): длинный интервал делится на части, и на каждом применяется простая формула (например, составная формула трапеций или Симпсона) [12] [11].

— Взвешенные квадратурные формулы используются, когда подынтегральная функция содержит особенности (например, сингулярности или быстрый рост) [10] [13].

Погрешность и степень точности

— Степень точности — это наибольшая степень многочлена, для которого формула даёт точный интеграл.

— Погрешность оценивается через верхнюю границу производных высокого порядка подынтегральной функции (обычно формула тейлоровского остатка) [11] [10] [9].

Примеры

— Прямоугольников:

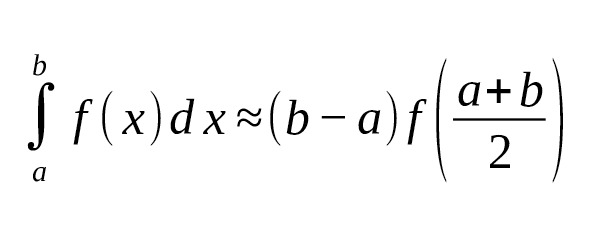
— Трапеций:

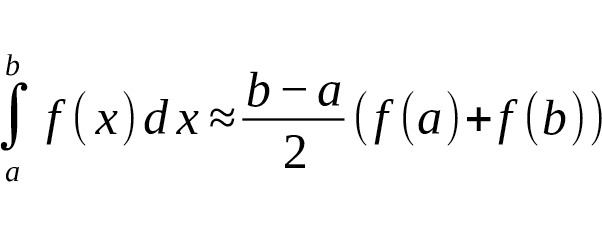
— Симпсона: точна для многочленов до степени [9] [12]

Итог

Квадратурная формула — результат строго математического построения, в котором выбор узлов и весов приводит к компромиссу между точностью и вычислительной простотой. Вся теория квадратурных формул сводится к задаче оптимального приближения интеграла функцией суммирования с максимально возможной точностью при минимальных вычислительных затратах [11] [10] [9].

⁂

Интеграл Гаусса равный Гамма функции

Связь между интегралом Гаусса и гамма-функцией выражается через интегралы от степеней $ x $ с показательной функцией и замены переменных. Классический интеграл Гаусса выглядит так:

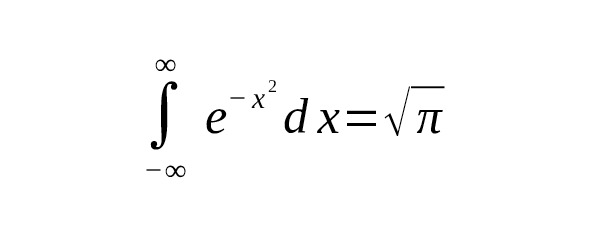
Гамма-функция по определению:

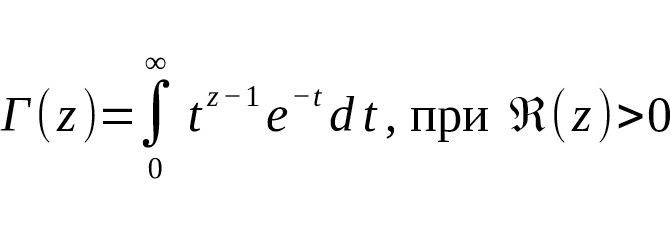
[14] [15] [16]

При определённых значениях аргумента эта функция вычисляет интегралы, очень близкие по форме к гауссовым. Например, для интегралов вида:

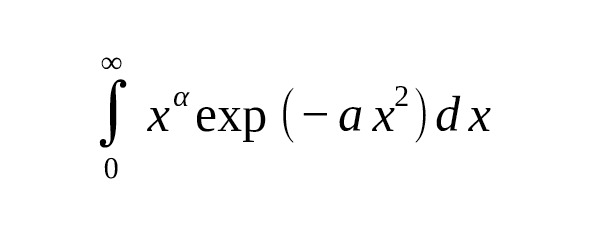
выражение можно записать через гамма-функцию:

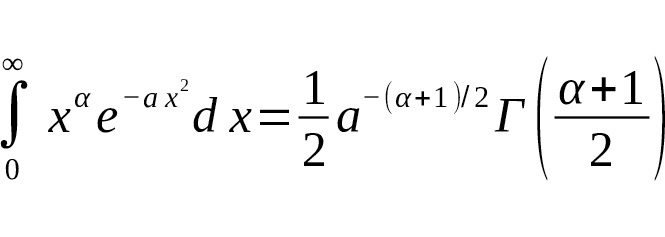
Это означает, что интегралы «гауссового» типа с четными и нечетными степенями $ x $ напрямую связаны с гамма-функцией от полуцелого (дробного) аргумента [14] [17].

Гауссов интеграл — частный случай этого выражения при и. Тогда

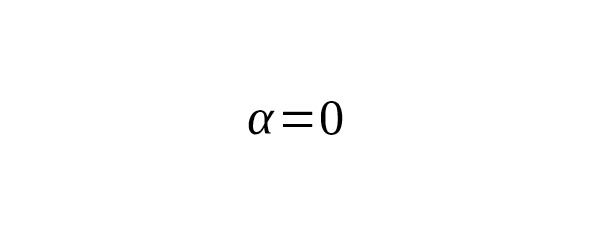
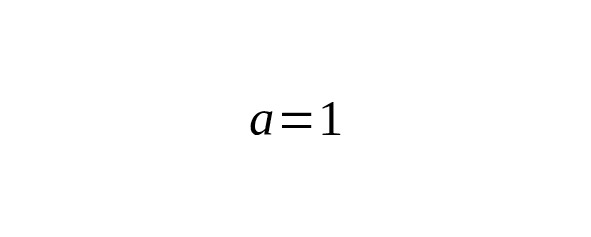
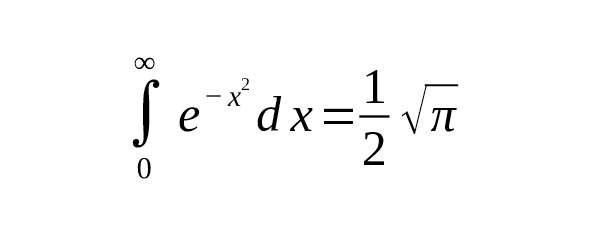
или, что то же самое:

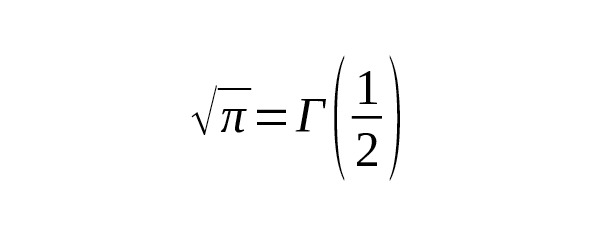
То есть, [14] [17].

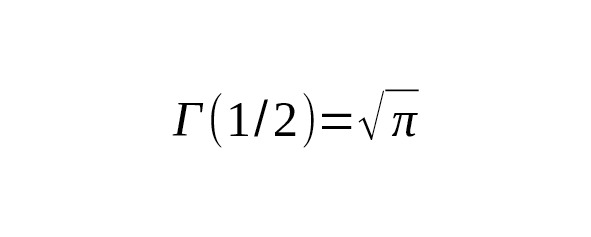
Итак:

— Интеграл Гаусса выражается через значения гамма-функции, особенно в случае нецелых (чаще полуцелых) аргументов.

— Более общая формула связывает интегралы вида с и параметром [14] [17].

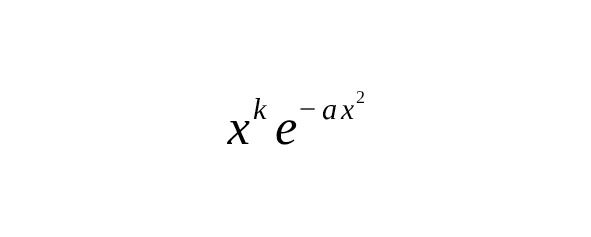
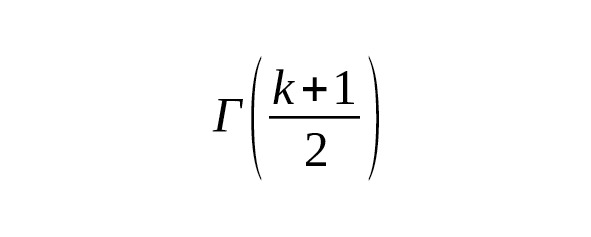
Эти связи активно используются для вычислений в теории вероятностей, физике и математике.

⁂

Связь интеграла Гаусса и гамма-функции

Связь между интегралом Гаусса и гамма-функцией проявляется в вычислении интегралов вида $ \int_0^ {\infty} x^ {\alpha} e^ {-a x^2} dx $, которые можно выразить непосредственно через гамма-функцию с полуцелым аргументом:

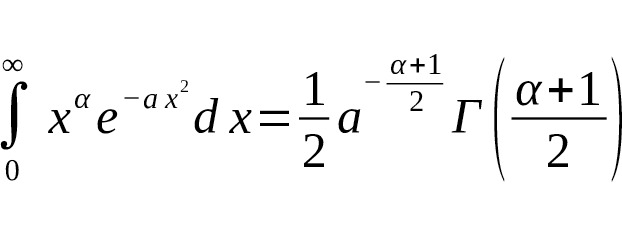
Здесь $ a> 0 $, $ \alpha> -1 $, а $ \Gamma (z) $ — гамма-функция.

Классический интеграл Гаусса:

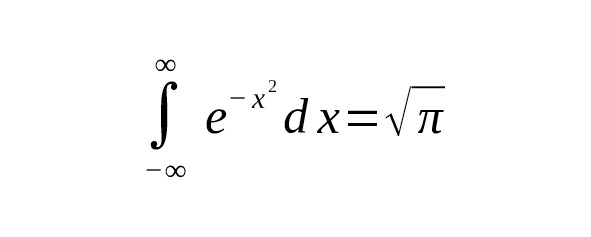
является частным случаем, когда и, но взятым по всей оси. Для полуинтервала:

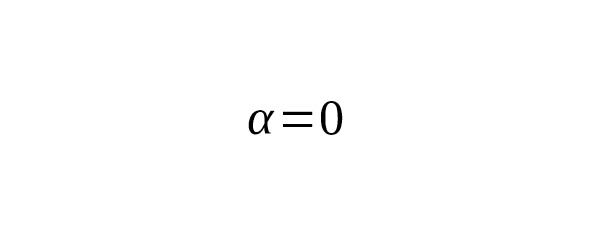
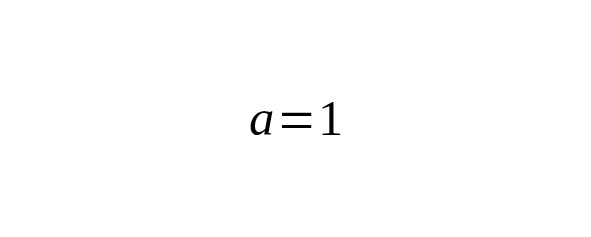
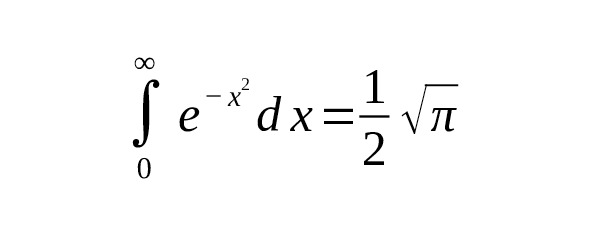
что согласуется с тем, что.

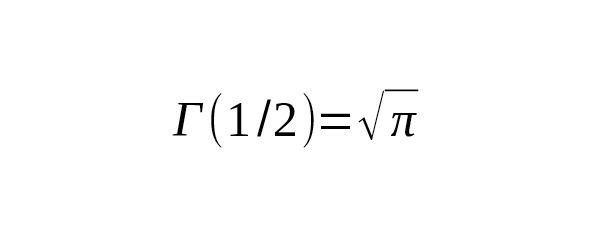
Таким образом:

— Все интегралы вида выражаются через -функцию с аргументом.

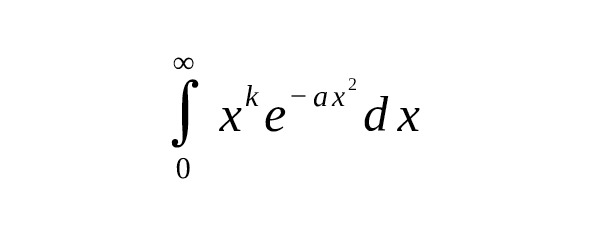
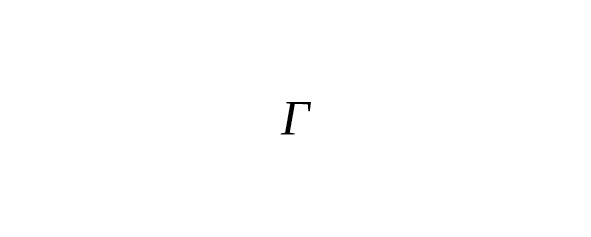
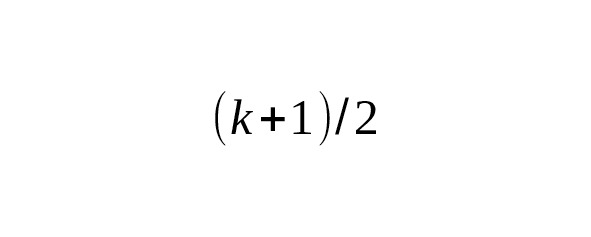
— Значение гауссова интеграла — это не что иное, как по определению гамма-функции.

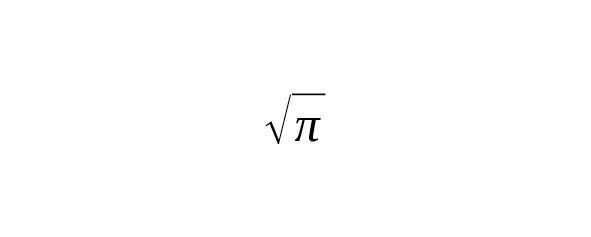
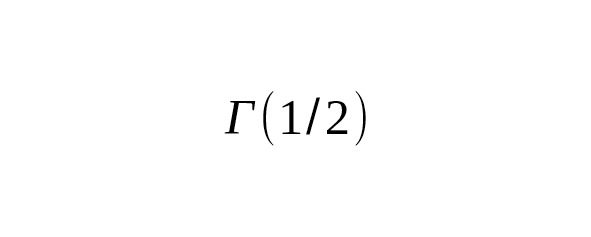
Эта связь позволяет вычислять так называемые моменты нормального распределения и использовать результаты для аналитических и численных задач в математике, статистике и физике.

Проанализируй данные равенства

На изображении представлены важные интегралы, связанные с гауссовой функцией $ e {-x2} $ и её степенями, а также их аналитические выражения.

Анализ равенств

— Вид интегралов

Большинство интегралов имеют следующий вид (на всю ось или полуось):

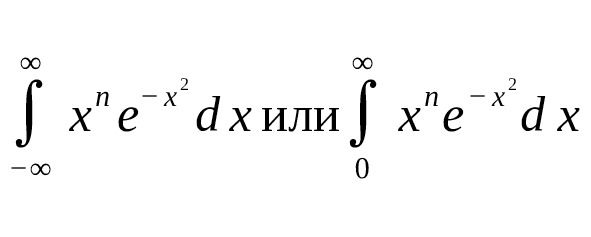
где $ n $ — целое неотрицательное число.

— Нечётные степени

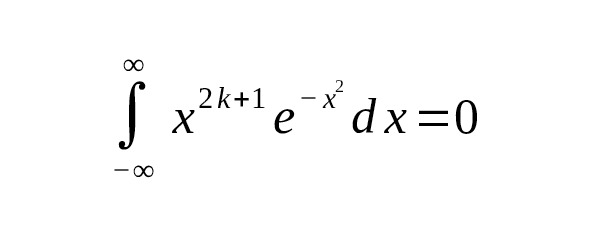
Это справедливо из-за нечетности функции: четные степени чётны, нечётные — нечетны, а $ e {-x2} $ чётная. Интеграл от нечётной функции на симметричном интервале даёт ноль.

— Чётные степени

Интегралы от чётных степеней образуют непустую последовательность:

— Для $ n=0 $:

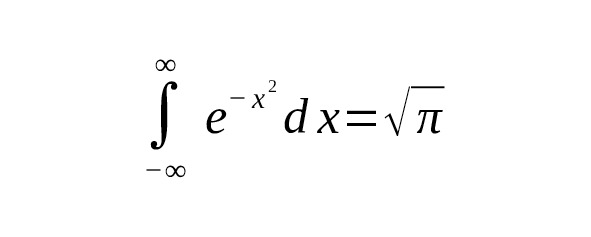
— Для $ n=2 $: