
Бесплатный фрагмент - Занимательная комбинаторика
Предисловие
В повседневной жизни мы часто сталкиваемся с ситуациями, когда нам необходимо рассадить гостей за столом, составить букеты из имеющихся цветов, подсчитать количество выигрышных билетов в лотерее и т. д. Но задумывались ли вы, сколькими вариантами мы можем это сделать? На этот вопрос помогает ответить комбинаторика — раздел математики, изучающий задачи выбора и расположения элементов из некоторого множества в соответствии с заданными правилами.
Формулы и методы комбинаторики широко используются в теории вероятностей для подсчета вероятности случайных событий.
Комбинаторика как самостоятельная наука появилась в XVIII веке. Рождение комбинаторики связано с трудами Блеза Паскаля и Пьера Ферма по теории азартных игр. Большой вклад в развитие комбинаторики методов внесли Готфрид Вильгельм Лейбниц, Яков Бернулли, Леонард Эйлер и другие выдающиеся ученые.
Перестановки
Однажды в выходной день Маша решила навести порядок в своих игрушках и рассадить в ряд медвежонка, куклу и львёнка.
Вначале она рассадила их так:

Но ей не понравилось, что медвежонок сидит рядом со львёнком. Тогда Маша пересадила игрушки следующим образом:

Но и тут Маша не смогла определиться, кто должен сидеть справа от куклы — львёнок или медвежонок?
Так бы Маша и продолжала бы переставлять игрушки с места на место, если бы в комнату не вошел Машин папа.
— Ты чем это занимаешься? — поинтересовался он у Маши.
— Да вот, — грустно вздохнула Маша, — пытаюсь расставить игрушки, но у меня что-то не получается. Столько много разных вариантов, а мне ни один не нравится.
— Допустим, — не согласился папа, — что вариантов не так уж и много. У тебя три игрушки, значит, вариантов всего шесть.
— Как ты так быстро посчитал? — удивилась Маша.
— Есть такая наука, — пояснил папа, — комбинаторика. Она и занимается подсчетом различных вариантов перестановок. Допустим у тебя всего две игрушки — медвежонок и кукла. Их можно переставить только двумя способами:


Если у тебя три игрушки, то это можно сделать уже шестью способами:

— А если у меня четыре игрушки? — спросила Маша.
— Тогда существует 24 варианта различных способов их перестановки. В комбинаторике такие упорядочения множества, состоящего из определенного количества элементов, так и называют — перестановками. Особенностью перестановок является то, что в них должны участвовать все элементы данного множества.
Количество всех возможных перестановок можно найти по формуле, где n — количество элементов данного множества.
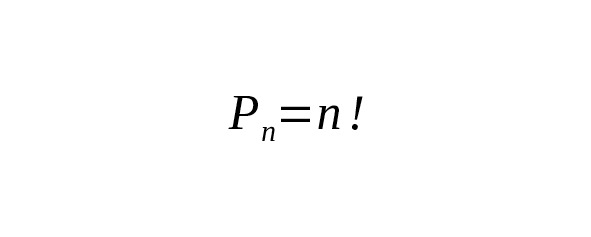
Символ n! называется факториалом и обозначает произведение всех целых чисел от 1 до n.
.
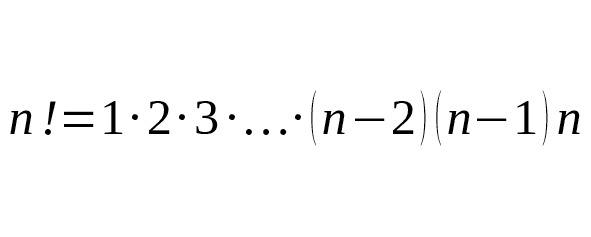
Например, 3!=1∙2∙3=6. 4!=1∙2∙3∙4=24.
При вычислении факториала принято считать, что 0!=1, 1!=1.
— А если у меня пять игрушек? — не унималась Маша.
— В таком случае у тебя 1∙2∙3∙4∙5=120 вариантов перестановок.
— Так много? — удивилась Маша.
— А если множество состоит из 6 элементов, — продолжал папа, — то число перестановок будет равняться 720. Для 7 элементов число перестановок будет равно 5040, для 8 — 40320 и так далее. Чем больше число элементов, тем больше число перестановок.
— А если вместо пяти игрушек взять пять конфет? — спросила Маша. — Число перестановок изменится?
— Если конфеты все различные, то, как и в случае с игрушками число перестановок все равно будет 120.
— То есть, — заключила Маша, — число перестановок не зависит от того, что я переставляю — игрушки, конфеты или еще что-нибудь?
— Совершенно верно! — подтвердил папа. — Главное, чтобы в перестановках участвовали все элементы множества, и элементы должны быть различными.
— Посчитать число перестановок несложно, — согласилась Маша, — а вот переставить игрушки и не запутаться при этом гораздо сложнее.
— Для того чтобы не запутаться, — успокоил Машу папа, — можно использовать дерево возможных вариантов. Одолжим на время у мамы пуговицы.
В первый ряд положим 3 пуговицы разного цвета. Мы уже считали, что возможных перестановок для трех элементов равно шести.

Второй ряд, он будет у нас вспомогательным, мы составим следующим образом:

— То есть мы добавили пуговицы других цветов? — предположила Маша.
— Совершенно верно. В третьем ряду мы просто поменяем пуговицы местами. Вот так:

— А что мы будем делать с четвёртым рядом? — поинтересовалась Маша.
— А четвертого ряда не будет, — ответил папа. У нас три пуговицы, то есть три элемента множества, значит и рядов будет три. Осталось только, следуя сверху вниз, перечислить все варианты перестановок:
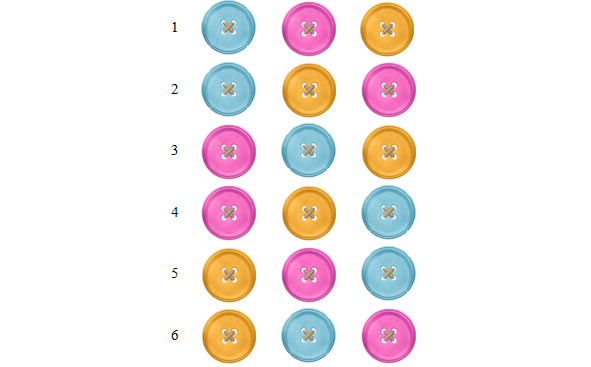
И совсем несложно. Главное быть внимательным.
— Как интересно! — воскликнула Маша. — А если у меня все-таки есть одинаковые игрушки, то количество перестановок считается точно также?
— Не совсем, — пояснил папа. — Если некоторые элементы множества повторяются, то такие перестановки называются перестановками с повторением.
Перестановки с повторением
— Пусть у тебя есть два одинаковых медвежонка.
— Но у меня нет двух одинаковых медвежонка, — возразила Маша.
— Хорошо, — согласился папа. — Тогда возьмем два зеленых карандаша и один красный.

Карандашей всего 3, значит, число перестановок равно 6. Но нет разницы, если поменять зеленые карандаши местами. Мы получим тот же самый вариант. Поэтому число перестановок с повторением будет всего 3:
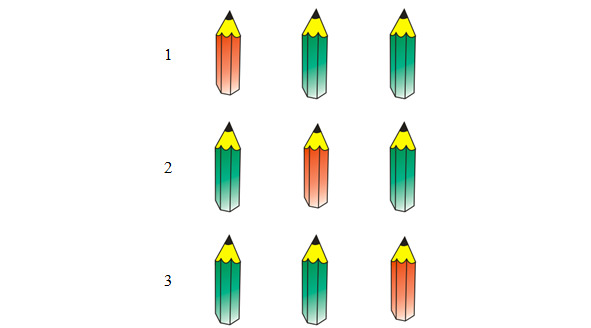
— То есть, — предположила Маша, — если есть одинаковые элементы, то перестановок будет меньше.
— Да. Пусть множество состоит из n1 элементов одного вида, n2 элементов другого вида и т. д. Всего элементов n1+n2+…+nk=n. Тогда число перестановок с повторением равно.
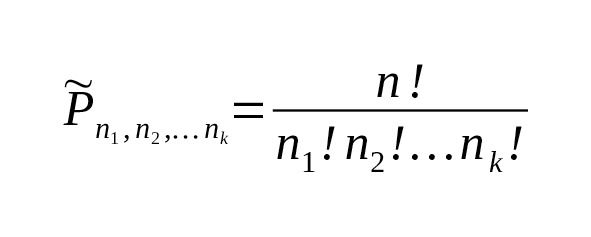
— Какая сложная формула! — воскликнула Маша.
— Нисколько, — возразил папа. — И ты сама сейчас в этом убедишься. Пусть у нас есть карандаши. Два красных, один зеленый и один синий. То есть n1=2, n2=1, n3=1. Всего карандашей n1+n2+n3=2+1+1=4. Следовательно, число перестановок с повторением равно.
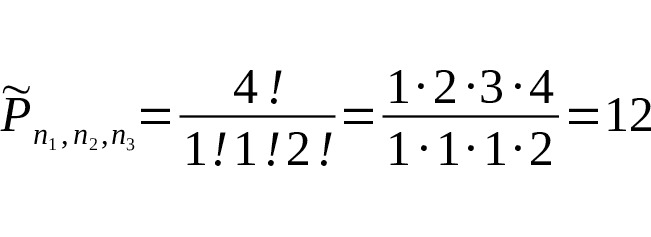
— Хорошо, — согласилась Маша. — А если у меня есть карточки с буквами из которых составляют слова? Буквы же в словах могут повторяться.
— И сколько ты хочешь взять карточек?
— Сейчас, — Маша открыла ящик стола и вытащила наружу карточки с буками. — Вот. Это у меня ещё с первого класса осталось.
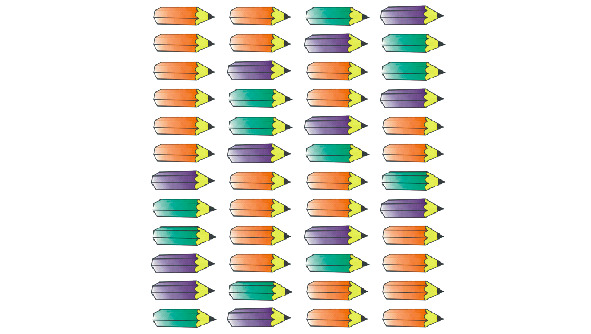
— Давай посмотрим, — папа разложил на столе карточки. — У нас есть три буквы А, две буквы У и две буквы М.

— Всего семь, — подсказала Маша.
— Воспользуемся формулой для перестановок с повторением.. Значит, существует 210 вариантов перестановок.
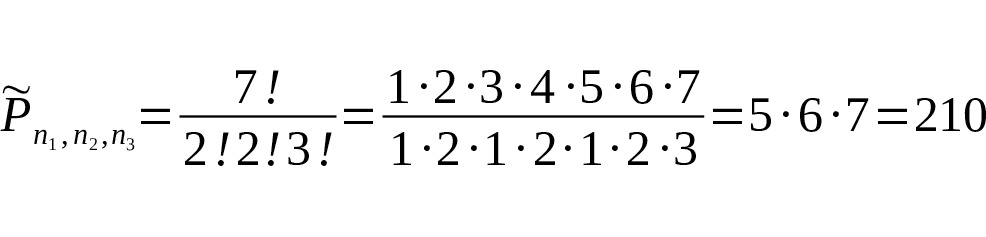
— Так много? — удивилась Маша.
— Так много, — подтвердил папа. — А если у нас есть имеются другие наборы элементов, то и число перестановок будет другим.
— А можно я теперь попробую сама?
— Конечно. А что мы будем считать?
— У меня есть цветные скрепки.

Три зеленых, три синих, три желтых и две красных. Всего 11 скрепок. Значит, число перестановок будет равно.
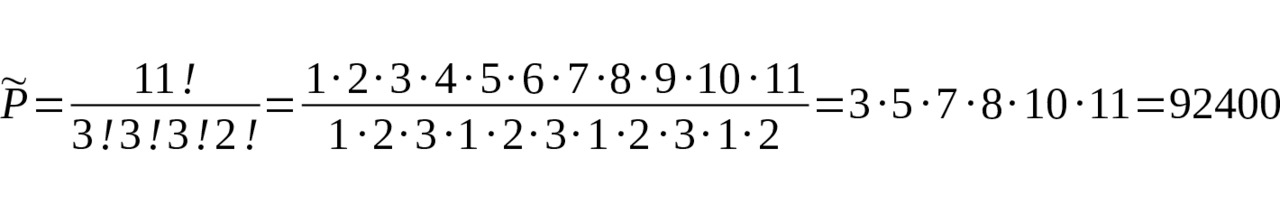
Вот так число! Это сколько же времени уйдет на то, чтобы переложить все скрепки?
— Перекладывать скрепки мы не будем, — возразил папа. — А ты мы на это дело потратим все выходные. А тебе еще уроки учить нужно. Да и у меня есть дела.
— Ну, папа! — заныла Маша. — Давай еще что-нибудь посчитаем!
— В другой раз, — ответил папа. — Тем более что в комбинаторике изучаются не только перестановки. А это тебе задачки для самостоятельного решения:
1. В купе поезда едут папа, мама, сын и дочь. Сколько есть вариантов размещения семьи в купе?
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
