
Предисловие
Это пособие мало похоже на учебник. Скорее, его можно назвать рабочей тетрадью, которая переводит «математический язык на русский». Работая по тетради, вы не найдете определений, в которых нужно долго разбираться, не обнаружите формул, которые придется нудно зубрить. Да, да, формулы учить не придется! Удивлены?
Вероятно, само слово «тригонометрия» до сих пор ввергает вас в ужас и уныние. И неудивительно, ведь формулы — это первое, что приходит в голову. Уже видели такую картинку?

«Это выучить невозможно!» — думаете вы. Я тоже когда-то так думала. Однако решающий момент — точка невозврата — наступил: мне предстояло объяснить эту тему 10-классникам. На глаза попалось пособие 1983 года выпуска «Тригонометрические функции» В. С. Крамора и П. А. Михайлова. Я его тщательно изучила. Стало понятно, откуда взялась каждая формула, и теперь я могла объяснить основы даже третьекласснику.
За годы работы у меня сложилась авторская методика обучения. Все мои ученики умеют решать задания по тригонометрии из ЕГЭ. А теперь и вы — мой ученик, а значит, и у вас получится. Для этого изучайте последовательно (важно!) ВСЕ уроки, выполняйте ВСЕ задания для отработки навыков, и уже очень скоро слово «тригонометрия» будет вызывать у вас улыбку, а ваши успехи удивят одноклассников и учителей! Дерзайте! Позвольте себе оценить красоту еще одного важнейшего раздела математики!
Раздел I
Урок 1. Числа на координатных осях

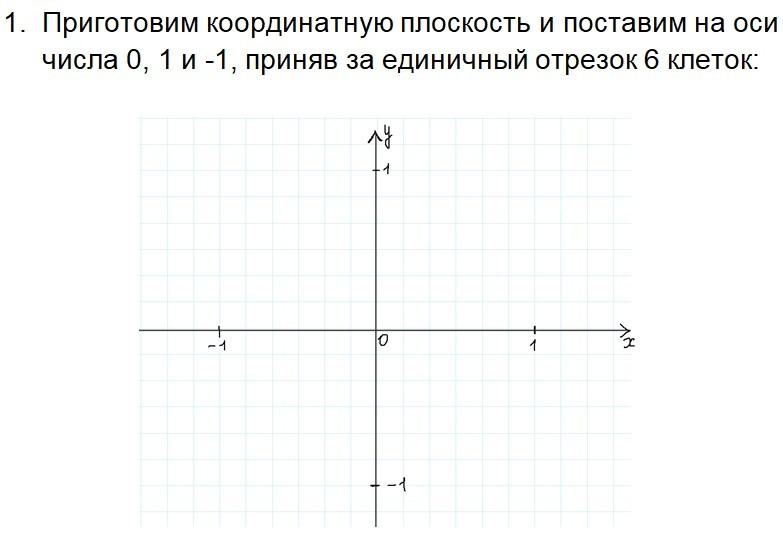
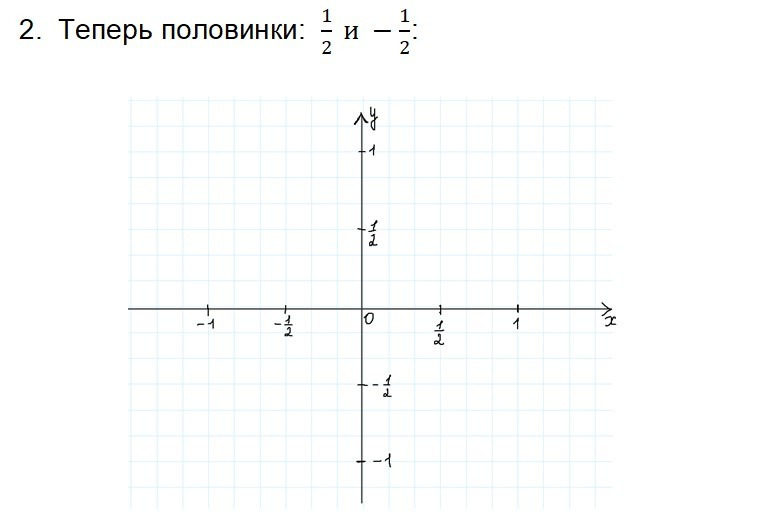
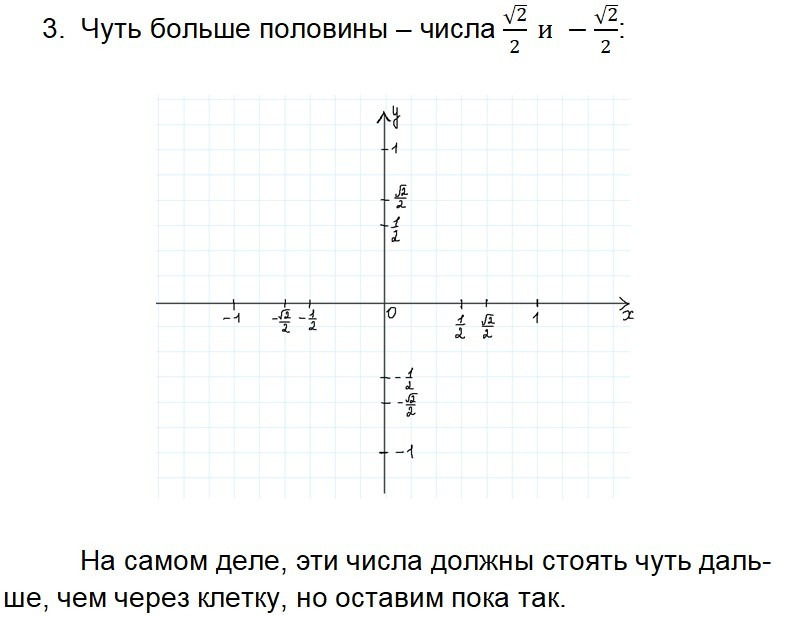
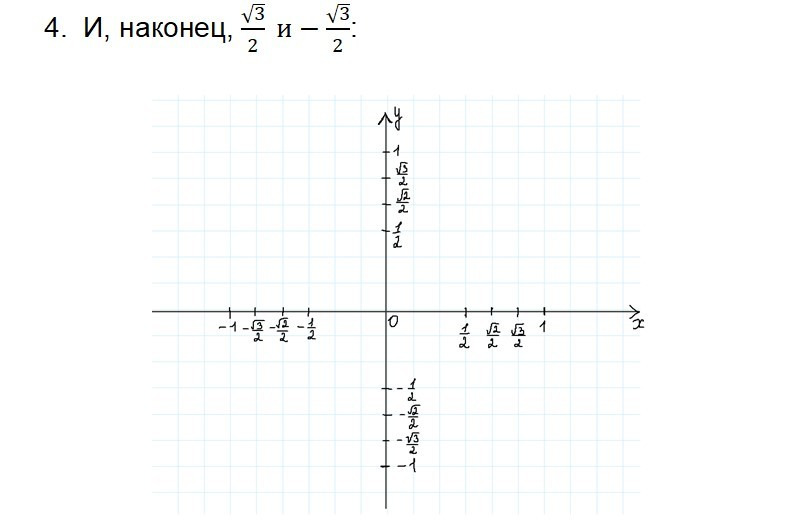
Урок 2. Числа на окружности

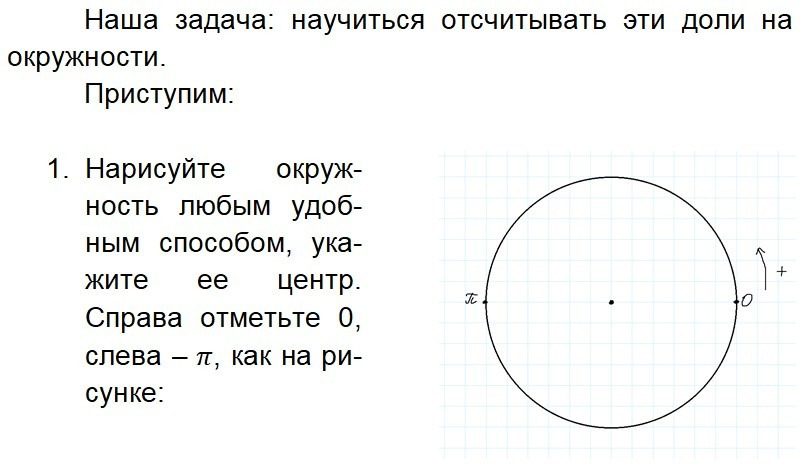
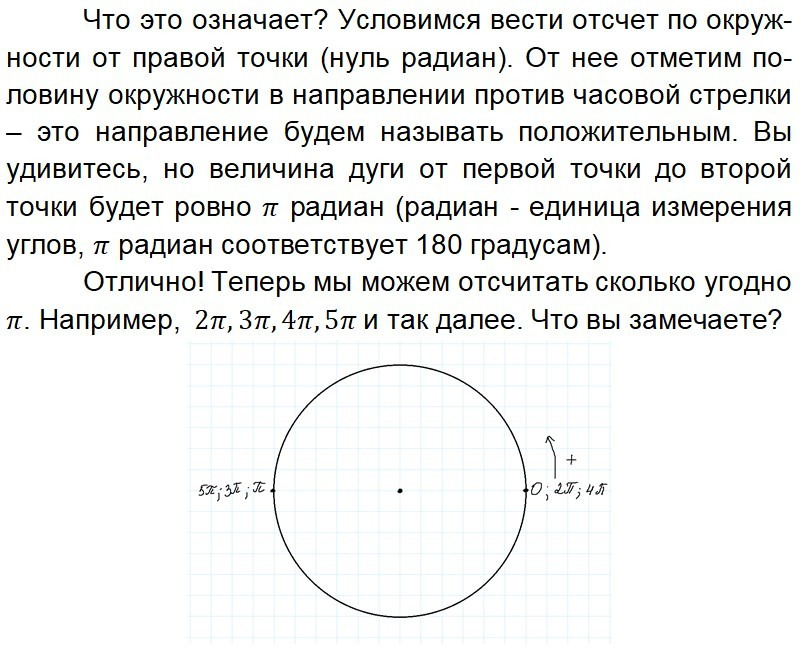

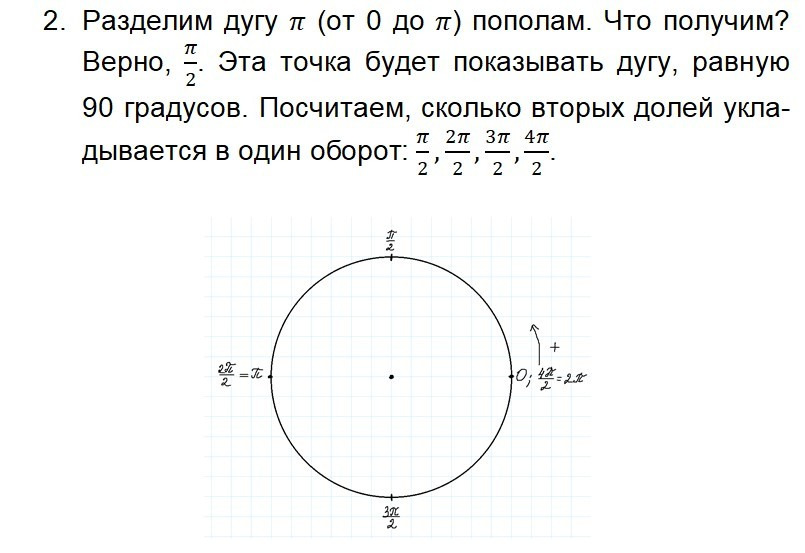

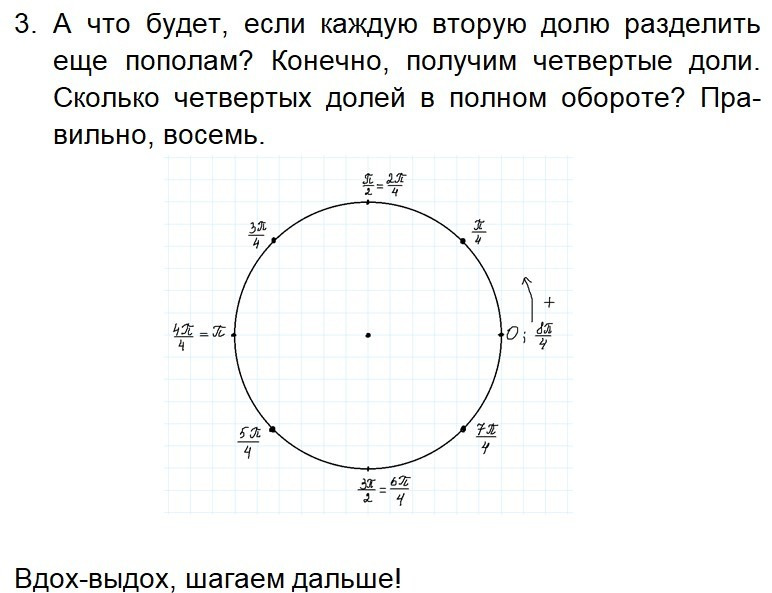
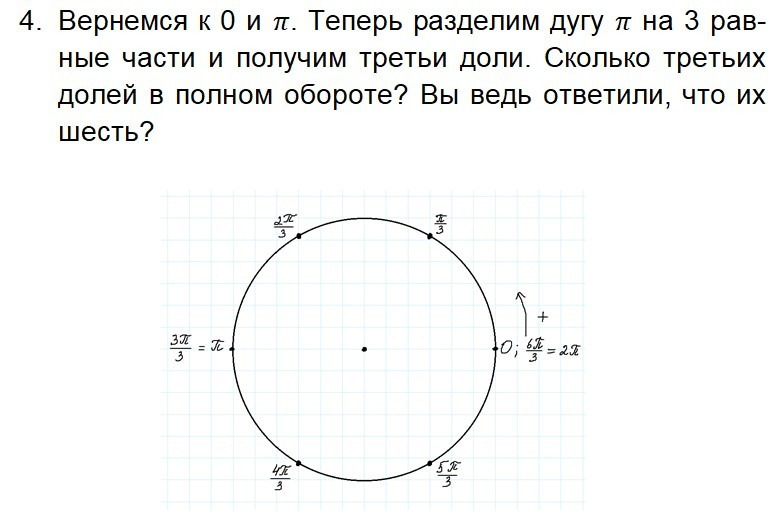
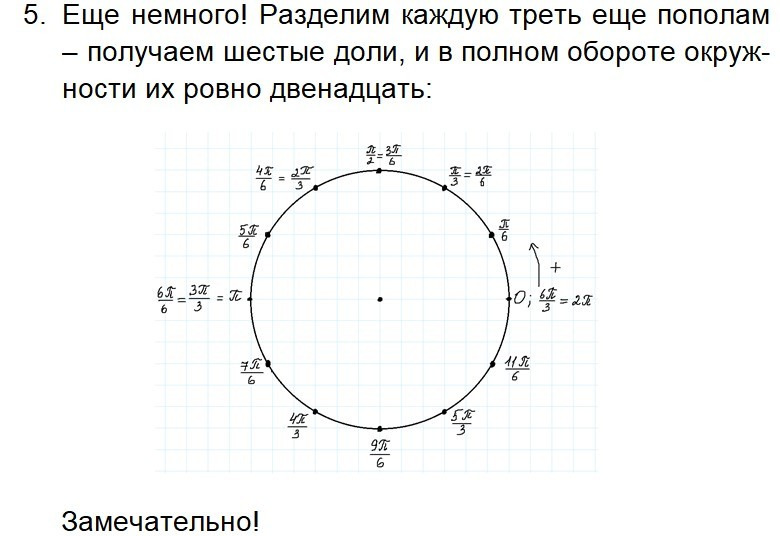
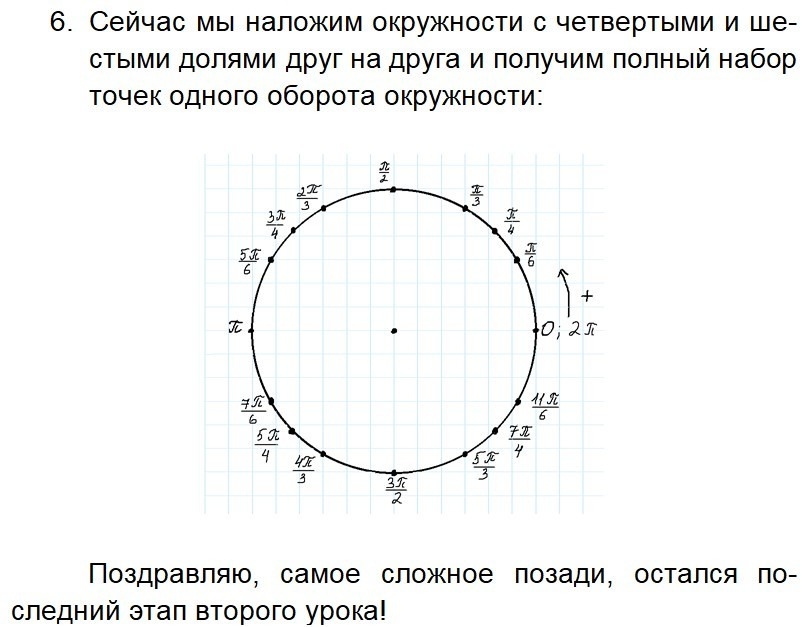
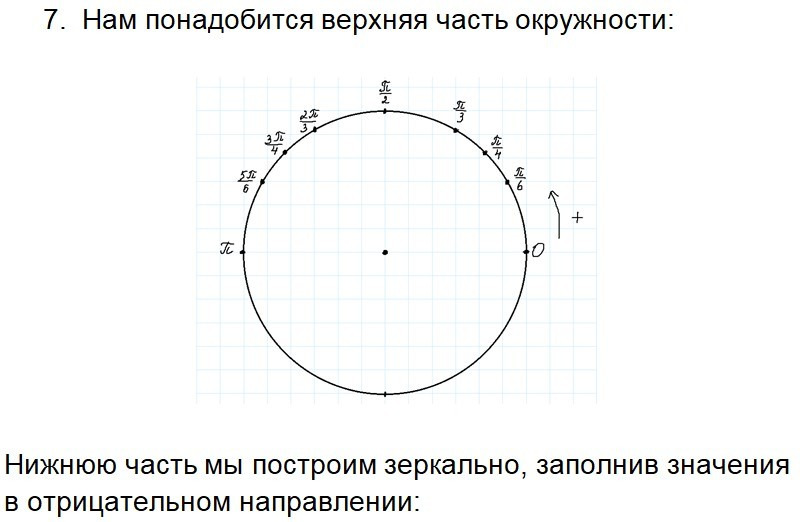
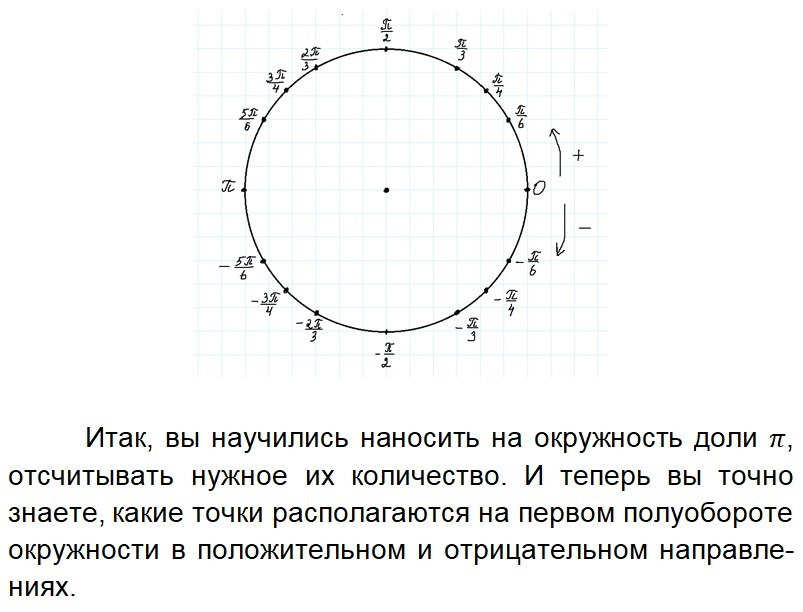

Урок 3. Координаты точек. Построение тригонометрического круга
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
