Бесплатный фрагмент - Тригонометрия: эти синусы, косинусы…

Предисловие

Тригонометрия… Уже наслышаны об ужасах этого раздела математики и переживаете, что ничего не поймете, а на экзамене не сможете решить задания с синусами/косинусами? Или уже изучили и ничего не поняли, а экзамен маячит впереди и ехидно машет ручкой (гелевой, черной)? Ох, как я вас понимаю! И сейчас же хочу развеять весь этот ужас, потому что смогу показать, что изучать тригонометрию легко и увлекательно!

Написав книгу «Тригонометрия — это просто!» для учащихся 10—11 классов, обнаружила, что непонимание, а значит, и непринятие закладывается гораздо раньше, при изучении геометрии в 8 классе, при первом знакомстве. И здесь выражаю благодарность Любови Григорьевне Татариновой, учителю физики с многолетним стажем. Именно она посоветовала мне написать книгу и для ребят 8—9 классов:

И вот, книга готова! С удовольствием представляю ее вашему вниманию!

Раздел I

Введение

Давайте разберемся, а что такое вообще тригонометрия? Посмотрим вашему страху прямо в глаза! Готовы?

Слово «тригонометрия» (страшно?) переводится как… «измерение треугольников». Да, да, и всего лишь! Треугольников вы не боитесь, верно? Вот и славно. Так что будем измерять треугольники. А поэтому изучение тригонометрии мы начнем именно с треугольника. Прямоугольного.

Урок 1. Прямоугольный треугольник

Тут все просто: если один из углов треугольника прямой, то треугольник называется прямоугольным.

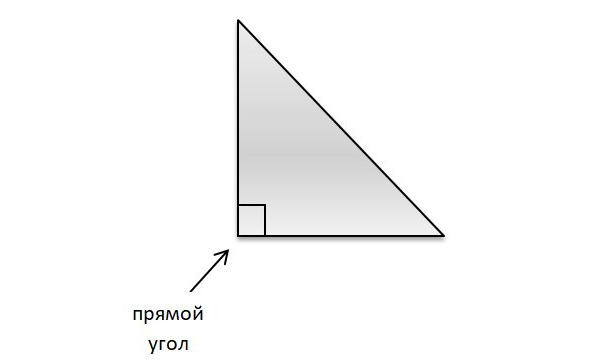
Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами. Это важный момент! Необходимо быстро и точно определять, какая из сторон является гипотенузой, а какие — катетами. Точно, потому что впереди теорема Пифагора!

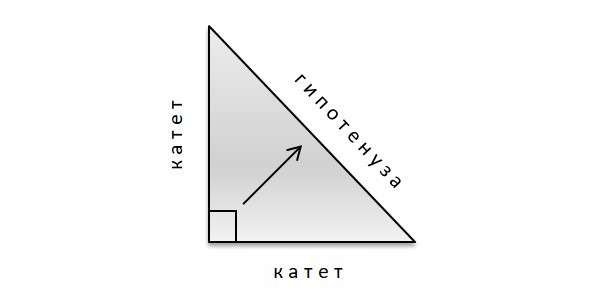
Итак, теперь вы точно знаете, что такое прямоугольный треугольник и как называются его стороны.

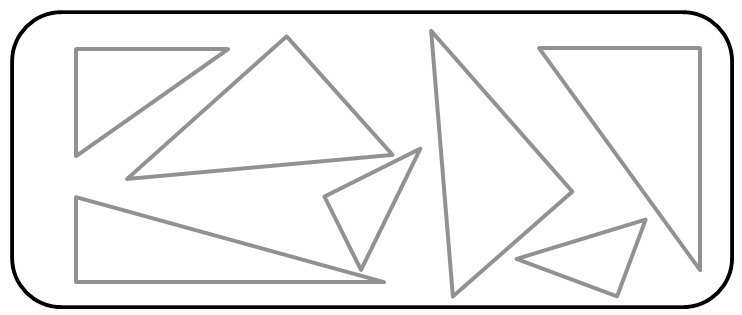
Домашнее задание: Потренируемся в определении сторон! Для каждого треугольника обозначь прямой угол и подпиши, где находится гипотенуза, а где — катеты.

Урок 2. Теорема Пифагора

Я как-то занималась с одной девочкой, которая каждый раз не могла вспомнить теорему Пифагора. То есть, все же есть те, кто не знают этой теоремы. Поэтому обязательно ее изучим!

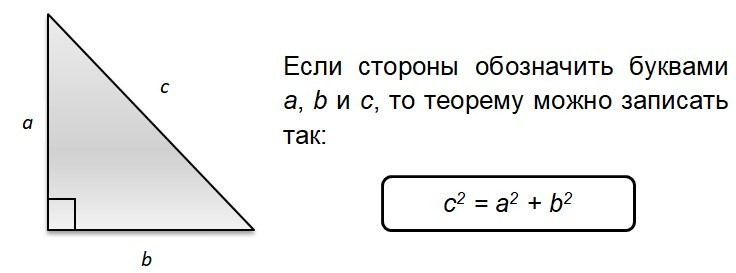
Пока все просто, правда? Разберем задачки из Открытого банка заданий ОГЭ ФИПИ.

Задание 1.

Катеты прямоугольного треугольника равны 20 и 21. Найдите гипотенузу этого треугольника.

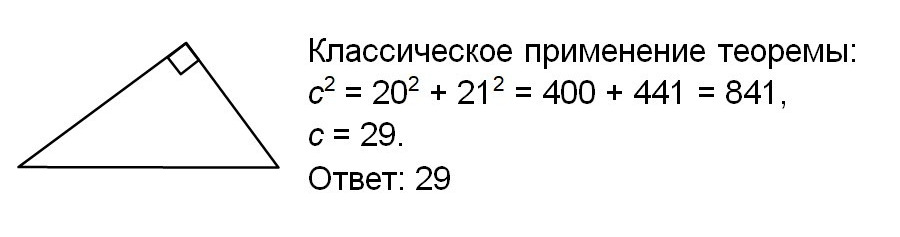
Задание 2.

В прямоугольном треугольнике катет и гипотенуза равны 8 и 17 соответственно. Найдите другой катет этого треугольника.

Задание 3.

Радиус вписанной в квадрат окружности равен. Найдите диагональ этого квадрата.

Итак, мы вспомнили теорему Пифагора. Отработайте  применение этой теоремы на задачке.

Домашнее задание

Урок 3. Теорема Пифагора

Да, снова теорема Пифагора. И здесь мы поговорим о вычислениях. Теорема требует много вычислительных действий: возвести числа в квадрат, сложить/вычесть, извлечь результат из корня. Можно проще? Можно!

Думаю, вам известно такое понятие «египетский треугольник». Про что это? Это прямоугольный треугольник со сторонами 3, 4 и 5.

Немного истории

Название это появилось уже в V веке до н.э., а сам треугольник широко применялся еще в Древнем Египте.

Как вы понимаете, в пространстве сложно отложить прямой угол, (в природе и так редко встретишь прямые линии, а уж тем более прямые углы), но египтяне изобрели интересный способ. Они брали веревку, отмеряли на ней узелками 12 частей, а потом складывали из нее треугольник, стороны которого равны 3, 4 и 5 частям соответственно. В этом треугольнике прямой угол получался сам собой! Имея такой инструмент, они могли с большой точностью строить свои сооружения, например, пирамиды. А также использовать его для разметки земли под сельскохозяйственные работы.

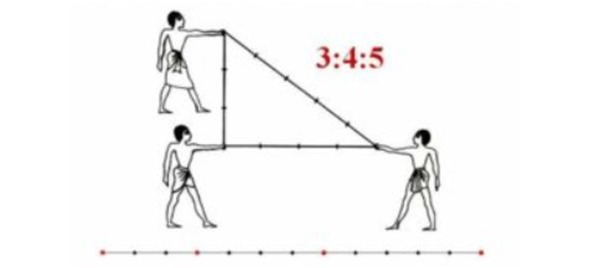
Как же этим треугольником пользоваться нам с вами?

Если в задаче вам попались данные числа, то считать совсем не придется! Например, «Катеты прямоугольного треугольника равны 3 и 4. Найдите гипотенузу». Ответ даем моментально: гипотенуза равна 5.

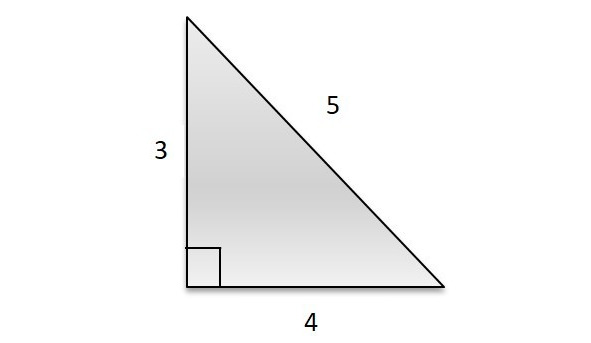
Но! Давать моментальные ответы можно не только с этими числами. Давайте увеличим катеты этого треугольника ровно в два раза: 6 и 8. Чему будет равна гипотенуза? Правильно, 10. А если увеличим в три раза: 9 и 12? Ответ у вас уже готов: 5 умножаем на 3, ответ 15. Просто? Просто!

Потренируйтесь!

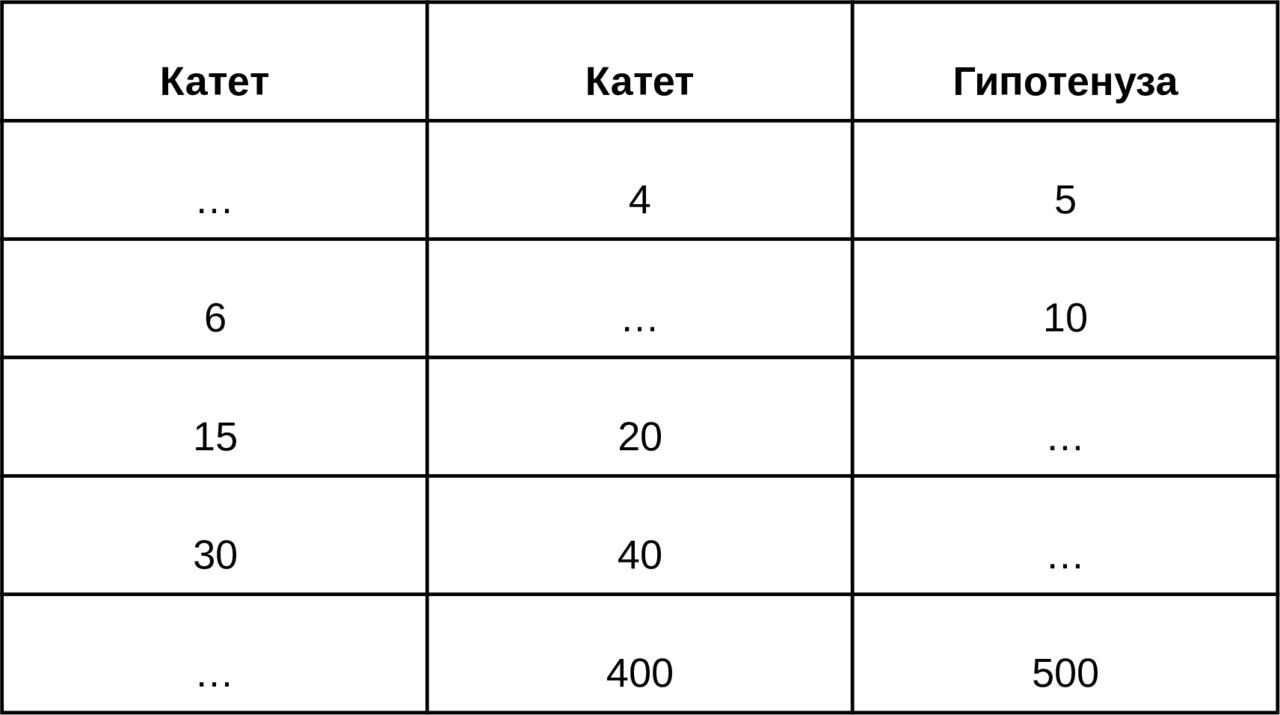
Но и это еще не все! Есть и другие «пифагоровы тройки» целых чисел, которые дает теорема Пифагора. Например, в заданиях прошлого урока мы встретили тройку 20, 21, 29 или 8, 15, 17. Сколько их? Много. Но все они нам не нужны. Мы с вами запомним наиболее часто встречающиеся:

Итак, вы научились быстро считать теорему Пифагора с известными тройками целых чисел.

Домашнее задание

Выучите перечисленные тройки чисел, тем самым сильно облегчите себе вычисления во многих задачах (а теорема Пифагора ох как часто встречается! До 11 класса, как минимум!).

Урок 4. Высота в прямоугольном треугольнике

Вам не терпится узнать, когда же начнется тригонометрия с синусами и косинусами? Скоро. В следующем уроке. А сейчас давайте очень коротко разберем еще один важный элемент прямоугольного треугольника — высоту, опущенную из прямого угла.

Что нужно про эту высоту знать? То, что она дает равные углы в полученных треугольниках, на которые разделила данный треугольник! Я отметила равные углы одинаковыми дугами:

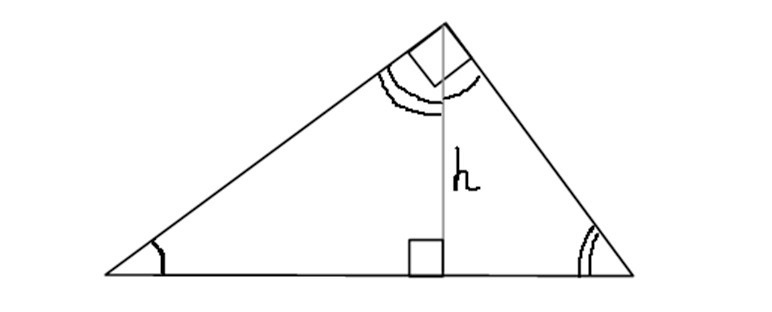
Вы узнали о равных углах в новых треугольниках, полученных с помощью высоты. Запомните это равенство, оно вам пригодится при решении задач.

Домашнее задание

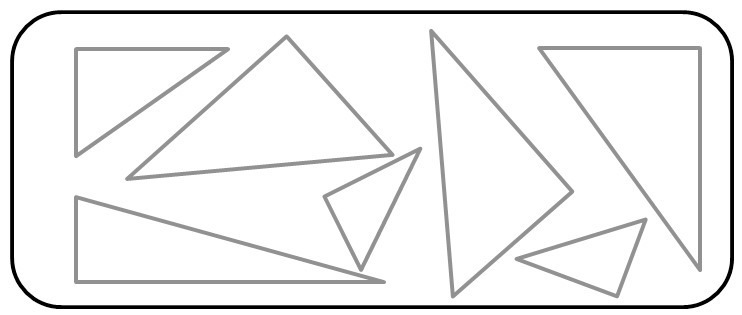
Проведите высоты в данных треугольниках и обозначьте равные углы:

Урок 5. Соотношения между сторонами и углами прямоугольного треугольника

Ура! Тригонометрия!

Начнем сразу с определений.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Что сие означает? Разберемся.

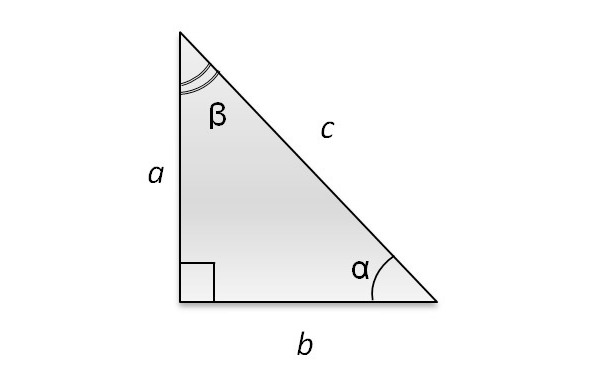
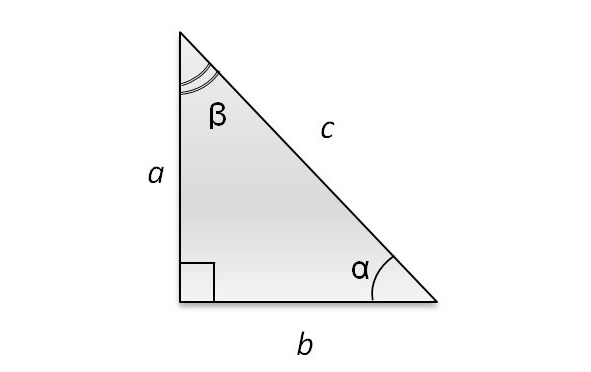
Во-первых, речь идет только об острых углах треугольника. В нашем треугольнике это углы α и β.

Во-вторых, отношение — это действие деления, т.е. катет нужно разделить на гипотенузу.

В-третьих, противолежащий катет — это катет, который находится напротив угла, синус которого мы ищем (для угла α — это катет a, для угла β — катет b).

Если записать в наших обозначениях, то выглядеть будет так:

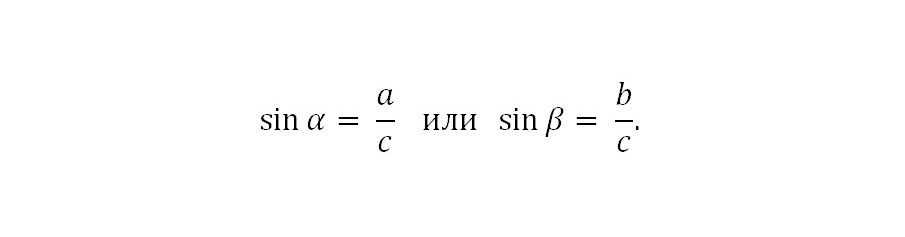
Ныряем в Открытый банк заданий ОГЭ и разберем еще несколько задачек.

Задание 1.

В треугольнике АВС угол С равен 90°, АС = 6, АВ = 10. Найдите sin В.

Задание 2.

В треугольнике АВС угол С равен 90°, sin В = 4/15, АВ = 45. Найдите АС.

Несложно, правда?

Перейдем к косинусу.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

«Во-первых» и «во-вторых» читаем у синуса.

В-третьих, прилежащий катет — это катет, который образует угол, косинус которого находим (для угла α — это катет b, для угла β — катет a).

Если записать в наших обозначениях, то выглядеть будет так: