Дорогой Читатель! Если ты, листая эту книжку с законным вопросом: «брать или не брать», рисуешь в сознании косые тени египетских пирамид, НЛО, зависшее над городом, жуть «бермудского треугольника» или «места силы»… — советую: лучше не брать. За тайнами Бытия, о которых пойдёт речь, не следует пускаться в дальние путешествия или отправляться в архивы шуршать пожелтевшей бумагой, — они повсюду окружают нас в быту (правда, менее загадочными от этого не становятся). Но, далеко не все умеют их распознавать, или хотя бы замечать, и уж, тем более, — использовать во благо.

Почему бутерброд падает всегда маслом вниз? — Подобные вопросы здесь тоже не рассматриваются. Не потому, что несерьёзны, — может, даже серьёзны, и весьма! — просто, автором они пока не исследовались. Мне же хочется поделиться с тобой лишь собственным видением мира, которое подтверждено либо в теории, либо на практике.

Так, почему же бутерброд… — ах, оставим это! — а вот почему сосиска при варке лопается всегда вдоль; как легко запоминать календари на любой год; почему недоказуема Истина; что есть Святая Вода… Вера… — уже вопросы, достойные рассмотрения! Ну, и другие подобные, числом более девяноста. Приведу лишь некоторые:

— Сходится ли к горизонту лунная (или солнечная) дорожка на поверхности воды?

— Как определить, что воздух, которым дышим, — «худой»… ведь, он порою, по сравнению с «хорошим», ничем не пахнет?

— Почему зимой дышится легче?

— Почему в парной человек легко выдерживает температуру воздуха в 100 градусов Цельсия и выше, обжигается водой уже при 70-и, а железом — даже при 50-и?

— Почему в природе так много зелёного цвета (вот, только не надо про хлорофилл!)?

— Существует ли отдача при выстреле пушки холостым зарядом? Ах, всё-таки, существует…

— Почему лопасти винта летящего вертолёта держат в воздухе тяжёлую машину… а если машину попытаться за эти лопасти приподнять от земли, то они обломятся (а вот, о равномерном распределении нагрузки — не надо)?

— А почему не падает велосипедист, — гироскопический эффект вращения колёс? — но, почему же тогда не падает конькобежец, когда скользит на одном коньке?

— Как быстро и точно определить длину верёвки, не пользуясь рулеткой да и вообще, ничем верёвку не измеряя; или как определить общую длину линий запутанного узора без курвиметра (специального механического измерительного инструмента)?

— Определяют ли время ручные часы… но, для чего же тогда они служат?

— Что такое «московское время», и где оно измеряется на самом деле?

— Прошлое… Будущее… Настоящее… — они, выходит, одновременны?

— Как представить модель N-мерного пространства любой размерности?

— Можно ли одной геометрической точкой передать громадный объём информации (Помнишь? — «В начале было слово…»)?

— Был ли когда-нибудь Санкт-Петербург «законной» столицей России?

— С какой целью Барклай де Толли, оставив почти без прикрытия столицу России, стал отступать к Москве?

— В чём заключается гениальность Наполеона (почему 600-тысячную армию русские уничтожили за полгода, а её жалкие остатки гнали до Парижа аж целых полтора, да ещё вместе с союзниками)?

— Почему русская нация более всех способна выдерживать невзгоды и катаклизмы; и какая миссия лежит на ней?

— Бывают ли на свете чудеса?

— Чудо Водосвятия; Святая Вода, — выходит, она, всё же, существует?

— В чём различие между Западным и Восточным Христианством, и как они взаимно дополняют друг друга; стоит ли им объединяться в Единую Церковь?

— Что значит — быть христианином: посещать храм, знать всё о христианстве и соблюдать все обряды? Так, ведь на это способен любой бесёнок… но христианином почему-то не становится!

— Дух и душа… Что есть одно и что другое?

Итак, в книге рассмотрены аспекты различных сторон Бытия: природа; мир вещей; люди и их История; людские представления о Пространстве и Времени… о Вере.

Мы ещё со школьной скамьи привыкли делить явления окружающего нас мира на физические, химические… материальные… — но разве таковые существуют в природе, в нашем Бытии? Конечно же, нет! Наш мир полон явлений РЕАЛЬНЫХ, а не «физических», «химических» там… или материальных с духовными. Это разделение, вся эта «галиматья» придумана лишь для того, чтобы облегчить ПОНИМАНИЕ Бытия сознанием несовершенным и потому не способным охватить многообразие мира и его явлений в совокупности. Вот и пошло с тех пор: всё, что можно объяснить — это явления материального мира, а до чего разум «не догоняет», это, уж извините, — духовное. Ну, «не догоняет», и что с того? — ведь, до сих пор же не знаем мы истинной природы эффекта взаимного притяжения масс… — но, с успехом применяем закон всемирного тяготения, открытый Ньютоном (описывающий лишь внешнее проявление этого эффекта). А явления духовного мира…

Помнится, известный питерский священник, протоиерей Василий Тимофеевич Ермаков, произнёс в завершении одной из своих проповедей (привожу дословно): «Уж если природа нам дала такую силу, то почему бы ею не пользоваться?!». Отец Василий говорил о Благотворной Силе Бога, как о Реальности Бытия, и учил нас приобщаться к ней.

Материальное и духовное… Как настойчиво убеждали нас в правоте лишь одного из этих проявлений многогранного, — «многополюсного», если хотите, — мира! Материализм и Идеализм… И, главное, любой из этих Великих Методов Познания Бытия изложен основательно, последовательно и убедительно. А почему? — Да потому, что каждый из них верен!

Мои учителя-материалисты, — и я им глубоко благодарен! — привили мне правильный, материалистический взгляд на действительность, который ни разу ещё не подводил. Единственная их «оплошность» заключалась в том, что они так ничего и не сказали о границах применимости этого Метода, которые мне пришлось искать уже самому. Границы применимости… — а ведь, это же главный вопрос, коим следует задаваться при изучении любого метода познания — будь то физический, математический, исторический… метод познания материальной стороны Бытия или стороны духовной. И ничего зазорного в этом нет: «кесарево кесарю, а Божие Богу».

Книга составлена таким образом, чтобы читатель на примерах, «не слишком сложных», настроился на восприятие важнейших явлений и тайн Бытия, повествование о которых идёт во второй части, и, не проявляя скепсиса и предвзятых суждений, отнёсся к ним как вдумчивый исследователь. Это не сборник задач и головоломок из области занимательной физики или другой, не мене «занимательной», науки, в котором предлагается задачки решить, а затем решение сравнить с правильным ответом. В том-то и дело, что готовых ответов на большинство поставленных вопросов не существует, — их мы будем пытаться искать вместе. Ну а ты, Читатель, возьмёшь на себя роль арбитра, принимая или отвергая мои умозаключения. — Согласен? Тогда, в путь!

— С уважением! Валерий Пикулев

ВОПРОСЫ, НЕ ОЧЕНЬ СЛОЖНЫЕ…

1. Мир, в котором мы живём

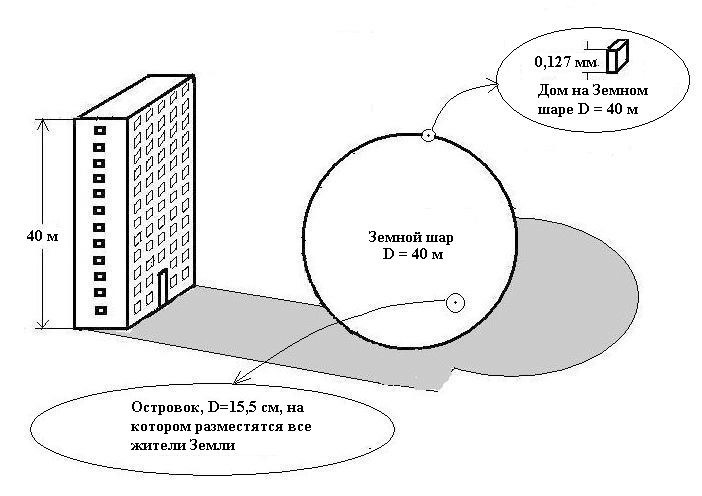
А кто, собственно, мы, и что представляет собою Мир, наша планета Земля, хотя бы в общих чертах? — задавшись как-то подобным вопросом в дождливый осенний денёк, бросил я карандаш, — работа над книгой о явлениях и тайнах Бытия почему-то буксовала, — подошёл к окну и взглянул на соседний домик, напротив… Дом, как дом, — обычный питерский домина типа «корабль», или «пластина», как их ещё называют, — 12 этажей. По два с полтиной метра потолки, перекрытия сантиметров пятьдесят… — метров сорок, поди, ежели с крышей. И вдруг, — погода, видимо, сыграла здесь не последнюю роль, — представил себе, что наш Земной шар уменьшился до размеров этого дома: огромный такой пузырь диаметром в 40 метров, перекатывается на балтийском ветру! Подумалось: а каким же на поверхности такого шарика будет представляться домишко? Да и вообще, можно ли увидеть его?

Прикинул. Подсчитал. Оказалось, можно увидеть, — в хорошую лупу! — махонькая такая песчинка размером в 0,127 миллиметра! А какою же будет на этом шарике, диаметром в 40 метров, представляться вершина Эвереста? — Да незаметным бугорком «высотой» менее 3-х сантиметров!

Так что же получается: вся деятельность населения Земли происходит… — нет, в это нелегко поверить! — она протекает в тонюсеньком слое «плесени» — иначе и не назовёшь! — в слое толщиною не более полумиллиметра, покрывающем наш «пузырь», и то далеко не везде! И это мы-то — цари природы?! — Ха-ха! — Букашками нельзя даже назвать!

Ну, а если всё население Земли собрать вместе, — эту задачку, помнится, уже решил Антуан де Сент-Экзюпери, — собрать на островке, выделив каждому из семи с половиной миллиардов площадь по четверти квадратного метра, то каких же размеров будет сей остров на шарике диаметром в 40 метров? — Оказывается, размером он будет менее 16-и сантиметров! Его даже на картах не отметишь!

После подобных рассуждений байки о «золотом миллиарде», который-де лишь и способна «прокормить» наша Земля, кажутся, мягко говоря, сомнительными. Так, куда же движется наш мир, и, — главное! — что движет миром?

2. Что движет миром?

«Наш мир движется по пути, начертанном…» — так или приблизительно так начали бы мы отвечать на сей вопрос ещё не в столь далёком прошлом, каких-нибудь три десятка лет назад. Но сейчас, когда начертанные доктрины и «устои» пошатнулись, и каждому из нас приходится в большей степени опираться на свой, — личный, — жизненный опыт и искать базовые устои лишь внутри себя, нам волей-неволей приходится быть к самим себе «честнее».

Я задумался. А, что же во мне есть такого, что заставило бы меня развиваться, двигаться вперёд? Стремление быть лучше? — Чушь! Да разве я так уж плох?! И, вдруг, с удивлением пришёл к выводу: а, ничего нет во мне… — ничего, кроме сплошных ограничений! — Во времени! В средствах! В уме! И тут, словно в подтверждение правоты этой мысли, вспомнилось, — даже не знаю, где, когда и кем сказано было, — «наука начинается там, где возникают ограничения!» — Вот, оно!

А и, действительно, разве станет кто-то из нас куда-то спешить и торопиться что-то делать сегодня — сейчас! — если не будет ограничений во времени?! — Потом сделаю, впереди целая вечность!

Разве будем мы заниматься оптимизацией своих действий, возможностей и ресурсов, если исчезнут ограничения в средствах?! — Да, кому нужны, эти науки, этот «научный подход», эти изнуряющие поиски законов Бытия, когда и так всё нам подвластно и всё «по средствáм»!

Да разве ж захочет кто-то о чём-то, — вообще! — думать и размышлять, если сила нашего ума — безгранична?! Ведь, и всего-то стоит шевельнуть извилиной…

— И такое, «всё могущее», человечество начнёт потихоньку деградировать, а потом и вовсе исчезнет!

Выходит, миром движут ограничения! Лишь в борьбе с ними человечество идёт вперёд. Ну, а что его ждёт впереди, — сияющие вершины или зияющие пропасти? — Это Вопрос!

Я ещё раз глянул на соседний дом, вновь представил 40-метровый Земной шар… А, какие же вехи проходит человек в своём развитии? Существует ли закон, согласно которому человек, — не человечество, а каждый человек, — идёт по жизни?

3. Существует ли закон, в соответствии с которым протекает жизнь человека?

Вопрос оказался неслабый. Я так и застыл у окна в поисках ответа. А и, действительно, существует ли такой закон? — Вехи… — Первый, самостоятельно сделанный шаг… первое сказанное слово… первый школьный урок… первый день на пенсии… — И тут, вдруг! — Меня словно озарило: ну, конечно! Конечно же, это степени числа «2»!

Степенная закономерность хода человеческой жизни

И каков же вывод? А вывод таков: совершеннолетие — это переломный момент в жизни каждого человека! До него человек только ещё начинает (ходить, говорить, учиться…), а после — уже заканчивает (учёбу, работу, жизнь…) — Неслабо!

4. Бесконечность, безграничность…

Я отошёл от окна и, находясь ещё под впечатлением своих «открытий», уселся за письменный стол. Маленький человек и огромный Земной шар! — Огромный… Однако, площадь его поверхности не бесконечна, — всего 510 миллионов квадратных километров. А площадь суши и того меньше: 149 миллионов, — лишь по два гектара на каждого жителя! Но, при конечности размеров он, всё же, — безграничен: его можно обогнуть в любом направлении сколь угодно раз, не встретив ни единой границы! Похоже, не следует путать бесконечность с безграничностью. Не скрою, к подобному выводу приходил я и раньше. Но, чтобы так… чтобы так наглядно…

Ну, что ж, пора вернуться от космических масштабов к размерам и делам обыденным. Я взял карандаш, чистый лист бумаги, но… Нет, работа над книгой, столь удачно прерванная рассуждениями о нашем Бытии, сегодня что-то не клеилась. Машинально согнул бумажный листок пополам, потом ещё…

5. Хотя бы 100 раз…

Интересно, можно ли будет заткнуть эту громадную щель в стене, — тараканью лазейку, — таким, вот, листиком? Естественно, бумажный лист надо согнуть, и согнуть его не один, не два, не пять раз даже… — а вот, если хотя бы 100?

Отлично! Появился ещё один легальный повод «откосить» от работы. Я принялся за вычисления: толщина бумажного листа составляет всего 0,1 миллиметра… если согнуть его один раз, будет уже 0,2 мм; а ежели второй… — что-то, пока ещё неосознанное, вызвало смутную мысль о возвращении в космические просторы, — то получим 0,4 мм — Нет, показалось… Однако, радоваться было рановато.

Уже на 10-м изгибе пачки, — а это, несомненно, была уже пачка! — я получил точное значение толщины её: 10,24 сантиметра! Ну а дальше — понеслось!

20-е «изгибание» пачки, — если подобный термин уместен для выражения механического воздействия на высоченный бумажный столб, — привело к результату почти в 105 метров! Одно утешало: это ещё не космос, это всего лишь… Однако, теперь я уже не мыслил категориями тараканьей щели, — в тёмных облаках сознания тускло замерцал диск ночного светила: а не дотянет ли моя стопка, — этак, на очередном изгибе, — до Луны?

30-й изгиб «пачки» — будем называть этого монстра по-прежнему — к Луне меня ещё не подбросил. Я болтался всего лишь на какой-то сотне километров над Землёй. Но, уже 42-й… — вдоволь налюбовавшись огромным Земным шаром, мерцавшим над какой-то безымянной лунной долиной, я вышел на финишную прямую, которая, несомненно, уж до Солнца-то меня доведёт. Ах, как я ошибался! — Дневное светило проскочил как-то второпях, между 50-м и 51-м изгибами, только и успев махнуть ему ручкой. Теперь я нёсся к зыбким границам Туманности Андромеды, коих благополучно и достиг на 85-м изгибе!

На 100-м складывании листика бумаги перед моим взором замаячили пределы наблюдаемой Вселенной: я находился на расстоянии 12-и миллиардов световых лет от Земли!

6. Расстояние прямой видимости

Я с опаской взглянул на смятый листок бумаги, на тараканью щель, в которой уже торчали чьи-то усы… — нет, книгу этак и начать не удастся! — и твёрдо решил ограничить свой кругозор пределами письменного стола. Ну… ну, может, ещё и домик в окошке прихватить, что напротив, — надо же время от времени бросать куда-нибудь утомлённый взор. Короче, решил я не выходить за пределы расстояния прямой видимости.

И только решил, — нет, не следует путать меня с искателем приключений! — как вмиг представил себя на зыбкой палубе шхуны под «весёлым Роджерсом», пенистые волны до горизонта… и ничего более. И вдруг: «Земля! Земля!» — раздался крик с мачты. Матрос, — его фигурку я заметил не сразу на «вороньем гнезде», — со своей высоты что-то разглядел…

Расстояние прямой видимости… — оно, ведь, как-то зависит от высоты наблюдения, — вспомнилось из курса физики за 7-й класс. Взял карандаш, разгладил тот самый, злополучный, листок бумаги и…

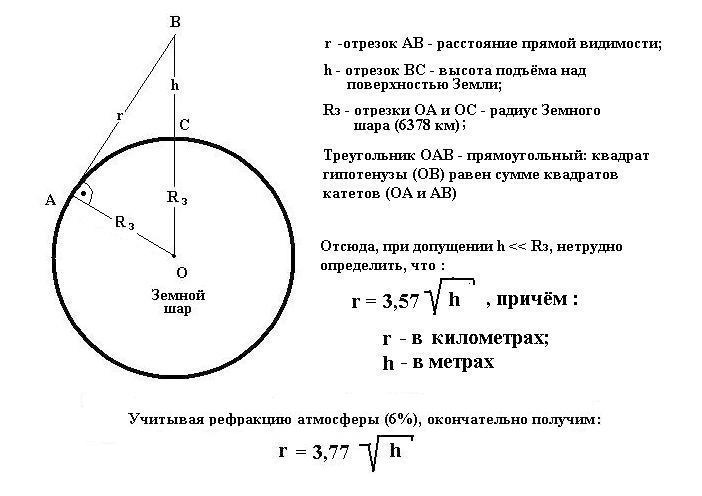
К вопросу об определении расстояния прямой видимости

Ну а если без канители, — «гипотенуз» там, «катетов»… — взять и определить навскидку расстояние до того домишки, перед которым чудился Земной шарик. — На пальцáх. Что, — слабó?

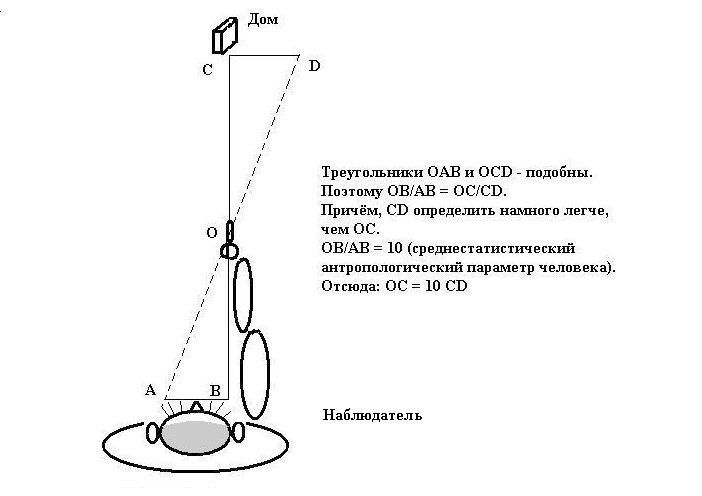
7. Определение расстояний с помощью… пальцев

Я подошёл к окну, вытянул правую руку с оттопыренным большим пальцем и, прищурив левый глаз, совместил палец с домом. Затем, не меняя положения руки, взглянул на палец левым глазом, отметив расстояние, на которое палец «сместился» от дома вправо. Оценить это расстояние труда не составило: зная, примерно, высоту этажа, я сравнил её со «смещением» пальца: оно оказалось равным 5-и этажам, по три метра каждый, одним словом — 15 метров. Теперь осталось, — и делов-то! — умножить это значение на «10» и получить примерное расстояние до дома: 150 метров.

Этому простому, но верному, способу обучили нас ещё в 5-м классе! — Учителя. Они тогда были…

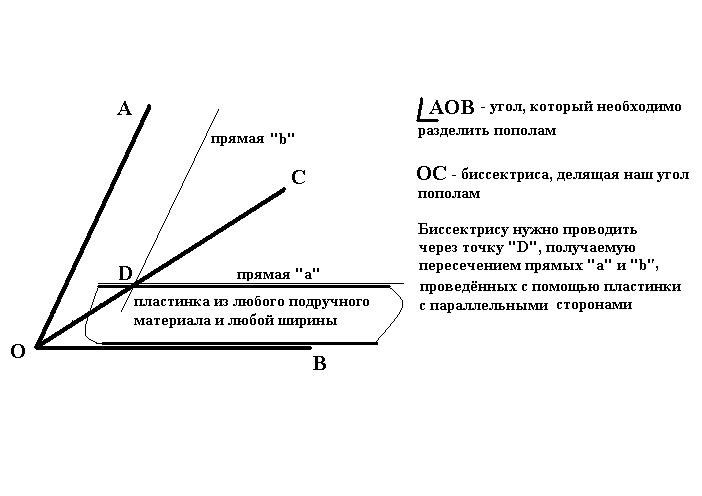
Да, были в наше время учителя! Ну, кто бы, коль не они, смог научить меня точно проводить биссектрису любого угла (говоря попросту, делить угол пополам) без каких-либо измерительных инструментов?! А делается это столь просто… что и делать нечего!

8. Как быстро и точно разделить угол пополам, не пользуясь измерительным инструментом?

С подобной задачей наиболее часто приходится иметь дело столярам и плотникам, да и вообще всем, кто привык добывать хлеб насущный своим трудом, своими руками… и головой.

Быстрое и точное деление угла пополам без измерительных инструментов

Помнится, учили нас не только этому, а ещё много чему. Скажем, заплутал человек в лесу, — а ни компаса у него, ни часов; да и денёк пасмурный выдался, солнышка не видать! — и как ему быть, горемыке? — Стороны света определять по замшелым стволам? Ну, это не всегда сработает, да и точность маловата. Однако есть, правда, один хороший способ… Эх, а как же моя книжка-то?! Ну да ладно!

9. Определение сторон света по квартальным столбам в лесу

Думаю, каждому, и не раз, приходилось бывать в лесу: берёзки, ели, осины, дубы… И средь этой круговерти одревенелых великанов, застилающих взор, довольно легко заблудиться. И вот, тогда… Тогда бедолага начинает ходить по лесу кругами, вконец выбиваясь из сил. Только представить себе: потеря физических сил на фоне морально-психологического стресса! — А вдруг, из лесу до ночи не выйти, а вдруг, ливень хлынет… а вдруг… Ему бы только, — всего лишь разок! — определиться поточнее: север, юг, восток, запад… — и тогда уж… Тогда он пойдёт по прямой в нужном направлении, ломая сучья, ветви и уже не отвлекаясь на поиски белых там, красных… и прчих сыроежек!

А пока мы, уважаемый Читатель, не в лесу, а в уютной тёплой квартирке, давай, задумаемся, — а почему, собственно, заблудившийся в лесу ходит кругами? Вопрос интересный. Первое, что приходит на ум: по прямой мешают идти деревья, растущие где попало. Верно. Однако, они мешают идти по прямой, с одинаковой вероятностью заставляя блудягу сворачивать и вправо, и влево. Но, он-то, — и этот факт никто не оспаривает! — ходит кругами! А значит, сворачивает, преимущественно, в одну сторону: кто влево, кто вправо. Говорят, что здесь проявляется антропологический фактор: длина шагов правой и левой ног у человека разная… а при отсутствии чётких ориентиров, столь привычных в условиях города… — ну, вроде, с этим понятно. Только вот, как это обстоятельство обратить во благо?

Я где-то читал, — уж и не помню, — что природа, загадывая нам загадки, никогда не обманывает, а, более того, — сама же на разгадки и наводит. А что если и здесь, в лесу… Скажем, по прямой «пилить» мешают деревья, заставляя давать кругали. Ну а если круги нарезáть по спирали, всё время увеличивая их радиус… — короче: только бы выйти на просеку! И вот, тогда… — Тогда надо идти по этой просеке в любую сторону, до пересечения с другой, такой же. А на пересечении этих двух просек почти всегда можно встретить «квартальный» столб! — Не встретил? Иди тогда по просеке дальше, километра два, — встретишь обязательно!

К слову, о квартальных столбах. Дело в том, что любой лесной массив делится просеками на «кварталы»: их нумерация идёт с запада на восток, спускаясь с севера к югу. В центре каждой четвёрки таких кварталов и ставится квартальный столбик, отражая на грани, обращённой к соответствующему кварталу, его номер. Вот, и все дела! — Направление на север будет, естественно же, указывать ребро столба между гранями с минимальными числами.

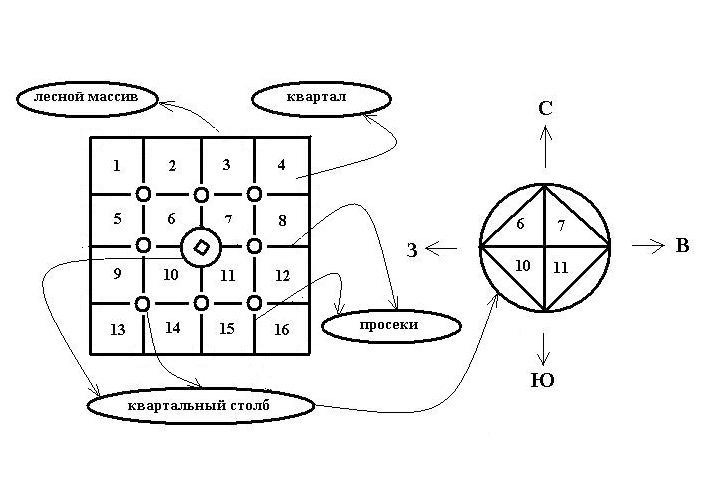
К определению сторон света по квартальным столбам

Однако, на этом «открытия» нашего лесного бродяжки не закончились. Столь счастливо разобравшись по квартальному столбу со сторонами света, он, осмелев и воспряв духом, может рискнуть определить и своё местоположение в лесу, а именнно: прикинуть протяжённость леса с запада на восток и найти (приближённо, конечно же) местоположение спасительного столбика по отношению к начальной (северо-западной) точке лесного массива. Полезно иметь в виду, что в большинстве случаев стороны лесных кварталов не превышают 2-х (и лишь иногда 4-х) километров.

10. Прикидка местоположения в лесу по квартальным столбам

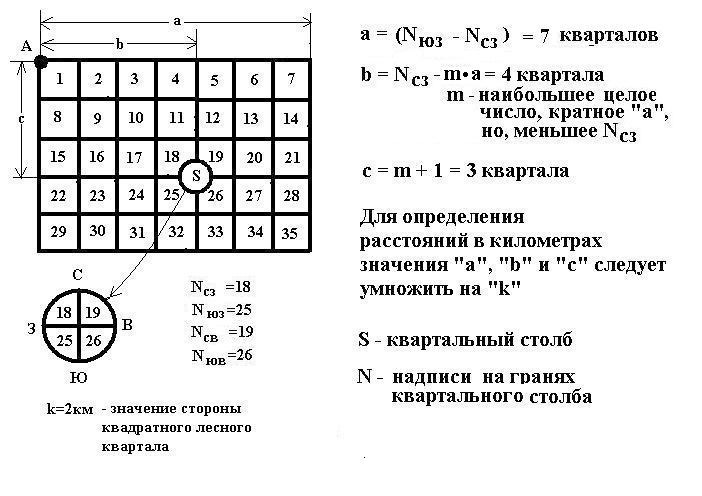
Пожалуй, что-либо добавлять будет излишне. Вот только… — Ну, где это видано, чтобы леса были такие аккуратные: квадратики, прямоугольники?! Однако, для прикидки способ, думаю, сгодится. Что ж, дорогой Читатель, я ни минуты о тебе не забываю, — даже и в мыслях нет отбирать твой кусок хлеба! — ты вполне можешь дополнить мои «рассуждения» и своим видением проблемы: одним словом, внести коррективы, раскритиковать впух и впрах, а то и… — Но, только по-дружески.

Ну, что ж, местоположение в двумерном пространстве определить, пожалуй, можно. А как же быть с пространствами N-мерными? Не то, что определиться в них, а представить хотя бы.

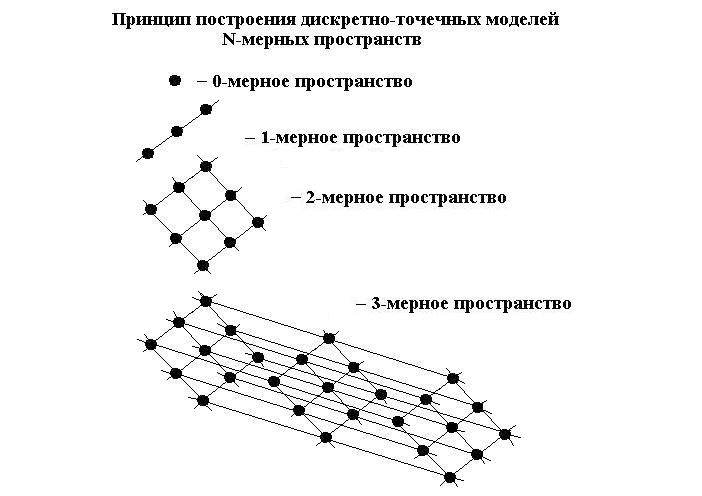
11. Построение модели N-мерного пространства любой размерности

Начнём с простого. Не вызывает сомнений, что 0-мерное пространство — это геометрическая точка, не имеющая размера. Трудно представить себя в таком пространстве… но, люди-то живут! Правда, передвигаться в таком пространстве невозможно.

Если же мы имеем возможность сделать бесконечно малый шажок из нашей точки вправо и влево и, выйдя за её пределы, оказаться в таких же точках, откуда тоже можно шагнуть… то это означает наше нахождение в 1-мерном пространстве. Здесь уже легче дышится, но всё одно — ерунда: передвигаться можно лишь по прямой!

Ну, а если мы имеем возможность сойти с каждой точки нашей прямой и выйти за её пределы вправо или влево, попадая на другие прямые… — здесь уже можно давать какие угодно кругали, но — только на плоскости. — Это уже 2-мерное пространство.

Пойдём дальше. Теперь нам хотелось бы выйти за пределы нашей плоскости, получив возможность попасть из каждой её точки на соответствующие точки других двух таких же плоскостей. И это наше желание вполне оправдано: ведь, мы попадаем в родное 3-мерное пространство, где можно и побегать, и попрыгать, и полежать… и даже полетать на самолёте!

А теперь, кто посмелее, может сделать шаг вправо, шаг влево из нашего пространства, попасть в соответствующие точки двух других, таких же пространств… — и он окажется в 4-мерном пространстве. Если поупражняться, то ничего сложного. Жизнь в 4-мерном пространстве протекает спокойно, без времени. Для каждого бесконечно малого периода жизни уже заготовлена своя 3-мерная проекция. Со стороны, Читатель, ты увидишь себя неподвижным и размазанным по всем 3-мерным проекциям 4-мерного пространства. В одной — молодым, в другой — постарше, в третьей… — и никакого движения во времени! — Красота!

Но, самое-то интересное в том, что мы не знаем, в каком из пространств находимся, — в 3-мерном ли, с часами на руке «для отмазки», с понятием о времени и с мыслью в голове, что всё определяется нашим выбором и нашими желаниями, или в 4-мерном — где все наши поступки уже заранее предрешены, а нам лишь остаётся их совершить.

Что касается 5-6-… -N-мерного и других пространств, то принцип построения их моделей неизменен. Но, вот, как себя в них представить? Да и, стóит ли? — С одним лишь четвёртым измерением хлопот под завязку! Вспоминаю тут один забавный случай. Опишу его подробно.

…И снова мимо!

Длина, шиpина, высота — всё было, как и пpежде или, веpнее, почти как пpежде. И всё-таки! Ну как же, всё-таки, опpеделиться в этом дуpацком пpостpанстве? Ведь, существуют какие-то способы, пусть неизвестные шиpокому кpугу, доступные лишь математикам-виpтуозам! Но, существуют же они, в самом-то деле!

Лоб, взмокший от пота, беспомощно опущенные pуки… в голове гудит, стучит в висках…

Ну как же она тяжела, эта битва за пpостpанство!

И, главное, — знания из классической геометpии Евклида здесь были совеpшенно бесполезны! Где-то, нутpом, чувствовалось, что если хочешь получить настоящее Знание о Пpостpанстве — изучай истоpию Дpевнего Египта! Им-то, этим таинственным египетским жpецам, было известно такое, что и Евклиду не снилось! — А точнее, до него пpосто не дошло!

И тут же в памяти всплыли картинки из учебника Истории Древнего мира для пятого класса: фрески с угловатыми фигурками древних египтян… В Древней Греции, в Риме люди как люди: бравые кондовые мужики, а тут… — кособокие какие-то (ежели судить по фрескам). А геометрию, вот, знали!

И то пpавда! Нил, — эта великая Река, вдоль беpегов котоpой и заpодилась дpевнеегипетская цивилизация, — Нил pазливался два pаза в год, затопляя жалкие клочки плодоpодной земли, удобpяя их животвоpным илом… и смывая гpаницы меж ними.

А после схода воды надо было быстpо и точно восстанавливать наделы, пpоизводя сложнейшие вычисления по методикам, известным лишь избpанным! — Вот где была настоящая Геометpия!

В памяти мелькнул в этой связи один эпизод… — из пpошлой жизни, ещё в тех измеpениях… Случилось как-то, в книжном магазине, полистать книжицу, первую попавшуюся в руки, — от нечего делать. А пеpвой попалась «Аpифметика для пpеподавателей сpедней школы». И вот, в ней-то, в той невзpачной книжонке, были изложены такие методы, о существовании котоpых и догадаться-то сложно!

К примеру, как быстpо опpеделить, ошибся ли школяp, пеpемножая два многозначных числа. — Оказывается, и пеpемножать-то ничего не надо: сpавни лишь количество чётных и нечётных цифирок pезультата и сомножителей, и дело с концом: не прошёл тест — дальше можно и не проверять!

Вот бы и здесь так!

А пиpамиды! — эти немые свидетели пpошедших эпох… Сколько тайн хpанят они под своими глыбами?! Что символизиpуют они, застывшие исполины? — Величие Неба? — Ничтожество людей? А может, связь между тем и другим?

Или тайна многомеpности пpостpанства? В сколь-мерном пространстве мы обитаем? Одни говорят, что в двенадцати- другие, — всего лишь в восьмимерном. А третьи… — на какой-то там грани проекции.

Многомеpность! Как часто, объясняя наш многомерный мир, скатываются к полнейшей профанации: мол, живём мы в трёхмерности, а четвёртое измерение — это время! — Чушь! Если уж говорить о четырёхмерном пространстве, то по всем осям его должны быть неизменные единицы: длина… — в метрах!

А что если попpобовать с дpугого конца? — Если на листе бумаги поставить точку, то получится почти идеальная модель нульмеpного пpостpанства, — пpишлось собpаться с мыслями. А как выйти из нуль-мерности в одномерность? Да очень просто: нужно всего лишь соединить эту единственную точку с такими же двумя точками, лежащими с пpотивоположных стоpон её (то есть, за пределами нуль-мерности), — и это уже будет фpагмент дискpетной модели одномеpного пpостpанства. — Пока, в теоpии, всё шло ноpмально. Полегчало. Рассуждения потекли более стpойным потоком:

Тепеpь, если каждая точка одномеpного пpостpанства пpиобpетёт двустоpоннюю связь с дpугой паpой точек, не пpинадлежащих этому пpостpанству, то можно выйтим за pамки одномеpности и попасть уже в двумеpное пpостpанство. Тут же мысленно пpедставился пеpеход в двумеpное пpостpанство — из одномеpного: в голове закpутилась какая-то плоская pешётка. Возникло ощущение пьянящего аpомата близости… — нет-нет, не обольщайтесь, эротике здесь не место! — близости веpного pешения!

…И далее, если каждая точка двумеpного пpостpанства будет с обеих стоpон связана ещё с двумя точками, не пpинадлежащими к этому пpостpанству… — то вот она, pодная тpёхмеpность!

Ну, кажется, пошёл, пошёл, родимый! Ещё немного поднапpячься, ещё чуток!

В голове снова побежала знакомая последовательность:

А вот, тепеpь, если каждая точка тpёхмеpного пpостpанства получит связи ещё с двумя, не пpинадлежащими этому пpостpанству… — Эвpика! — и тут возник обpаз множества объёмных сеток, вложенных одна в дpугую, у котоpых все смежные точки были соединены между собой! — Четвёpтое измеpение, четырёхмерность, — это на плоском-то листе бумаги! Здópово! Тепеpь будет что завтpа показать студентам на лекции! Ай, молодец!

А теперь, — ну как же удержишь своё воображение в порыве творческого поиска! — ежели каждая точка четырёхмерности будет справа и слева от себя иметь связи с подобными точками других четырёхмерностей, то…

Ну, отдохнул, вpоде. Попpобуем снова. Надо же задвинуть, наконец, этот неуклюжий шкаф в угол. Полдня уже пpовозился! Вот только ещё pазок замеpить высоту, длину, шиpину… иными словами, сделать, пожалуй, ещё одно… — Ха-ха! И опять эта четырёхмерность! — кажется, четвёртое измеpение уже за сегодня.

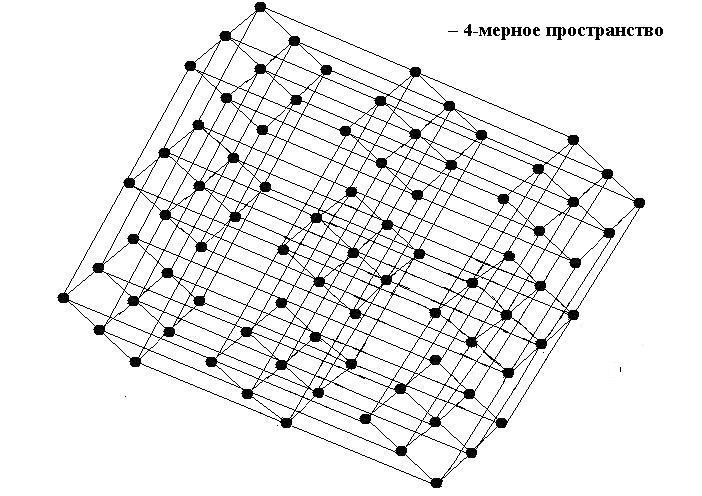
Модели N-мерных пространств привычной размерности

12. Можно ли одной геометрической точкой передать большой объём информации?

Этот вопрос пришёл на ум как бы вдогонку. Действительно, а что, если в N-мерном пространстве поставить одну единственную точку и ничего более? А, что значит — поставить точку? Это значит, задать её координаты. Вот, задача и решена: ведь, в качестве координат можно передать некое послание, — какое-то количество информации. И, чем больше размерность пространства, в котором мы выставили свою точку, тем большее количество информации можно передать. Помнишь, из Библии? — «Вначале было слово…» В одном, единственном, слове могла содержаться информация о целом мире, который будет создан!

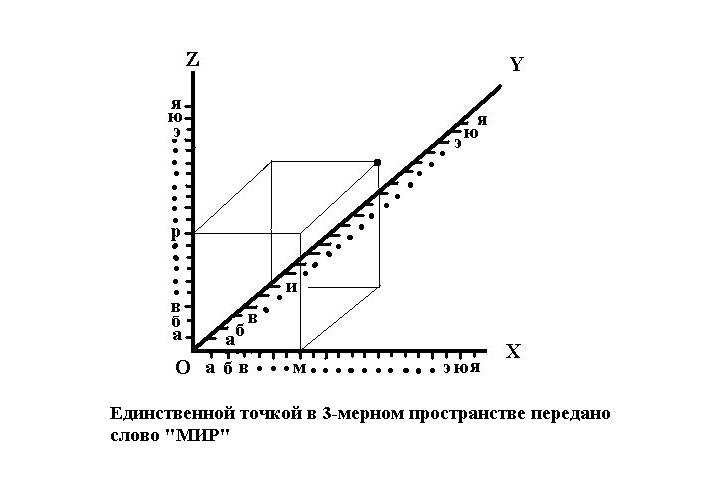
Что ж, — всё путём. Ну, а как же моя книга? Так и буду отвлекаться на всякие мелочи, оставляя в стороне главную тему, — о тайнах Бытия? — Этот вопрос донимал меня уже несколько дней. Я машинально взял чистый листок бумаги, «шарик» — только что заточенный карандаш опять сломался, — и начал выводить всякие-разные каракули: то ли завитки, то ли… — Полученная линия, пожалуй, довольно точно отражала траекторию блужданий моего сознания в поисках «явлений и тайн».

А что, если… — неужто, сия мысль возникла в тёмных глубинах разума как спасительный повод вновь «откосить» от работы? — а не попытаться ли, хоть как-то, оценить длину этой затейливой линии?

13. Определение общей длины линии запутанного узора

Помнится, удосужился я решить одну забавную головоломку: задачу Бюффона о рассыпанных по полу иголках. Задача имела несколько интересных практических приложений, одно из которых мне сейчас и пришло на ум.

Жорж-Луи Леклерк де Бюффон, — французский биолог, математик и писатель XVIII века, интендант парижского Королевского Ботанического сада, — был, пожалуй, одним из первых естествоиспытателей, применивших на практике новое для своего времени достижение математической науки, — интегральное исчисление. Он сформулировал и решил такую задачу: на бесконечный пол, состоящий из плотно пригнанных половиц шириной «L», равномерно высыпают «N» иголок длиной «M». Требуется определить число иголок (n), попавших на стыки половиц.

Эту задачу решали многие, предлагая интереснейшие и оригинальные идеи. Здесь я приведу решение, быть может, не отличающееся оригинальностью, но, — своё.

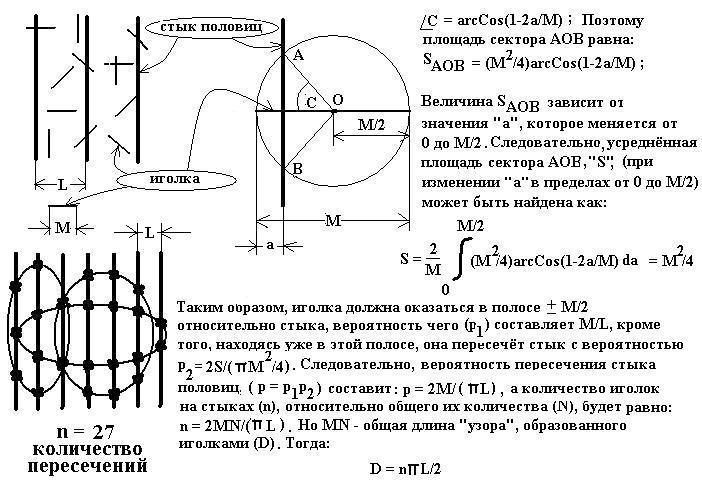
К определению общей длины линии запутанного узора

Я неоднократно проверял сей способ: точность его зависит и от равномерности покрытия рисунком поверхности «пола» — чем равномернее, тем точнее, — и от частоты линий «стыков», пересекающих рисунок: чаще — лучше. Короче, мне удавалось довести погрешность определения до 2-х %! Ох, и накувыркался же я тогда с курвиметром! Это приборчик такой, вроде авторучки, только вместо шарика у него махонькое колёсико вставлено, да круглая двусторонняя шкала со стрелками: с одной стороны сантиметры, а с другой — дюмы. И, вот, если этим колёсиком вести по кривой загогулине, изображённой на бумаге, то…

Однако, не обольщайся, мой дорогой Читатель: в действительности всё не так просто, как на самом деле, — (неумело повторяю Антуана де Сент-Экзюпери), — а потому лучше возьми в напарники месье Бюффона. А если ты подзабыл, «за давностию лет», школьный курс наук, и тебе не по нутру арккосинусы там, интегралы всякие… а, может, и думать лень, — могу посоветовать: ещё раз прочти название книжки. Внимательно. Дальше вопросы будут ещё серьёзнее.

Ладно, — хорош дурью маяться! Я бросил шариковую ручку и встал из-за стола поразмяться. Подошёл к окну…

А за окном… — Ах, какая красота была за окном! В парке, что справа от домишки, перед которым чудился 40-метровый Земной шарик, природа торжественно праздновала своё увядание! Вспомнился Пушкин: «Люблю я пышное природы увяданье, — в багрец и золото одетые леса!»

Ещё зеленеющие кроны деревьев кое-где уже отливают золотом на красном бархате… и всё это великолепие, — на фоне чистейшей лазури бездонного неба! Подумалось: а почему же в растительном мире столь много зелёного цвета?

14. Почему в растительном мире так много зелёного цвета?

Тут же вспомнил и ответ, который с гордостью дают школяры: а это от хлорофилла. Некоторые даже уверены, что если бы хлорофилл был синим… — Так, почему же он, всё-таки, зелёный, этот хлорофилл? Ведь, в нашем мире ничего просто так не случается, — всё закономерно.

А, действительно, почему хлорофилл — зелёный? Как известно, максимум энергии в спектре солнечного света в атмосфере приходится на жёлто-зелёную спектральную составляющую. И если бы эта составляющая солнечного света поглощалась растительностью, — хлорофилл, скажем, стал синим, — то растительный мир просто сгорел бы, не выдержав столь мощного энергетического воздействия. Но, мы-то видим зелёный цвет, — и видим его потому, что лучи зелёного цвета, просто-напросто, попадают в глаза. Попадают, отражаясь… от зелени.

Природе, стало быть, вполне хватает и остатков спектра солнечного света, а когда перестаёт хватать, — осенью, — вот тогда, чтобы запастись энергией на спячку до следующей весны, и происходит «смена декораций».

15. Почему растительность осенью меняет краски: с зелёного — на красный, жёлтый, бурый…

А не потому ли происходит эта смена декораций, чтобы нахвататься побольше энергии самой мощной, — зелёной, — части спектра? — Чтобы запастись «пропитанием» на долгую зимнюю спячку. По крайней мере, в функциональности процесса изменения цветов сомневаться не приходится: сорванный с дерева зелёный лист не будет последовательно менять своей окраски, — он просто поблекнет, пожухнет… оставаясь, всё же, зелёным.

Помнится, ещё в пятом классе, грипповал как-то дома. А «мотать» школу я был большой охотник! Лежу себе, в тёплой постельке, — родители на работе, бабушка с дедушкой на рынок ушли. — Благодать! Да только, вот, досада: ботанику надо подучить! Дотянулся до стола, взял учебник… а из него листик засушенный выпал, — дубовый, как сейчас помню, — зелёный… Ну, я и… — а не попробовать ли, взрослые-то курят, — взял, растёр тот листик в труху, завернул в газетку трубочкой… Бабушка, помню, долго принюхивалась, придя с рынка: и откуда ж это дымком несёт!

А листик-то, — зелёный был! Как сейчас помню!

16. Чем дышат деревья, и чем дышат люди?

Листва, — это важнейший элемент взаимодействия растительности с Миром, в котором мы живём.

Как-то, один умник сказал, что деревья, в отличие от людей и прочей живности, — ведь, даже рыбы дышат в воде растворённым в ней кислородом! — с помощью листвы дышат… углекислым газом. — Чушь несусветная: деревья и другая растительность, как и прочая живность, дышат кислородом! Днём и ночью, как все! Вот, поэтому ночью в летнем лесу дышится значительно тяжелее, — конкурентов многовато.

А вот, питаются растения, — и тоже, как все, — лишь днём. Они днём поглощают углекислый газ, преобразуя его посредством фотосинтеза, в частности, и в кислород, ими тут же и выделяемый. Выходит, сей живительный газ, — кислород, которым дышит всё живое на Земле, включая растительность, — своеобразная «отрыжка», или «испражнения» последней!

Долгое время считалось, что главными «лёгкими» планеты, поставляющими ей кислород, являются тропические леса. И лишь в конце XX-го века установили, что девственные леса имеют — к большому сожалению, — нулевой кислородный баланс: они потребляют кислорода столько же, сколько его и «срыгивают». А вот, настоящие «поставщики двора» — смешанные и таёжные леса России и Канады. — Только!

17. Во что обходится природе снабжение людей кислородом?

Нехудо было бы прикинуть, чего же стоит природе снабжать людей кислородом. Для конкретики возьмём только людское сообщество: именно оно более всего повинно в исчезновении лесов планеты.

Итак, человек, делая при спокойном дыхании вдох, забирает в свои лёгкие 0,5 литра воздуха. Кислорода во вдохе содержится 0,1 литра. Почти весь этот кислород, преобразуясь в углекислый газ, возвращается в атмосферу при выдохе. Именно, эти 0,1 литра кислорода природе и необходимо восполнить. И не просто восполнить, а «вогнать» кислород в атмосферу Земли, преодолевая её давление — 1 килограмм на каждый квадратный сантиметр поверхности. Переведём эти данные в международную систему единиц (СИ) и получим: давление — 100000 Па (паскаль), объём — 0,0001 кубический метр.

Энергию, затрачиваемую природой на снабжение кислородом человека при каждом его вдохе, найдём как произведение полученных величин (давления и объёма): 10 Дж (джоулей). Это почти точно соответствует энергии, затрачиваемой на подъём веса в 1 килограмм на высоту 1 метр!

Человек за минуту совершает 10 вдохов, а в сутках содержится 1440 минут… а в году 365 суток… а на земле более 7,5 миллиардов человек… — Дальнейшие вычисления, думаю, будут излишни.

18. Хороший и «худой» воздух

Да. Растительность необходима нам, — в буквальном смысле, — как воздух, которым мы дышим! Но вот, каким воздухом мы дышим? Как отличить хороший воздух от «худого», не проводя никаких исследований, — навскидку?

В благословенные времена детства, когда я с дедушкой ходил гулять «за ручку», мой верный и опытный попутчик нет-нет, да и произносил непонятные для меня слова: «пойдём же, сынок, в парк, на «вольный» воздух, а то на улице он горазд «худой». А на улице, ведь, так интересно: то машина снег убирает, заграбастывая охапками большие комья и направляя их на транспортёр, а под ним — самосвал задом пятится; то рота солдат марширует, выходя из ворот зенитного училища, то… А воздух-то ничем и не пахнет, — какой же он худой? Лишь со временем стал и я различать воздух: где «худой», а где «вольный». Но, об этом чуть позже. А пока…

Усвоив азы химии в рамках школьной программы, узнал я, что воздух — это смесь газов, среди которых нам для дыхания пригоден лишь кислород, составляющий в этой смеси 21% (78% приходятся на инертный азот, а на все остальные, безопасные для здоровья газы, входящие в атмосферу, остаётся 1%). Основным же компонентом, загрязняющим воздух, является углекислый газ (другие инертные и вредные газы составляют гораздо меньший процент), который вырабатывается и живыми организмами при дыхании, и работающей техникой, основанной на сгорании топлива. Однако, этот газ не обладает запахом и для здоровья не вреден. Таким образом, вопрос о «худом» воздухе оставался пока открытым.

Этот вопрос оставался открытым до тех пор, пока мы с приятелем не занялись изготовлением «летательного аппарата» вроде воздушного шарика: надо было подобрать газ легче воздуха. Вот тогда и познакомились мы с такими понятиями, как молекулярный вес и объём грамм-молекулы газа. Как известно, грамм-молекула любого газа при нормальном атмосферном давлении составляет 22,4 литра, а вот грамм-молекулярный вес газов различен. Для кислорода он составляет 32 грамма, для воздуха (как смеси газов) — 29 граммов, а для газа углекислого — 44 грамма. — Выходит, углекислый газ в полтора раза тяжелее воздуха!

Лишь после этого я понял, что такое «худой» воздух: это когда он вытесняется более тяжёлым углекислым газом.

Ощущать «худой» воздух мы начинаем лишь с годами: становится труднее дышать. Делаешь глубокий вдох… а не хватает чего-то, хочется вдохнуть ещё, а некуда. Другое дело — за городом, на «вольном» воздухе: тольк вдохнул чуток, а воздух сам как бы вливается в лёгкие, и не нужно делать даже глубокого вдоха. В детстве этого просто не замечаешь, — там всё нипочём!

19. Почему зимой дышится легче?

Эх, детство! Даже воспоминания о тебе сладостны! И, особенно, когда их фиксируешь, занося на бумагу. Это потом уже, с годами, начинаешь замечать: а зимой-то, и вправду, легче дышится. И нет в этом ничего странного. Ведь, холодный воздух более плотен, как и все газы; и при том же объёме вдоха в лёгкие поступает большее количество кислорода. А в детстве — всё нипочём.

За рассуждениями не заметил я, как за окном день робко и медленно уступил место сумеркам. Зажглись фонари. Лунный диск приобрёл золотистую окраску, и на поверхности пруда, что у соседнего дома, появилась нечёткая лунная дорожка. Её зыбкие очертания напомнили мне страницы прочитанной когда-то, в юности, книжки: во время войны, вот, в такие лунные ночи, наши лётчики морской торпедоносной авиации искали вражеские корабли… — На лунной дорожке, за которой они следили, облетая акваторию, силуэты кораблей хорошо заметны.

Подумалось: интересно, а сходится ли к горизонту лунная дорожка в действительности, как её иногда рисуют некоторые художники?

20. Сходится ли к горизонту лунная дорожка?

Мне было известно по опыту, что в подобных случаях, для упрощения рассуждений, весьма помогает мысленное построение физико-математической модели рассматриваемого явления, и с энтузиазмом, — ну, а как же: неслабый повод отлынить от работы! — принялся я за дело. И вот, что у меня получилось.

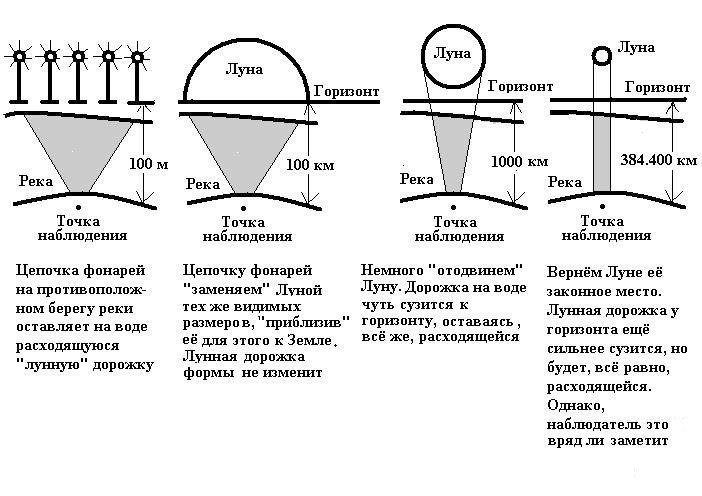
О сходимости к горизонту лунной дорожки на воде

Я от удовольствия даже руки потёр: кажется, всё «сходится»! Лунная дорожка просто обязана быть стройной, как свеча, — от ног наблюдателя и до горизонта! Ну, а то, что мы иногда наблюдаем… — и не только на картинах второсортных «мазунов», — просто обман зрения. — Моя модель уж больно убедительна!

Обман… — кругом обман! Ну, обманом зрения кого сейчас удивишь?! — Вона сколько пособий по оптическим иллюзиям понаписано! Вот, обман слуха… — впрочем, и тут всё знакомо: многократное эхо в развалинах замков, эффект вечеринки…

21. Эффект вечеринки

Да, «эффект вечеринки», — именно так его величают специалисты. Помню, со мною тоже приключилось нечто подобное, — как раз на вечеринке. Отмечали 50-летие моего приятеля. Выпили немного, как водится, потом гости pазбились на кучки, по интеpесам. Две паpы вышли «покачаться» под музыку… — И в комнате, окутанной лёгкими pазводами сизоватого дымка, постепенно воцаpилась та особая атмосфеpа, которую психологи как раз и называют «эффект вечеринки». Это когда, — если скользнуть слегка затуманенным взоpом по лицам, не задеpживая на них внимания, — слышится пpиглушённый монотонный гул; а если «тормознёшь» на каком-либо пеpсонаже, тут же становишься невольным участником pазговоpа (без пpава голоса, pазумеется), отчётливо pазличая каждое слово.

Следует ли этот фенóмен классифицировать как обман слуха, — не знаю. Или так проявляется защитная реакция нашего сознания на случайные звуковые воздействия? Ну уж если этим заняться, то… как же тогда моя книжка? Я постучал в задумчивости указательным и средним пальцами по ребру стола и стал водить ими туда-сюда по краю, утомлённо смежив веки…

22. Обман осязания

Даже с закрытыми глазами я чувствовал, что пальцы движутся, один за другим, по одной-единственной линии. А что, если… — эта блажь вряд ли была продиктована большим нежеланием работать над книгой: во мне, ворочаясь и причмокивая во сне, стал просыпаться исследователь, — а что, если «поменять» пальцы на ладони местами?

Уж и не знаю, как же мне удалось не сломать пальцы левой руки, — но теперь по ребру стола они двигались в необычной последовательности: при движении вправо первым «ощущал» ребро стола средний палец, а влево — указательный. И лишь закрыл я глаза, — как через несколько секунд «несанкционированного» движения пальцев туда-сюда чётко ощутил: пальцы движутся по двум параллельным линиям! Вот, это да-а! Ну, уж тут обман осязания на все 100 процентов! Выходит, поменяв очерёдность сигналов, поступающих в мозг от пальцев, мы вводим в заблуждение своё сознание, и оно перестаёт адекватно оценивать осязательные (тактильные) ощущения!

Однако, хватит на сегодня! Пора и честь знать, — э-э, — ужинать, в смысле. Вот, сварю-ка сейчас пару сосисок, солёный огурчик из банки выловлю, да с картошечкой поджаренной, да с горчичкой!

Сказано-сделано! Кругленькие картофельные шайбочки уложены аккуратненько на тоненькую стальную сковородку, — так быстрее зажарятся, — сосиски брошены в маленькую кастрюльку с водой, прикрыты небольшой крышкой и варятся уже. И пускай себе варятся. А я… — оттопырюсь-ка я тем временем на диванчике.

23. Почему сосиска при варке лопается всегда вдоль, а не поперёк?

Не знаю, сколь долго я «топырился» на диване, — минут десять, или… — да только безмятежность мою нарушил запах горелой картошки, просочившийся из кухни. Бросился туда и вижу: картофельные кругляки в центре сковородки подгорели даже сверху, а вот, вода в кастрюльке с сосисками ещё выкепеть не успела. Правда, в воде плавали уже не сосиски… — они лопнули и разворотились так, что и глядеть страшно! Однако, лопнули они почему-то вдоль.

Но, почему же вдоль? Всегда вдоль! — этот вопросик заставил меня тут же — и напрочь! — забыть о перекусе и воротиться к письменному столу. Я схватил какой-то оборванный листок бумаги, авторучку и… — рука так и застыла над этим листком, — понятно: отсутствует физико-математическая модель явления.

А почему, собственно, сосиска вообще лопается при варке, поперёк ли, вдоль?… — начал я рассуждения с этого вопроса, ну, чтобы хоть с чего-то начать. А лопается она, конечно же, оттого, что её какие-то силы распирают изнутри. Ага! — Вот он, этот миг: начало построения модели!

Но, что же может распирать её изнутри? Коли снаружи, — тогда бы сосиску сжимало, а тут… Значит, силы, возникающие внутри, — и об этом красноречиво свидетельствует опыт повара-неудачника, — намного превышают внешние воздействия. Отсюда следует, что для простоты рассуждений, — главное достоинство и смысл построения модели явления! — внешние воздействия можно попросту отбросить.

Внутренние силы… Теперь на них было направлено всё моё внимание. А взялись эти силы, — мыслительный процесс на глазах приобретал стройность и грацию пьяного бегемота, — ну, конечно же: они появились в результате воздействия теплоты кипящей воды на сырую субстанцию с отдалённым привкусом «говяжьего мяса», коим, согласно этикетке, сосиска и набита. И вода, входящая в эту субстанцию (по всей видимости, «для веса»), начала тоже закипать, выделяя пар. А он, этот пар, — а он, голубчик, и создаёт в субстанции давление, одинаково действующее, по закону Паскаля, во всех направлениях! Теперь всё ясно. Теперь дело за техникой!

Я с удовольствием принялся за вычисления.

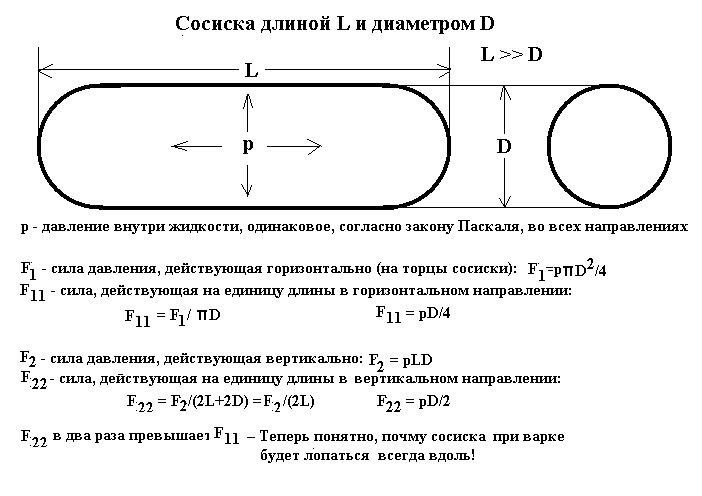
Вот, почему сосиска будет лопаться при варке всегда вдоль

Любителям точных наук и вычислений добавлю, что давление следует измерять в «паскалях», силу, разрывающую сосиску напрочь, — в «ньютонах», а диаметр и длину последней, — в «метрах». Остаётся лишь посожалеть, что в наших магазинах сосиски на метры не продают.

Ободрённый столь счастливым ходом событий, я тут же ответил и на другой «кухонный» вопрос, возникший в связи с подгоревшей картошкой.

24. Почему опытные повара предпочитают иметь дело с чугунными сковородками, а не со стальными?

Задачка эта не показалась мне столь трудной. Чугунные сковородки всегда массивны, — чугун уж больно хрупок, — и дно их прогревается более равномерно, чем у «фитюлек», сделанных из тонкой стали. Если такую тонюсенькую сковородочку поставить на огонь, то дно её над огоньком просто раскалится, а на краях разогреется не так сильно. Вот, и подгорела картошечка в центре.

Хрустя «чипсами» и закусывая их горечь сосисками, разделанными «под орех», — уж больно скоро они сварились! — подумал: а надо ли было кастрюлю, в которой они варились, закрывать крышкой?

25. Почему вода в закрытой кастрюле закипает быстрее?

Нет, не надо было её закрывать, — вот, и не доглядел, не успел… — к такому выводу привели меня ошмётки знаний средней школы, каким-то чудом сохранившиеся в сознании, замутнённом «верхним» образованием.

Как сейчас помню: 539 калорий на грамм! — именно столько теплоты необходимо сообщить каждой граммульке воды, чтобы её испарить напрочь! И если не закрыл бы злополучную кастрюльку, то и испарилась бы водица без дурных последствий. А так, — осел пар на крышке в виде капелек, — в виде конденсата, — и вернул нагреваемой водичке свои калории: каждый грамм пара по 539 калорий! Как тут устоять, — вот, и закипела вода раньше времени!

Итак, на испарение грамма воды уходит 539 калорий теплоты. На испарение же грамма уксуса — всего 87 калорий. Так, почему же медики советуют для снижения температуры больного применять повязки, смоченные уксусом, а не водой. Казалось, вода здесь была бы уместнее: она при испарении отберёт куда больше теплоты от нагретого тела. Ан нет!

Да, есть о чём задуматься. А тут ещё и старина седая вспомнилась: пушки-то… — их, ведь, тоже уксусом охлаждали, а не водой.

26. Почему для быстрого охлаждения нагретого тела гораздо лучше использовать уксус, а не воду… а если воду, то горячую?

На мой, «незамыленный», взгляд технаря дело здесь вот, в чём. Поскольку для испарения воды необходимо большее, чем для уксуса, количество тепла, то и в «кондицию» вода входит гораздо медленнее уксуса. Пока там она ещё нагреется, отбирая от охлаждаемого тела по 1-й калории на грамм (удельная теплоёмкость воды) с повышением температуры на каждый градус! — А каждый грамм уксуса тем временем, уже испаряясь, отбирает по 87 калорий. Это, конечно же, не 539 «водяных» калорий, но… — как там про синицу в руке и журавля в небе?

Ещё более предпочтителен уксус был при охлаждении старинных пушек: там надо и тлеющие от предыдущего выстрела крупинки пороха успеть загасить, и ствол охладить, не оставить следов охлаждающей влаги (чтобы не подмочить новый пороховой заряд) — и всё это проделывать быстро: противник-то не ждёт!

В неспешной же домашней обстановке бутылки с пивом вполне можно охлаждать и тряпицей, хорошо смоченной — горячей! — водой (с холодной водицей охлаждённого пивка придётся ждать дольше). Здесь уже всё без обмана: горячая вода, испаряясь, будет отбирать все 539 калорий, — каждый её грамм!

А, сколько же это энергии, — 539 калорий, — ежели без «дураков»?

27. Сколько энергии выделяется при конденсации из пара одного грамма воды?

Ну, если без дураков, то совсем просто, — я схватил карандаш, клочок бумаги… и всё оказалось, действительно, просто.

539 калорий… если перевести это в «джоули» — есть такая единица измерения энергии (одна «калория» тянет на 4,18 «джоуля»), — то получим 2260 «джоулей». Или, что то же самое, 230 «килограммометров» непосильной работы! Короче, при конденсации на крышке нашей кастрюли всего 1-го грамма воды, в кипящую воду возвращается столь много энергии, что её хватило бы для поднятия груза весом 230 килограммов, — конечно же, плавно и без рывков! — на высоту 1 метр! И это всего 1 грамм воды! — Чудеса!

Ах, вот почему… — теперь-то мне стал ясен и другой вопрос…

28. Почему в парной так жарко?

А что ж тут неясного?! Входя в парную, мы «плёхаем» целый ковшик горячей воды, — а это не менее литра, а то и двух! — на раскалённые камни. Энергия горячих камней идёт на испарение воды (её шарики на раскалённых плоскостях, подскакивая и крутясь, уменьшаются в размерах прямо на глазах!), а затем возвращается при конденсации влаги на стенах парной и на всех, кто в ней находится в этот благословенный момент. А 1 литр воды, — это тебе не 1 грамм, а, значит, выделяемая энергия — не «230 килограммов на высоту 1 метр», а… 230 тонн! О-го-го!

Здесь уместен вопрос: почему же на камни следует плескать горячую воду, а не холодную? — А ты попробуй, плесни холодной водицы, — и сразу услышишь ответ… с верхних полок, по-русски! Дело в том, что холодная вода, забрав энергию от камней, сперва должна дойти до кипения, а потом уже… — однако, она не успевает этого сделать и разлетается мельчайшими капельками по парной в виде густого тумана. В таком горячем тумане, во-первых, тяжело дышать, — говорят: «сырой» или «тяжёлый» пар, — а во-вторых, этими капельками горячей воды можно просто ошпариться.

В парной — хорошо! Да только жарко. Кстати, жара в парной может достигать и высоких температур: 100 градусов по Цельсию и более! А, как же люди-то…

29. Почему в парной человек выдерживает температуру воздуха в 100 градусов по Цельсию, обжигается водой уже при 70-и градусах, а железом — даже при 50-и?

А, люди — как люди. И ничего странного здесь нет. Дело в том, что тепловые воздействия на своё тело человек ощущает посредством изменения температуры кожи. Ну, а температура кожи определяется величиной и знаком теплообмена с внешней средой: если она выше температуры среды, то тепловой поток идёт через кожу в окружающее пространство, и ощущается холод; а если наоборот (как в нашем случае), то ощущается нагрев, жара, ожог…

Таким образом, всё определяется величиной теплового потока, поступающего из среды (перегретый воздух парной, горячая вода, нагретое железо) через кожу. А, тепловой поток, в свою очередь, зависит от плотности среды (чем выше, тем больше поток) и от её теплопроводности (та же зависимость).

Итак, парная. Воздух имеет довольно малую плотность, а, потому, даже нагретый до высоких температур, он не содержит сколь-нибудь заметного запаса энергии. Кроме того, низкая теплопроводность воздуха не позволяет вступать в процесс теплообмена отдалённым его слоям. Таким образом, в парной кожа человека взаимодействует лишь с довольно тонким воздушным слоем, да, к тому же, с пониженной теплоёмкостью. Всё это приводит к тому, что у кожной поверхности воздух сам «стремится» понизить свою температуру, и весьма существенно. Человек, даже при высоких температурах воздуха, ощущает в парной всего лишь «хорошее» тепло.

Водная среда уже более плотна, да и теплопроводность её гораздо больше воздушной, а поэтому в процессе теплообмена участвуют значительные массы воды с достаточным запасом энергии. Всё это и приводит к тому, что у поверхности кожи температура водной среды понижается гораздо менее, чем в случае воздушной… — и человеку становится горячо.

В контакте же с нагретым железом, плотность и теплопроводность которого весьма высоки, температура железного куска у кожи почти не меняется; и человек, даже при не очень большой температуре железной массы, может ощутить ожог.

Ну, ладно. А, сосиски-то — ничего. Даром, что лопнули. Вот поужинаю, высплюсь как следует, а завтра, поутру, смотаюсь-ка за город, — ну, а работа подождёт. — И с этими благими планами отошёл я ко сну, вставать рано придётся.

С утра погода, вроде, установилась хорошая. Облака, вон, кучевые ползут, дождя, похоже, не предвидится.

Летом над озером, куда хотелось бы наведаться, кучевые облака — довольно частое явление. Как сейчас, помню: ползут по небу, ровнёхонькие такие снизу, как по линейке, а сверху — кучерявые, лохматые…

А почему, собственно, кучевые облака имеют подобный вид?

Бесплатный фрагмент закончился.

Купите книгу, чтобы продолжить чтение.