Бесплатный фрагмент - Пирамида чисел Фибоначчи — Кучина

Пирамида чисел Фибоначчи — Кучина, часть 1

Итак, уважаемый читатель, перед Вами книга о Пирамиде чисел Фибоначчи — Кучина. Такое громкое название связано с тем, что в далеком 2008 году мне совершенно случайно, более того 13 июля, более того в день рождения моей супруги, удалось найти удивительное математическое построение алгебраического ряда нового типа. Более года я искал своих математических предшественников и, представьте, не нашел.

Читатель вправе спросить — а зачем все это? И я дам ему ответы! Но придется немного потерпеть, и собственно построить Пирамиду чисел Фибоначчи — Кучина. Делать мы будем это поэтапно. Метод построения не сложен, и «въехать» в этот метод нам помогут авторские картинки.

Важно подчеркнуть, что мы нашу пирамиду чисел будем строить не с низа вверх, а сверху вниз, но привыкнуть к такому методу построения несложно.

Небольшой совет: читать научный комикс «Пирамида чисел Фибоначчи — Кучина» лучше всего с карандашом в руках, чтобы проверить все построения, которые будет выполнять автор — это поможет читателю понять все идеи автора. А в сложных случаях поможет простой калькулятор.

Пирамида чисел Фибоначчи — Кучина, часть 2

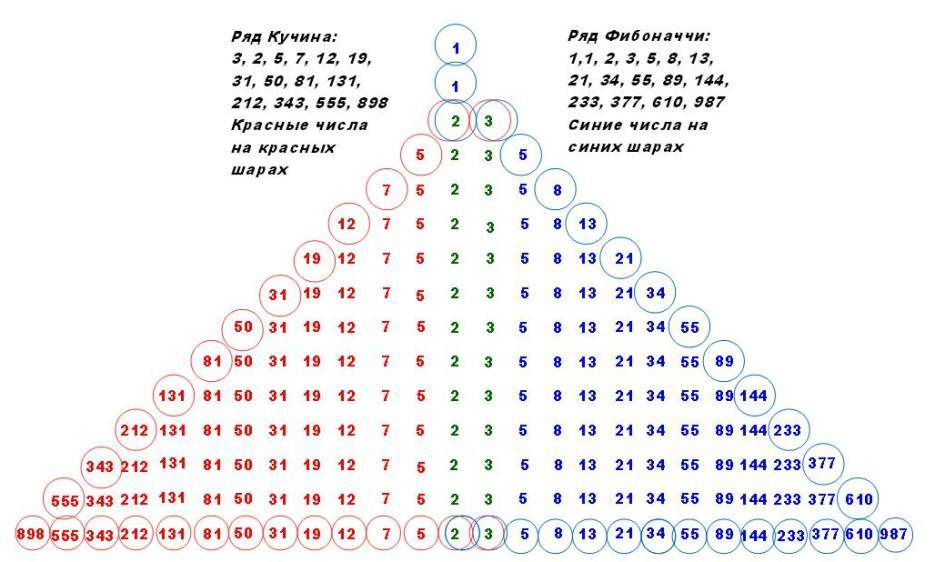
Внимательно смотрим на иллюстрацию!

Что такое алгебраический ряд?

Это последовательность чисел, построенная по определенному закону. У ряда всегда есть первое число, второе число, и т. д.

Ряд Фибоначчи начинается с первого числа «1» — оно в самом верхнем квадратике картинки. ВСЕ ЧИСЛА ФИБОНАЧЧИ ГОЛУБЫЕ. Следующее число Фибоначчи — ниже первого, тоже «1». Третье число Фибоначчи «2» образуется по формуле 2=1+1 — это сумма первого и второго числа.

Число «2» — ЗЕЛЕНОЕ — эти числа относятся и к ряду Фибоначчи и к ряду Кучина.

Пока все числа у нас шли сверху вниз.

Четвертое число Фибоначчи это сумма второго и третьего чисел, т.е. 3=1+2.

Разместим это число на первой ступени пирамиды Фибоначчи — Кучина слева от числа «2». Число «3» тоже ЗЕЛЕНОЕ, оно входит в оба ряда.

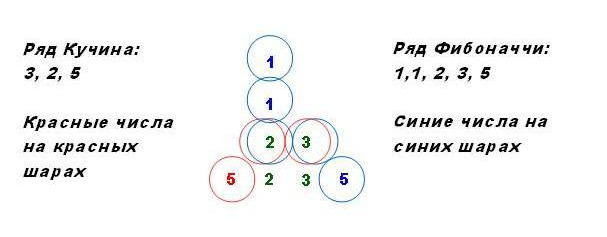
А теперь главное:

ЧИСЛА ФИБОНАЧЧИ МЫ БУДЕМ ПОЛУЧАТЬ СУММИРОВАНИЕМ ДВУХ ПРЕДЫДУЩИХ СЛЕВА НАПРАВО (!!!) И ПОМЕЩАТЬ НА ПРАВЫЙ СКЛОН ПИРАМИДЫ — ВСЕ ОНИ ГОЛУБЫЕ.

ЧИСЛА КУЧИНА МЫ БУДЕМ ПОЛУЧАТЬ СУММИРОВАНИЕ ДВУХ ПРЕДЫДУЩИХ СПРАВА НАЛЕВО (!!!) И ПОМЕЩАТЬ НА ЛЕВЫЙ СКЛОН ПИРАМИДЫ — ВСЕ ОНИ КРАСНЫЕ.

Найдем новые числа.

Четвертое число Фибоначчи, это сумма двух предыдущих 2+3=5. Поместим эту голубую пятерку СПРАВА от тройки.

Третье число Кучина, это сумма двух предыдущих, но суммирование идет СПРАВА — НАЛЕВО (!!!) 3+2=5. Поместим эту красную пятерку СЛЕВА от зеленой двойки.

Перед нами две верхние ступени «Пирамиды чисел Фибоначчи — Кучина».

Вершина: 2,3

Вторая ступень: 5,2,3,5.

Продолжим это строительство в следующей статье.

Тех, кто дочитал это сообщение, я прошу взять карандаш или ручку и повторить на бумаге наши построения. Уверяю вас — польза от этого будет!

И продолжать эту простую работу при последующем чтении научного комикса.

Пирамида чисел Фибоначчи — Кучина, часть 3

Все необходимые пояснения и построение первых двух ступеней «Пирамиды чисел Фибоначчи — Кучина» даны в части 2.

Начинаем строить третью ступень пирамиды.

Находим число из ряда Кучина как 2+5=7 и пишем его слева.

Находим число из ряда Фибоначчи как 3+5=8 и пишем его справа.

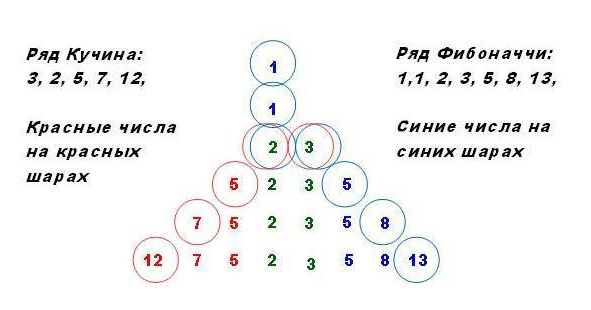
Строим четвертую ступень пирамиды.

Находим число из ряда Кучина как 5+7=12 и пишем его слева.

Находим число из ряда Фибоначчи как 5+8=13 и пишем его справа.

У нас уже получилась пирамида из четырех ступеней.

На ее левом склоне в направлении вниз-налево стоят числа из ряда Кучина: 2,5,7,12

На ее правом склоне в направлении вниз-направо стоят числа из ряда Фибоначчи:

3,5,8,13.

Вершину образуют общие числа (зеленые) 2,3

На самом верху два начальных числа из ряда Фибоначчи 1,1.

Продолжим построение в части 4.

Пирамида чисел Фибоначчи — Кучина, часть 4

Понемногу приближаемся к цели построения — когда последнее число ряда Кучина приблизиться по значению к 1000.

Все необходимые пояснения и построение первых 4-х ступеней «Пирамиды чисел Фибоначчи — Кучина» даны в частях 2, 3.

Начинаем строить пятую ступень пирамиды.

Находим число из ряда Кучина как 7+12=19 и пишем его слева.

Находим число из ряда Фибоначчи как 8+13=21 и пишем его справа.

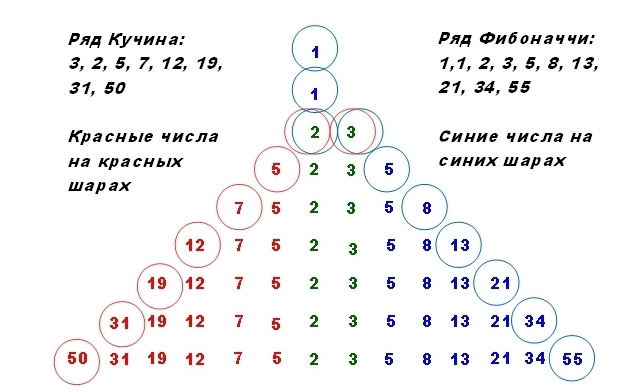
Строим шестую ступень пирамиды.

Находим число из ряда Кучина как 12+19=31 и пишем его слева.

Находим число из ряда Фибоначчи как 13+21=34 и пишем его справа.

Строим седьмую ступень пирамиды.

Находим число из ряда Кучина как 19+31=50 и пишем его слева.

Находим число из ряда Фибоначчи как 21+34=55 и пишем его справа.

У нас уже получилась пирамида из семи ступеней.

На ее левом склоне в направлении вниз-налево стоят числа из ряда Кучина: 2,5,7,12, 19, 31, 50.

На ее правом склоне в направлении вниз-направо стоят числа из ряда Фибоначчи:

3,5,8,13, 21, 34, 55.

Вершину образуют общие числа (зеленые) 2,3

На самом верху два начальных числа из ряда Фибоначчи 1,1.

Продолжим построение в части 5.

Пирамида чисел Фибоначчи — Кучина, часть 5

Понемногу приближаемся к цели построения — когда последнее число ряда Кучина приблизиться по значению к 1000.

Все необходимые пояснения и построение первых 7-ми ступеней «Пирамиды чисел Фибоначчи — Кучина» даны в частях 2, 3, 4.

Начинаем строить восьмую ступень пирамиды.

Находим число из ряда Кучина как 31+50=81 и пишем его слева.

Находим число из ряда Фибоначчи как 34+55=89 и пишем его справа.

Строим девятую ступень пирамиды.

Находим число из ряда Кучина как 50+81=131 и пишем его слева.

Находим число из ряда Фибоначчи как 55+89=144 и пишем его справа.

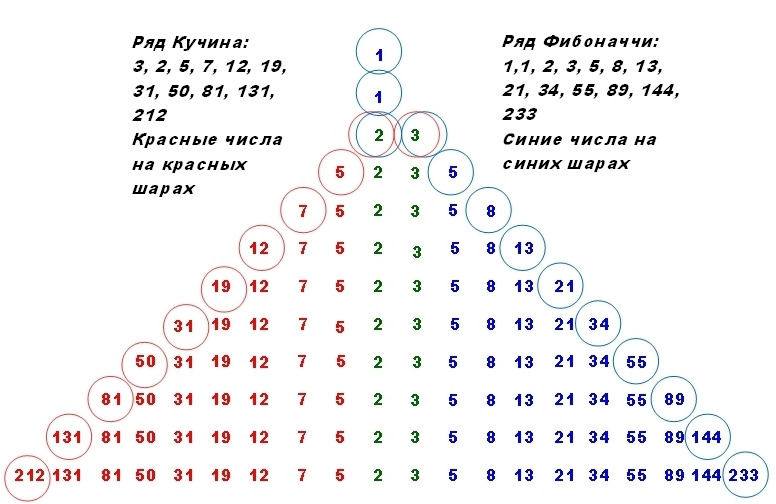
Строим десятую ступень пирамиды.

Находим число из ряда Кучина как 81+131=212 и пишем его слева.

Находим число из ряда Фибоначчи как 89+144=233 и пишем его справа.

У нас уже получилась пирамида из десяти ступеней.

На ее левом склоне в направлении вниз-налево стоят числа из ряда Кучина: 2,5,7,12, 19, 31, 50, 81, 131, 212.

На ее правом склоне в направлении вниз-направо стоят числа из ряда Фибоначчи:

3,5,8,13, 21, 34, 55, 89, 144, 233.

Вершину образуют общие числа (зеленые) 2,3

На самом верху два начальных числа из ряда Фибоначчи 1,1.

Продолжим построение в части 6 — завершающей.

Пирамида чисел Фибоначчи — Кучина часть 6

Внимание, сейчас мы достроим «Пирамиду чисел Фибоначчи — Кучина».

Все необходимые пояснения и построение первых 10-ти ступеней «Пирамиды чисел Фибоначчи — Кучина» даны в частях 2, 3, 4, 5.

Начинаем строить одиннадцатую ступень пирамиды.

Находим число из ряда Кучина как 131+212=343 и пишем его слева.

Находим число из ряда Фибоначчи как 144+233=377 и пишем его справа.

Строим двенадцатую ступень пирамиды.

Находим число из ряда Кучина как 212+343=555 и пишем его слева.

Находим число из ряда Фибоначчи как 233+347=610 и пишем его справа.

Строим тринадцатую ступень пирамиды.

Находим число из ряда Кучина как 343+555=898 и пишем его слева.

Находим число из ряда Фибоначчи как 377+610=987 и пишем его справа.

У нас уже получилась пирамида из тринадцати ступеней.

На ее левом склоне в направлении вниз-налево стоят числа из ряда Кучина: 2,5,7,12, 19, 31, 50, 81, 131, 212, 343, 555, 898.

На ее правом склоне в направлении вниз-направо стоят числа из ряда Фибоначчи:

3,5,8,13, 21, 34, 55, 89, 144, 233, 377, 610, 987.

Вершину образуют общие числа (зеленые) 2,3

На самом верху два начальных числа из ряда Фибоначчи 1,1.

Итак, пирамида построена. Она обладает одним очень простым, но не очевидным чудесным математическим свойством, которое я объясню в следующей главе.

В следующих статьях (главах) мы обсудим калибрующую роль чисел ряда Кучина и связанных с ними чисел Фибоначчи в окружающем нас мире.

Пирамида чисел Фибоначчи-Кучина, лестница к Солнцу

Мы завершаем строительство Пирамиды чисел Фибоначчи — Кучина.

Но какая пирамида без лестницы? Вот ее мы и построим.

Перед вами рисунок пирамиды чисел Фибоначчи — Кучина, на котором желтыми стрелками обозначены ступени ДЕСЯТИЧНОЙ ЛЕСТНИЦЫ. Да, автор не оговорился — и это существенное открытие в области науки о числах.

Мы строили левый и правый склоны пирамиды используя очень простые формулы сложения двух чисел для получения третьего (см. части 2—6). На левый склон пирамиды мы ставили числа из ряда Кучина, а на правый числа из ряда Фибоначчи.

И вот, числовая пирамида была достроена. Вертикальная формула построения пирамиды была понятна, но, оказывается, числа в пирамиде из ряда Кучина и ряда Фибоначчи СВЯЗАНЫ ГОРИЗОНТАЛЬНО ПО ДЕСЯТИЧНОЙ ПРОПОРЦИИ!!!

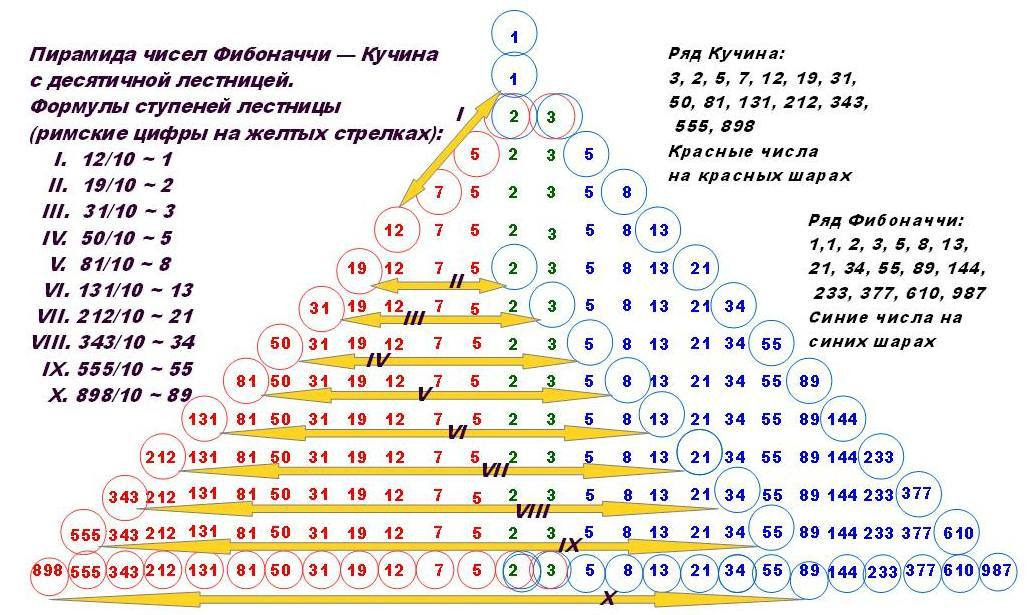
Формулы связи указаны на чертеже пирамиды. В данном случае число из ряда Кучина нужно разделить на 10 — это основание общепринятой десятичной системы — и округлить до целого.

Например, число из ряда Кучина «81» деленное на 10 дает «8,1» — округляем — «8». А это число из ряда Фибоначчи 8, которое стоит НА ЭТОЙ ЖЕ СТУПЕНИ ПИРАМИДЫ, ТОЛЬКО НА 10-й ПОЗИЦИИ СПРАВА. И так далее, все очень просто и весьма удивительно.

Так на Пирамиде чисел Фибоначчи — Кучина образовалась лестница из 10-ти ступеней, своеобразная «лестница к Солнцу», по которой можно подняться от подошвы пирамиды, от чисел «898 — 89», к ее вершине, числу «1». До числа «19» мы поднимемся без проблем, а от числа «12» к «1» залезем по желтой «альпинистской» веревке.

Представим себе, что мы виртуально стоим на вершине Пирамиде чисел Фибоначчи — Кучина и смотрим вокруг.

И, оказывается, что в окружающем нас мире числа из ряда Кучина, связанные удивительным десятичным соотношением с числами Фибоначчи, играют очень большую роль, они присутствуют в законах химии, физики, в природных явлениях, в скорости звука, в скорости света, в физических постоянных, в медицине, в геометрии.

Не пытаясь объять необъятное, расскажем о некоторых примерах «жизни» чисел из Пирамиды чисел Фибоначчи — Кучина в окружающем нас мире.

Пирамида чисел Фибоначчи — Кучина. Золотое сечение

В последней статье — «Пирамида чисел Фибоначчи — Кучина. Лестница к солнцу» — автор показал, что пирамида чисел действительно существует, и обладает неожиданным десятичным свойством. Это свойство состоит в ДЕСЯТИЧНОЙ связи чисел ряда Кучина и чисел ряда Фибоначчи, что позволяет построить на пирамиде десятичные ступени.

Продолжим наши поиски и поговорим о ЗОЛОТОМ СЕЧЕНИИ. Этот термин имеет древнюю историю, в ней переплелись и математика и мистика и всякие оккультные идеи.

Автора в данном случае интересуют только факты. Поэтому обратимся к Большой Советской Энциклопедии, где прочитаем:

«ЗОЛОТОЕ СЕЧЕНИЕ, гармоническое деление, деление в крайнем и среднем отношении, деление отрезка АВ на две части т.о., что большая его часть АС является средней пропорциональной между всем отрезком АВ и меньшей его частью СВ ….

Алгебраич. нахождение 3.с. отрезка АВ = а сводится к решению уравнения… откуда х ~ 0,62.

Отношение х к а может быть также выражено приближённо дробями 2/3, 3/5, 5/8,

8/13, 13/21 и т. д., где 2, 3, 5, 8, 13, 21 и т. д.- Фибоначчи числа.»

Принято в честь древнегреческого архитектора Фидия обозначать число равное 1/х, где х — корень решения уравнения, о котором идет речь в энциклопедии, символом Ф.

С точностью до шести знаков после запятой Ф = 1,618034.

Множество материалов, написанных в основном в 19-м и начале 20-го века содержать сведения о РАЦИОНАЛЬНОМ ПРИБЛИЖЕНИИ к ЗОЛОТОМУ СЕЧЕНИЮ с помощью чисел Фибоначчи.

Самый доступный способ в этом убедиться — обратиться к Википедии по ссылке — https://ru.wikipedia.org/wiki/Золотое_сечение.

Автор статьи о ЗОЛОТОМ СЕЧЕНИИ в Википедии пишет:

«Рациональные приближения — 3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; … и. т. д. F {n+1} /F {n}, где F {n} — числа Фибоначчи (перечислено в порядке увеличения точности).»

А теперь пора обратиться к иллюстрации к нашей статье.