The authors, Boris Zlotin, the developer of the theoretical foundations of the PANN and software products based on it, and Vladimir Matsenko, an implementer of these products and participant in the creation and testing of the theory, express their gratitude to those who helped in this work and made a substantial creative contribution:

• Dmitry Pescianschi, the founder of the general idea of a new approach to neural network design.

• Vladimir Proseanic, Anatol Guin, Sergey Faer, Oleg Gafurov, and Alla Zusman, who actively supported the development of PANN with their experience and knowledge in the Theory of Inventive Problem Solving (TRIZ) and their talents.

• Ivan Ivanovich Negreshny — for his constructive criticism, which helped the authors recognize and correct their shortcomings.

Part 1. A New Kind of Neural Network: Progress Artificial Neural Network (PANN)

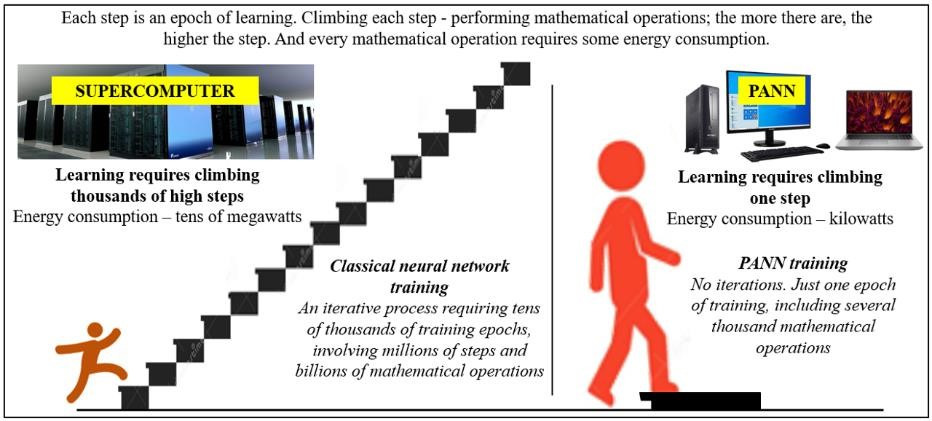
1. Introduction to the Problem

Where did neural networks come from, and why are we unsatisfied with them?

The development of artificial neural networks began with the work of Turing, McCulloch, Pitts, and

Hebb. Based on their ideas, in 1958, Frank Rosenblatt created the first artificial neural network,

“Perceptron,” capable of recognizing and classifying different objects based on recognition after appropriate training. Unfortunately, the very concept of the perceptron was fraught with a critical flaw, based on then-prevailing Dale’s biological doctrine: “…A neuron uses one and only one neurotransmitter for all synapses.” This doctrine was transferred to all artificial neural networks through a rule: “…One artificial synapse uses one and only one synaptic weight.” This rule may be called the Rosenblatt Doctrine.

In the 1970s, Dale’s doctrine was rejected by biological science. Unfortunately, Rosenblatt’s doctrine remains unchanged for all neural networks (recurrent, resonant, deep, convolutional, LSTM, generative, forward, and backward error propagation networks). This doctrine makes it possible to train networks using an iterative approach known as the gradient descent method, which requires enormous computation. And it is precisely this doctrine that is “to blame” for the inability to construct an adequate working theory of neural networks. Also, these networks are characterized by opacity and incomprehensibility, relatively low training speed, difficulty in completing training, and many other innate problems. For more information on the issues of classical neural networks, see Appendix 1.

Therefore, the development of such networks is mainly by trial and error. This leads to complexity and low reliability, the need for costly equipment, conducting complex power-hungry calculations, and expensive manual labor to provide training.

The critical “Rosenblatt error” was discovered by researchers (TRIZ specialists) of the deep tech company Progress, Inc. They also found a solution to eliminate this error. Thus, it became possible to create a fundamentally new type of neural network called PANN (Progress Artificial Neural Network). PANN networks and their operations are transparent, predictable, and thousands of times less costly, providing a better solution to many intelligent tasks. Eighteen patents in many countries worldwide protect PANN’s designs and operations. Several new software versions have already been created and tested based on these concepts.

2. Scientific and technical foundations of the PANN network

In this chapter, we will describe the main design features and the theoretical basics of the PANN network.

PANN differs from classical neural networks in that it has a unique design for the main element: the so-called formal neuron. A new formal neuron allows for a different way of training. As a result:

1. The network operation has become completely transparent. Establishing a simple and straightforward theory that predicts the results of actions has become possible.

2. PANN can be implemented on low-cost hardware. Its training and operation costs are much lower than those of classical neural networks.

3. PANN trains many times faster than classical neural networks.

4. PANN can be trained to additional (new) data anytime.

5. PANN does not have the harmful effect of “overfitting.”

2.1. A NEW DESIGN OF THE FORMAL NEURON

Classical neural networks are built of typical “bricks” — formal neurons of simple design, described by McCulloch and Pitts and implemented by Rosenblatt. The main problem with neural networks is the poor design of this formal neuron.

A formal Rosenblatt neuron has one synaptic weight. The PANN’s unique feature is a formal Progress neuron with two or more synaptic weights at each synapse.

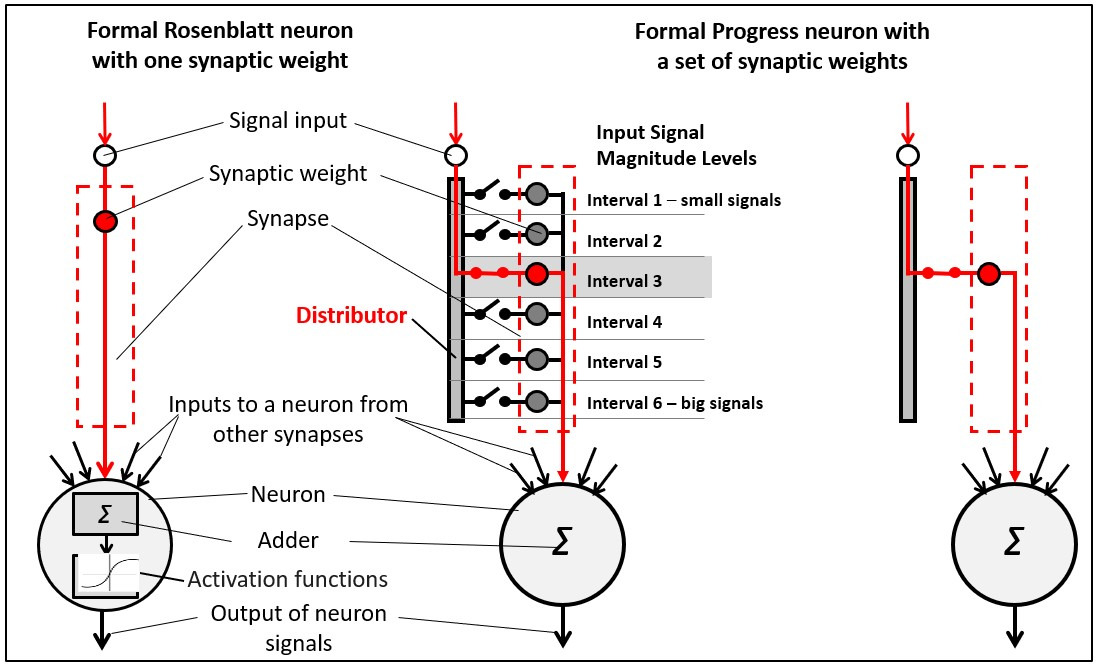
In the Progress neuron, as in the Rosenblatt neuron, input signals travel to the adder through a single synaptic weight. However, in the Progress neuron, the distributor selects the weight based on the input signal size.

The main characteristics that describe the Progress neuron are:

• The Progress neuron operates with images presented as numerical (digital) sequences. These can be pictures, films, texts, sound recordings, tables, charts, etc.

• Each Progress neuron is connected to all network inputs. The number of inputs equals the number of digits in the digital sequence (image). For images in raster graphics, this is the number of pixels. For example, at a resolution of 16 × 16, the number of inputs I = 256; at a resolution of 32 × 32, the number of inputs I = 1024.

• The number of synaptic weights of the Progress neuron is at least two. When working with black-and-white graphics and simple tables, it is possible to use only two weights (“0” and “1”). When working with color pictures, you can use any graphical representation, for example, palettes of 2, 4, 8, 16, 256, and so on. It should be noted that for the effective recognition of different types of images, there are optimal palettes, which are easy to determine by simple testing. At the same time, an unexpected property of PANN appears: the optimal number of colors for recognition is usually small; in experiments, this number was generally between 6 and 10.

• The number of inputs is the number of members of the digital sequence in question; for images in raster graphics, the number of pixels must be the same for all images under consideration. For example, at a resolution of 16 × 16, the number of inputs is I = 256; at a resolution of 32 × 32, the number of inputs is I = 1024. You can use any aspect ratio of rectangular images when working with images. It should be noted that for the effective recognition of different types of images, there are their own optimal resolutions, which are easy to determine with simple testing. At the same time, an unexpected property of PANN manifests itself — the optimal number of pixels for recognition is usually small; for example, for the recognition of various kinds of portraits, the best resolution can be 32 × 32.

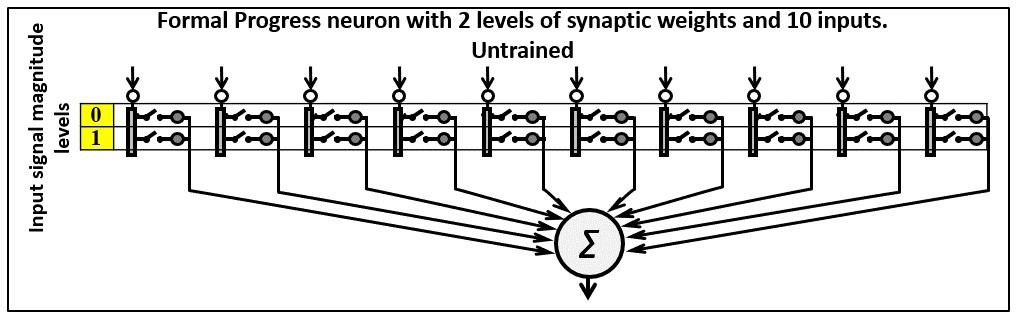
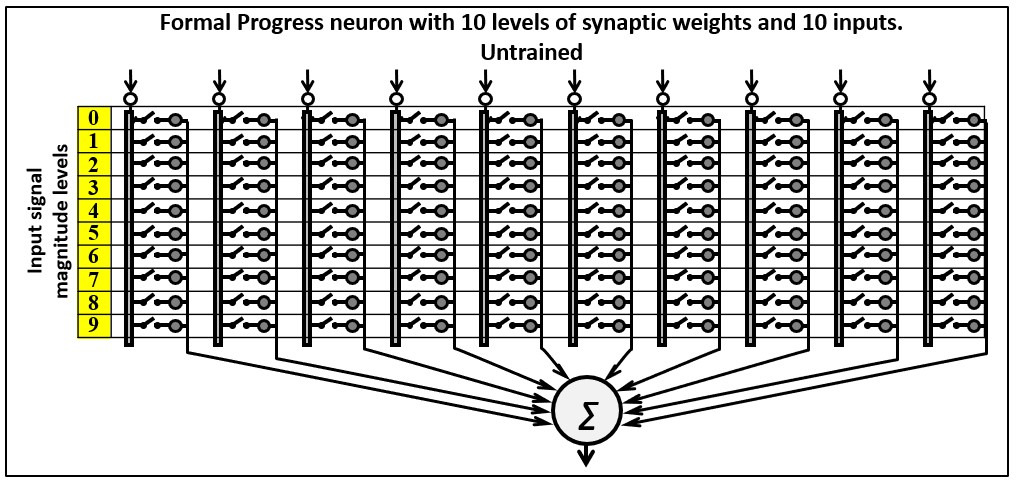
Fig. 2. Single-neuron two-level PANN network

Fig. 3. Single-neuron multi-level PANN network

2.2. PROGRESS NEURON TRAINING

Training a PANN network is much easier than training any classical network.

The difficulties of training classical neural networks are related to the fact that when training several different ones, some images affect the synaptic weights of other images and introduce distortions in training into each other. Therefore, one must select weights so their set corresponds to all images simultaneously. To do this, they use the gradient descent method, which requires many iterative calculations.

A fundamentally different approach was developed to train the PANN network: “One neuron, one image,” in which each neuron trains its own image. At the same time, there are no mutual influences between different neurons, and training becomes fast and accurate.

The training of the Progress neuron to a specific image boils down to the distributor determining the signal level (in the simplest case, its amplitude or RGB value) and closing the switch corresponding to the range of weights in which this value falls.

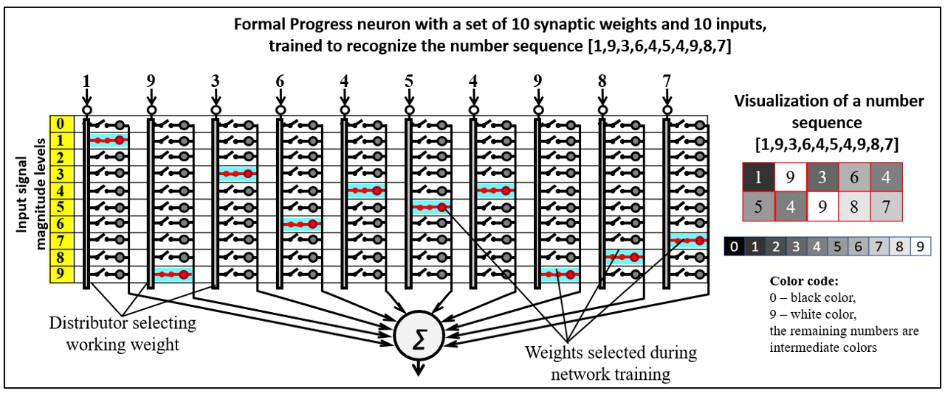
Fig. 4. Trained single-neuron multi-level PANN network

The above training procedure of the Progress neuron gives rise to several remarkable properties of the PANN network:

1. Training does not require computational operations and is very fast.

2. One neuron’s set of synaptic weights is independent of other neurons. Therefore, the network’s neurons can be trained individually or in groups, and then the trained neurons or groups of neurons can be combined into a network.

3. The network can retrain — i.e., it is possible to change, add, and remove the necessary neurons at any time without affecting the neurons unaffected by these changes.

4. A trained image neuron can be easily visualized using simple color codes linking the included weights’ levels to the pixels’ brightness or color.

2.3. THE CURIOUS PARADOX OF PANN

At first glance, the PANN network looks structurally more complex than classical Artificial Neural Networks. But in reality, PANN is simpler.

The PANN network is simpler because:

1. The Rosenblatt neuron has an activation factor; in other words, the result is processed using a nonlinear logistic (sigmoid) function, an S-curve, etc. This procedure is indispensable, but it complicates the Rosenblatt neuron and makes it nonlinear, which leads to substantial training problems. In contrast, the Progress neuron is strictly linear and does not cause any issues.

2. The Progress neuron has an additional element called a distributor, which is a simple logic device: a demultiplexer. It switches the signal from one input to one of several outputs. In the Rosenblatt neuron, weights are multi-bit memory cells that can store numbers over a wide range, while in PANN, the most superficial cells (triggers) can be used, which can store only the numbers 1 and 0.

3. Unlike classic networks, PANN does not require huge memory and processing power of a computer, so cheap computers can be used, and much less electricity is required.

4. PANN allows you to solve complex problems on a single-layer network.

5. PANN requires tens or even hundreds of times fewer images in the training set.

Thus, it is possible to create full-fledged products based on PANN, using computer equipment that is not very expensive and economical in terms of energy consumption.

Fig. 5. Long and expensive training vs. fast and cheap

2.4. THE MATHEMATICAL BASIS OF RECOGNITION

ON THE PROGRESS NEURON

The linearity of the Progress neuron leads to the fact that the network built on these neurons is also linear. This fact ensures its complete transparency, the simplicity of the theory describing it, and the mathematics applied.

In 1965, Lotfi Zadeh introduced the concept of “fuzzy sets” and the idea of “fuzzy logic.” To some extent, this served as a clue for our work in developing PANN’s mathematical basis and logic. Mathematical operations in PANN aim to compare inexactly matching images and estimate the degree of their divergence in the form of similarity coefficients.

2.4.1. Definitions

In 2009, an exciting discovery was made called the “Marilyn Monroe neuron” or, in other sources, “grandmother’s neuron.” In the human mind, knowledge on specific topics is “divided” into individual neurons and neuron groups, which are connected by associative connections so that excitation can be transmitted from one neuron to another. This knowledge and the accepted paradigm of “one neuron, one image” made building the PANN recognition system possible.

Let’s introduce the “neuron-image” concept — a neuron trained for a specific image. In PANN, each neuron-image is a realized functional dependency (function) Y = f (X), wherein:

X is a numerical array (vector) with the following properties:

for X = A, f (A) = N

for X ≠ A, f (A) <N

A is a given value.

N is the dimension of vector X, the number of digits in this vector.

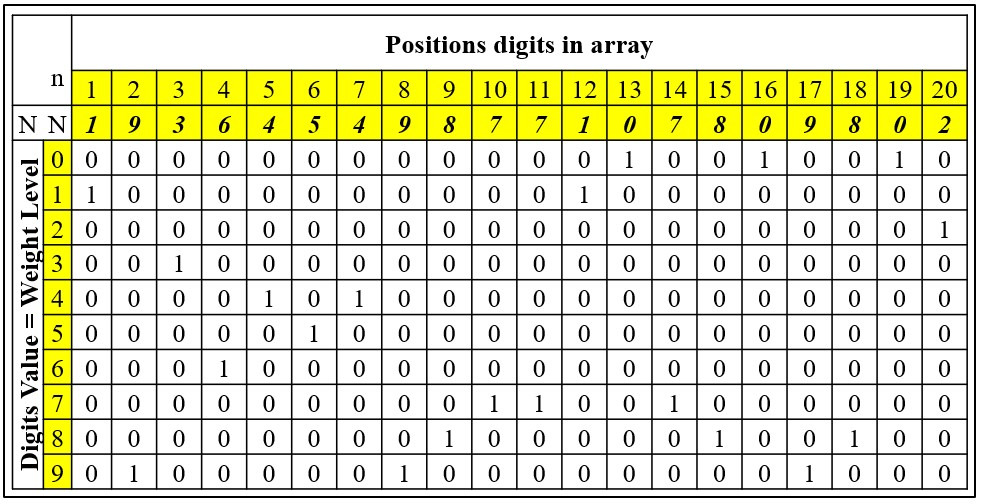
This format, called the Binary Comparison Format (BCF), is a rectangular binary digital matrix in which:

• The number of columns is equal to the length N (the number of digits) of the array.

• The number of rows equals the number of weight levels K selected for the network.

• Each significant digit is denoted by one (1) in the corresponding line, and the absence of a digit is denoted by zero (0).

• Each string corresponds to some significant digit of the numeric array to be written, i.e., in a string marked as “zero,” the digit “1” corresponds to the digit “0” in the original array, and in a string marked as “ninth,” the digit “1” corresponds to the digit 9 in the array.

• In each column of the matrix, one unit corresponds to the value of this figure, and all other values in this column are equal to 0.

• The sum of all units in the array matrix is equal to the length N of the array; for example, for an array of 20 digits, it is 20.

• The total number of zeros and ones in the matrix of each array is equal to the product of the length N of this array and the value of the base of the number system used.

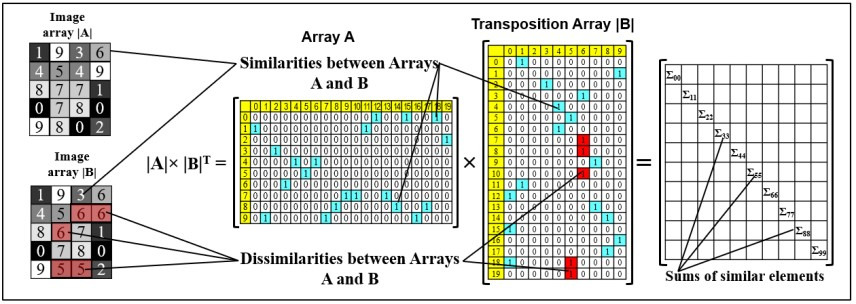
Example: BCF notation of an array of 20 decimal digits [1, 9, 3, 6, 4, 5, 4, 9, 8, 7, 7, 1, 0, 7, 8, 0, 9, 8, 0,2].

Fig. 6. BCF image as a sparse binary matrix

A feature of the PANN network is that the image training of neurons typical of neural networks can be replaced by reformatting files that carry numerical dependencies to the BCF format or simply loading files in this format to the network.

Type X arrays in BCF format are denoted as matrices |X|.

2.4.2. Comparing Numeric Arrays

Comparing objects or determining similarities and differences

Determining the similarity of particular objects by comparing them plays an enormous role in thinking, making it possible to identify analogies and differences between different objects — beings, objects, processes, ideas, etc. In various branches of science, primarily in the Theory of Similarity, dimensionless similarity coefficients or similarity criteria (Similarity Coefficient or CoS) are used, sometimes called the “measure of similarity,” the “measure of association,” and so on.

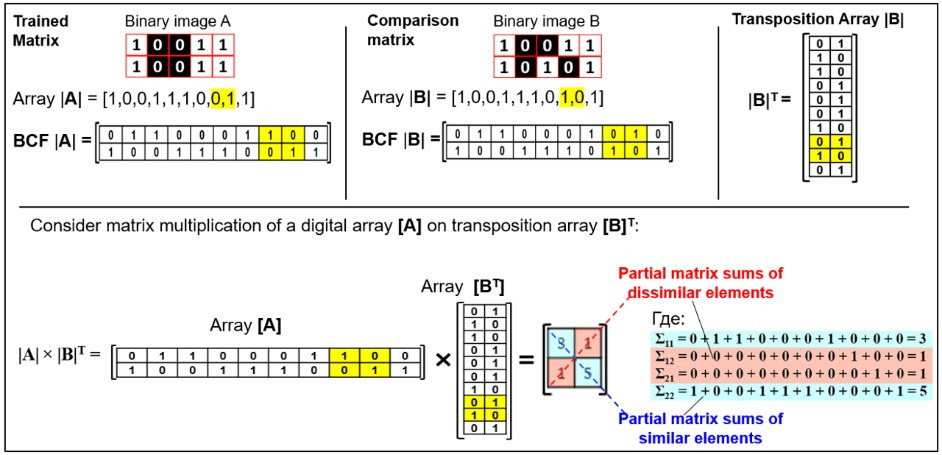
Comparison functions in PANN are implemented through mathematical operations on matrices of numeric arrays. Let’s consider the most straightforward comparison algorithm, which uses the vector product of image neuron matrices.

Two arrays are given for comparison in the form of matrices |X1| and |X2|.

|X1| × |X2|T is the vector product of the matrix |X1| on a transposed matrix |X2|. Moreover, the value of this product is proportional to the number of units in |X1| and |X2|.

|X1| × |X2|T = N only if |X1| = |X2|;

|X1| × |X2|T <N if |X1| ≠ |X2|;

|X1| × |X2|T = 0 if none of the pixels of these matrices match.

Consider the relationship:

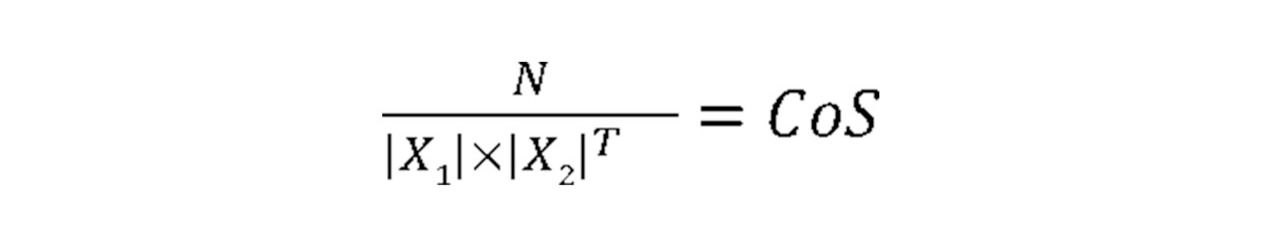
Here, the CoS (Similarity Coefficient) between the numerical vectors X1 and X2 determines the degree of closeness of these vectors and the images described by these vectors.

Examples:

Fig. 7. Multiplying matrices to compare numerical arrays

Fig. 8. Comparison of decimal numerical arrays |A| and |B|

Classical neural networks only determine which class a recognizable object is most similar to. At the same time, they cannot specify how similar it is. Because of this, recognition is sometimes unstable — there are well-known examples where a change in a pixel in an image was enough to change its recognition. Thus, recognition in classical networks is highly dependent on random noise.

In PANN, the situation is different — the similarity coefficient value very clearly shows how significant the difference between the images is. A similarity difference of one hundredth in the format of 32 × 32 pixels corresponds to a change of about 10 pixels. And this is already enough to distinguish the images from each other confidently. The one-tenth difference indicates a profound difference and high recognition stability — low dependence of recognition on noise.

In contrast to classical neural networks, PANN networks allow you to improve the quality of recognition dramatically by:

• Statistical processing of recognition by classes and by images.

• Combining class-based recognition and image-based recognition. Moreover, combined recognition by classes and images allows us to solve one of the most unpleasant problems that limit the use of neural networks in medicine and many other applications — the problem of transparency and explainability of the network results. We will discuss this in l in the “4.6. Recognition on the PANN Network” section.

2.4.3. Assessment of the validity and accuracy of recognition

The validity and accuracy of image recognition by neural networks are essential for their use.

The accuracy and reliability of recognition of a classical neural network are determined by testing several dozens, hundreds, or thousands of images and counting the number of correct and incorrect recognitions. This test is very controversial. Due to the opacity of classical networks, recognition is highly dependent on random training features:

• Sometimes, training outcomes are poorly reproduced; the same network trained on the same images will recognize better in some cases than worse in others.

• There are no ways to assess each image’s accuracy and recognition reliability adequately.

• Impact of test image selection. Sometimes, they are selected specifically to ensure the desired result.

Recognition by PANN networks is evaluated by the numerical similarity coefficient of the image under consideration:

1. With any set of individual images loaded to the network.

2. With all classes that this network is trained in.

At the same time, both classes and individual images are ranked according to the degree of similarity, which allows for an accurate assessment of the magnitude of the differences between all the compared classes and, thereby, assessment of the accuracy and reliability of recognition.

Of course, formally correct recognition (from the point of view of a machine) is possible, but it is not satisfactory. People often recognize others not by their main features but by secondary ones. For example, we can evaluate similarity not by facial features but depending on clothes. It happens that when recognizing human faces, the features of the lighting are more significant than the facial features.

Problems of this kind can be solved in PANN in several ways, in particular:

1. Equalization of illumination by known graphical or mathematical means.

2. Introduction of a system for assessing the weight of features and filtering some features.

3. Create a set of intersecting classes, as shown below.

4. Create a “recognition committee” — a logical expert system that concludes based on the sum of recognitions for different classes and images. Thus, it reproduces what a person does by looking closely at the object.

2.4.4. Indexing Number Sequences in BCF

Indexing for quick retrieval of information.

Today, search indexing is widely used in computer science. Index files make it easier to find information and are ten times smaller than the original files. However, indexing is more difficult for different types of files (for example, graphics), and search does not always work adequately. PANN allows for a more organized and standardized approach to indexing and searching.

Using Progress Binary Comparison Format (BCF), you can build standard and universal search indices, i.e., identifiers for any numerical sequence as linear convolutions of a digital array. These indices are a sequence of matrix sums with matching row and column numbers obtained by vector multiplying a given digital array by its transposition. And they can be much smaller in volume than with conventional indexing.

At the same time, the index search process takes place in parallel, which ensures that it is accelerated many times. For example, an image is described as a matrix |X| with a number of pixels n = 1024 and a number of weight levels k = 10.

Let us define the vector product of the matrix |X| on its transposition |X|T as index I. I = |X| × |X|T = |Σ| = Σ00, Σ11, Σ22, Σ33, Σ44, … Σ99:

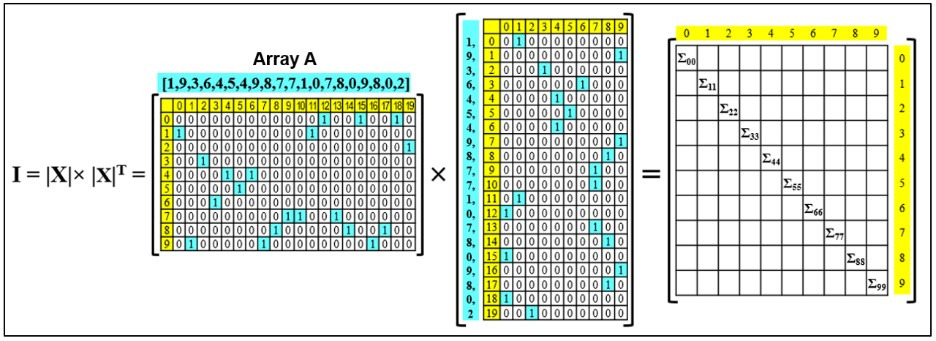
The length of the resulting index is equal to the number of weight levels and does not depend on the number of pixels in the images. Thus, if you set the standard number of weights to 10 (which is convenient because it corresponds to the accepted decimal system), these indices will be standard for all libraries, allowing them to be used universally.

Each image in the recognition libraries must be provided with an index. The recognition of each new image should begin with forming its index, allowing for quick recognition against the prepared libraries.

For example, suppose we use a decimal system (10 weight levels from 0 to 9); even if we limit ourselves to only the first significant digit of each sum, the index will be a combination of 10 single digits; the probability of random coincidences of indices will not exceed 10—10 (1/10 billion).

2.4.5. Similarity Patterns and Other Ways of Comparison and Indexing in BCF

Identifying patterns to understand and manage events is one of the most essential applications of neural networks.

Two images can be similar or appear similar to us for many reasons. Most often, similarity is determined by the common origin or manufacture of different objects or by the fact that different objects change and develop according to some general patterns, such as the laws of nature. Patterns in painting or music may be laws of composition, and the construction of machines may be formulas of material resistance science, customs, legal laws in society, etc.

An analogue of an object is another object with a high degree of similarity to this object. Analogy (similarity) can be general or particular, for a specific parameter, static or dynamic, complete or partial, etc. Any object can have a significant number of different analogues.

We described the recognition of images and the formation of search indices using similarity coefficients obtained through the vector product of image matrices. But that’s not the only option available with PANN. We have also tested other features, in particular, recognition through:

1. Matrix products of the input and comparison arrays on the array representing the “comparison standard” [Xst] and CoS calculations through the difference of the resulting matrix sums.

2. Characteristic sums of two arrays and calculation of CoS through the difference in the power spectra of the input and compared arrays.

3. Fourier transformation of the amplitude-frequency spectra of the input with compared arrays, and calculation of CoS through the difference or ratio of the BCF format harmonics lines of the same name.

Different types of recognition can be used together to improve the accuracy and reliability of the conclusion.

2.5. COMPARISON OF LIBRARIES AS A BASIS FOR RECOGNITION

Recognition on PANN networks is similar to recognition in the living brain.

Human memory is a vast library containing many objects and information related to these objects. At the same time, many objects are directly or indirectly connected by associative connections. When we see an object, we compare it with images in our memory and thus recognize it, for example, as a dog, a house, or a car. When we recognize an object and recall its closest analogues, we can transfer information from analogues to this object. In this way, we gain additional knowledge about the object, realize the possibilities of using this object or protecting ourselves from it, and so on.

PANN networks work similarly. Comparison libraries are formed in the computer’s memory, and recognition operates by comparing the received information with the information in these libraries according to the degree of similarity determined by similarity coefficients.

PANN comparison libraries consist of “memory units” whereby:

1. Each “memory unit” is a numerical sequence that can be written in graphical or text formats or a BCF format explicitly designed for PANN.

2. Each “memory unit” can be provided with its indices (public and private, in different details) so that the PANN network can quickly search libraries for information.

3. Each “memory unit” has a complex structure and contains data on different parameters and properties of the object. For example, when one of us says “airplane,” many airplanes come to mind, seen in real life or pictures, as well as knowledge about their design and application and the problems we have solved for Boeing and other companies.

4. Each “memory unit” has associative, programmatic, hypertextual, etc., connections with many other “memory units.” For example, I associate an airplane with a rubber-engine model that I built as a child, with the time I almost got into an air accident, with the terrorist attacks of September 11, 2001, etc.

5. Also, the “memory unit” can store crucial additional information, including information leading to understanding the process, emotional attitude, assessment of its usefulness, harmfulness, risks, etc.

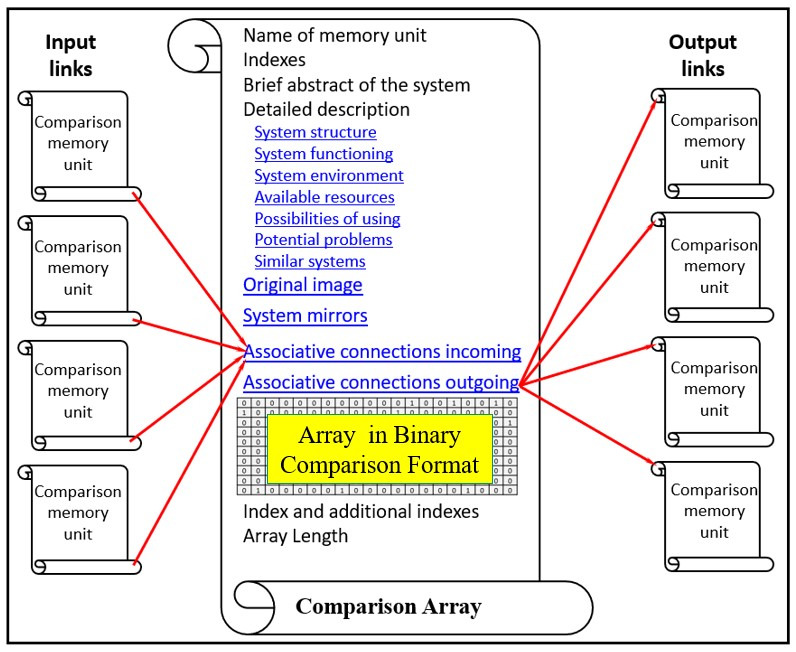
The memory library provides the identification of a particular object and, on its basis, the identification of close analogues or antagonist objects and the possibility of transferring information related to the found analogues to the identified object.

Each newly identified “memory unit” can be included in the comparison libraries, allowing the PANN to be continuously retrained.

2.6. FORMATION OF A NEURAL NETWORK BASED

ON PROGRESS NEURONS

New unique opportunities in the formation of a neural network.

In classical neural networks, the first step is to form a network structure of “empty,” untrained neurons and a random set of weights at synapses. Only then does the training of the prepared network begin.

In PANN, the situation is entirely different: you can train any number of neurons individually, train neurons in groups of five, ten, hundreds, or thousands of neurons, or prepare entire libraries in BCF format. Then, you combine everything you need to get a single network.

There are various designs of classical neural networks, many of which can be easily reproduced using the formal Progress neuron. Let’s examine the similarities and differences between the classical perceptron and the PANN network.

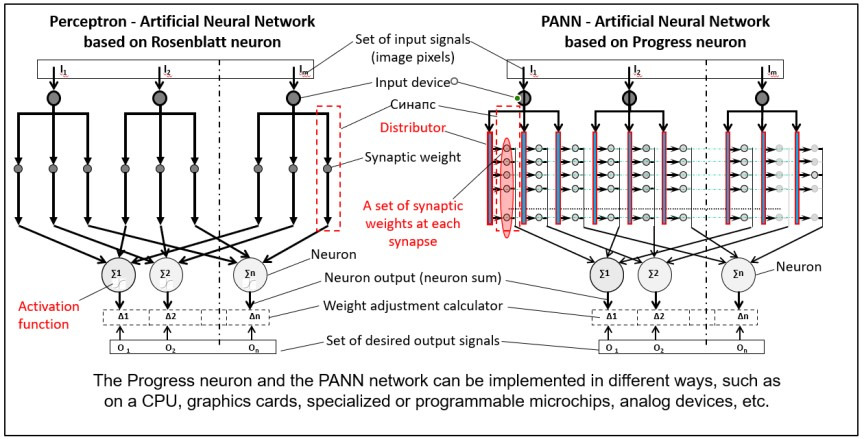
Fig. 11. Comparison of perceptron with PANN

When connecting neurons into a network, it is necessary to ensure the same number of inputs and the same number of weight levels for all neurons, which does not cause any difficulties. In principle, the format of the source data does not matter. When loaded to the network, it is automatically reformatted for the preselected number of number series members (number of inputs) and the specified number of weights.

Once the individual neurons, their groups and/or libraries are prepared, all the inputs of the same name (first, second, etc.) of all neurons are connected in parallel on the corresponding input bus. And all the outputs of neurons are sent to the “comparator” — the comparison module.

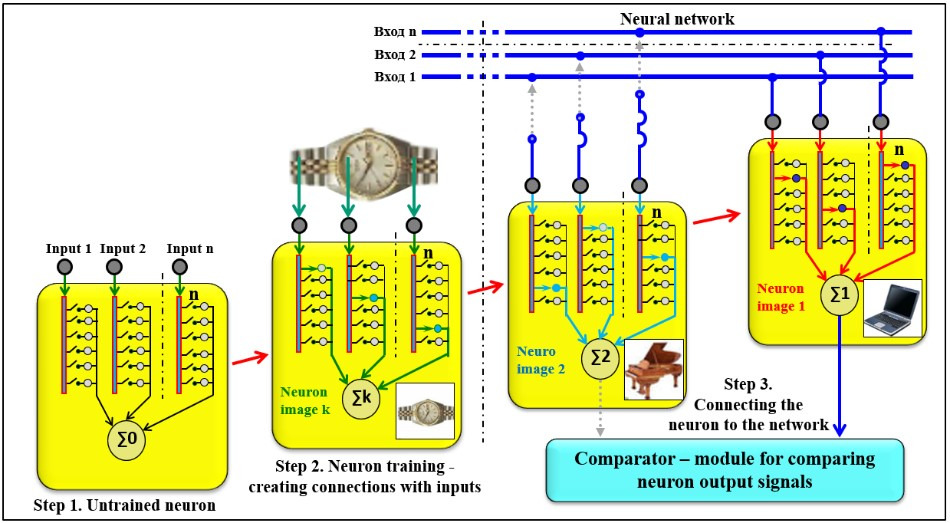
In the comparator, the operation |Xr| × |Xc|T proceeds — that is, the vector product of the matrix and the transposed matrix is determined |Xc|, where:

|Xr| — Recognized image matrix;

|Xc| — A matrix of the image to be compared.

Of course, it would take significant time to consistently multiply the recognizable image matrix by many comparative image matrices, so in actual software, all |Xc| (there can be hundreds, thousands, even millions of them if the computer is powerful enough) are assembled into a general (integral) matrix |Xc∑|.

Based on the results of this operation, the similarity coefficient between the matrix of the recognized image and each of the matrices of the compared images is determined. Based on the results obtained, a table of recognition results is built.

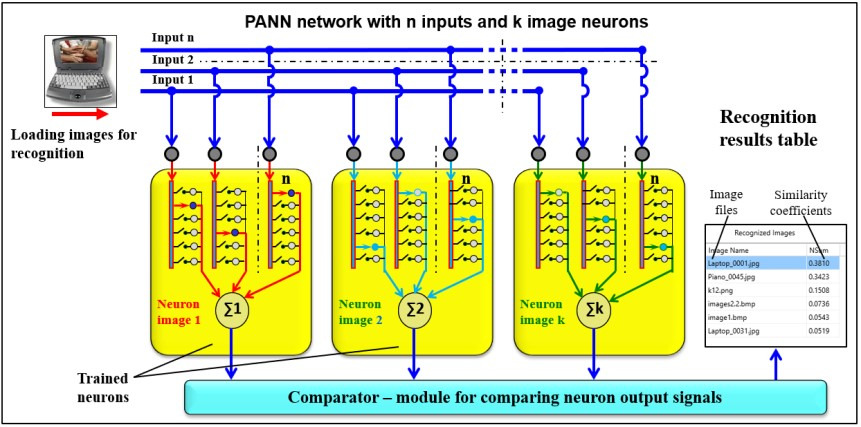
Fig. 13. Recognizing and constructing similarity ratings on a parallel PANN network

As the diagram shows, PANN networks are simply sets of image neurons. Therefore, they are dynamic and adaptive and can easily change and adapt to changing conditions, including when carrying out specific work.

One of the difficulties of working with classical neural networks is that most of the required useful functions cannot be implemented on a single-layer network. Many tasks require multiple layers of neurons. These networks are trained by backpropagation techniques, in which each layer significantly increases the computation required, resulting in a significant expenditure of time and energy.

In PANN, the situation is different. The independence of neuron-images from each other and the ability to train them separately make it possible to combine them in parallel, sequentially, or sequentially-parallel, build analogues of classical multilayer networks from simple single-layer networks, create “network committees,” generative-adversarial networks, and so on.

A multi-layer PANN is also possible, in which each layer can be a self-contained specialized filter. The training of this filter is independent of the other layers and, therefore, very fast.

2.7. CLUSTERING IN PANN

Creating generalized classes of images and then recognizing images related to these classes is the most popular application of neural networks. In classical networks, generalization requires many (often thousands and tens of thousands) images and complex and lengthy training. In PANN networks, generalization can be much easier with any number of images starting with 2. In this case, a generalized image of the class is recorded on one specialized “class neuron.”

2.7.1. Generalization (Class Formation) on the Progress Neuron

One of the most essential logical operations of the human mind is abstraction. In neural networks, this operation corresponds to the convolution and generalization of information, highlighting the most critical elements.

Generalization in PANN refers to forming an arithmetic mean (or, in some cases, geometric mean), two or more numerical sequences of the same length. The resulting “generalized images” can be easily visualized.

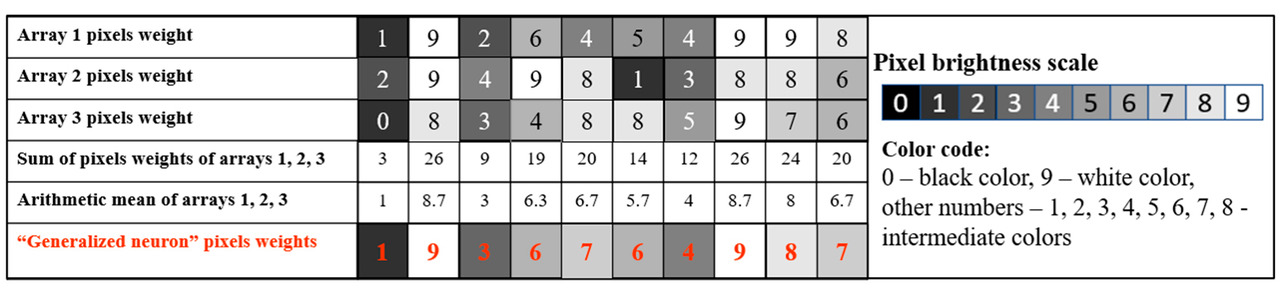
Fig. 14. Generalization and visualization of a generalized numerical sequence

Visualization of generalization processes allows you to see how similar features are strengthened and the “specific features” of the pictures disappear. This manipulation is a double-edged sword. Excessive generalization leads to the fact that this class includes images that are very different from each other. And the lack of generalization discards many pictures that should have made it into the class. This task in PANN is accomplished by creating a set of classes and subclasses of two or more levels.

Бесплатный фрагмент закончился.

Купите книгу, чтобы продолжить чтение.