
Бесплатный фрагмент - Организация и математическое планирование эксперимента
Учебное пособие
ВВЕДЕНИЕ
Большинство сложных научных задач проблемно решить без проведения физического или вычислительного эксперимента. Правильное, научно обоснованное, планирование эксперимента обеспечивает высокую точность, достоверность и адекватность результатов, а также может существенно сэкономить время на решение задачи. Поэтому будущий инженер-исследователь должен иметь достаточные представления о методах планирования эксперимента и обработки экспериментальных данных.
В данной книге максимально сжатым образом представлены основные теоретические данные, которые позволят правильно спланировать эксперимент, провести его и обработать полученные результаты. Опущены сложные выкладки с редко применяемой на практике теорией, при желании их можно найти в специализированной литературе.
В каждом разделе присутствуют подробные примеры использования алгоритмов обработки экспериментальных данных.
Учебное пособие снабжено заданиями на самостоятельную проработку, вопросами для самоконтроля и необходимыми справочными материалами.
1. Основы экспериментальных исследований
§1. Понятие эксперимента
Эксперимент наряду с наблюдением, измерением и описанием относится к эмпирическим методам познания, что подразумевает практическое изучение реально существующих и доступных объектов исследования или их моделей. Большинство практических научных исследований реализуется в виде эксперимента. Именно разработка теоретических основ экспериментальных исследований дала тот толчок развитию науки и техники, результат которого мы и наблюдаем сейчас.
Эксперимент — это последовательность действий, направленных на получение информации об объекте исследования путем контролируемых воздействий на него в воспроизводимых условиях.
Объектом исследования (ОИ) обычно выступает технологический процесс, о котором требуется получить необходимую информацию. Наиболее часто это экспериментальная информация о реакции объекта исследования на изменение внешнего воздействия. В этом случае эксперимент проводится для улучшения (или оптимизации) показателей работы технологического агрегата с целью повышения производительности и/или качества производимой продукции, уменьшения себестоимости и т. д.
Предмет исследования является определенной частью объекта исследования, это могут быть его отдельные свойства, особенности и т. д.
Воздействия на объект производится в виде опытов.
Опыт — это воспроизведение исследуемого процесса в лабораторных или промышленных условиях с регистрацией его результатов.
Последовательность действий при проведении эксперимента включает в себя следующие шаги:
— выбор объекта исследования, установление целей, определение факторов, влияющих на объект, а также откликов, которые будут контролироваться, составление плана проведения эксперимента;
— проведение всех предусмотренных планом опытов и регистрация результатов;
— выбор необходимой методики обработки экспериментальных данных, и их анализ с получением всей необходимой информации;
— подготовка и реализация нового экспериментального исследования, если это необходимо.
§2. Факторы, отклики и требования к ним
В ходе любого эксперимента стоит задача установить наличие и вид статистической связи между факторами и откликом.
Фактором называют входную величину, которая воздействует на ОИ, т.е. управляет его поведением и вызывает определенную реакцию на ее изменение. Фактор принимает в некоторый момент определенное значение, которое называют его уровнем.
Обычно фактор обозначают латинской буквой Х, если их несколько то к букве добавляют номер фактора Х1, X2, X3 … Xn,
К факторам предъявляют следующие требования:
— факторы должны быть управляемыми, т.е. исследователь в любой момент должен иметь возможность установить необходимый уровень фактора из плана эксперимента.
— факторы должны быть независимы друг от друга, т.е. уровень одного фактора не должен быть зависим от того на каком уровне находится другой фактор. Например, при исследовании процессов деформации брать в виде факторов одновременно температуру и сопротивление деформации, поскольку последнее зависит от первой. Поэтому необходимо использовать только один из них. Если это будет температура, то вторым фактором можно добавить, например, еще и скорость деформации.
— факторы должны быть совместимыми, т.е. комбинации их уровней возможно реализовать на практике (позволяет оборудование и технологический процесс) и они должны быть безопасными (сочетания факторов не должны приводить например к аварии, взрыву).
Факторы делятся на такие группы:
— контролируемые и управляемые — это факторы, уровень которых можно и измерить, и установить в любой момент времени на нужное значение (напряжение, расход газа и т.д.).
— контролируемые, но неуправляемые факторы — это факторы, величину которых можно измерить, но установить конкретный уровень невозможно (температура окружающей среды, влажность);
— неконтролируемые и неуправляемые — это факторы, уровни которых невозможно измерить или даже предугадать наличие самих факторов (износ механизмов, усталость металла, стресс у оператора механизма).
Отклик (еще можно встретить термины: параметр, реакция) — выходная величина на значение которой влияют факторы. Отклик обозначают латинской буквой Y.
Функция отклика — это уравнение, которое характеризует математическую связь между откликом и факторами
Таким образом в результате обработки экспериментальных данных на выходе необходимо получить подобную функцию отклика: y=f (x1, x2, … xn)
§3. Виды экспериментальных исследований
Экспериментальные исследования можно разделить на виды по нескольким признакам (рисунок 1.1).
По характеру получаемых результатов различают качественный и количественный эксперимент.
В результате качественного эксперимента устанавливается только сам факт наличия и направление влияния факторов на отклик, но количественные результаты исследования не приводятся и математическую модель не получают. Например, можно просто установить, что повышение скорости разливки на машине непрерывного литья заготовок приводит появлению дефекта «ромбичность», но не оценивать степень этого влияния.
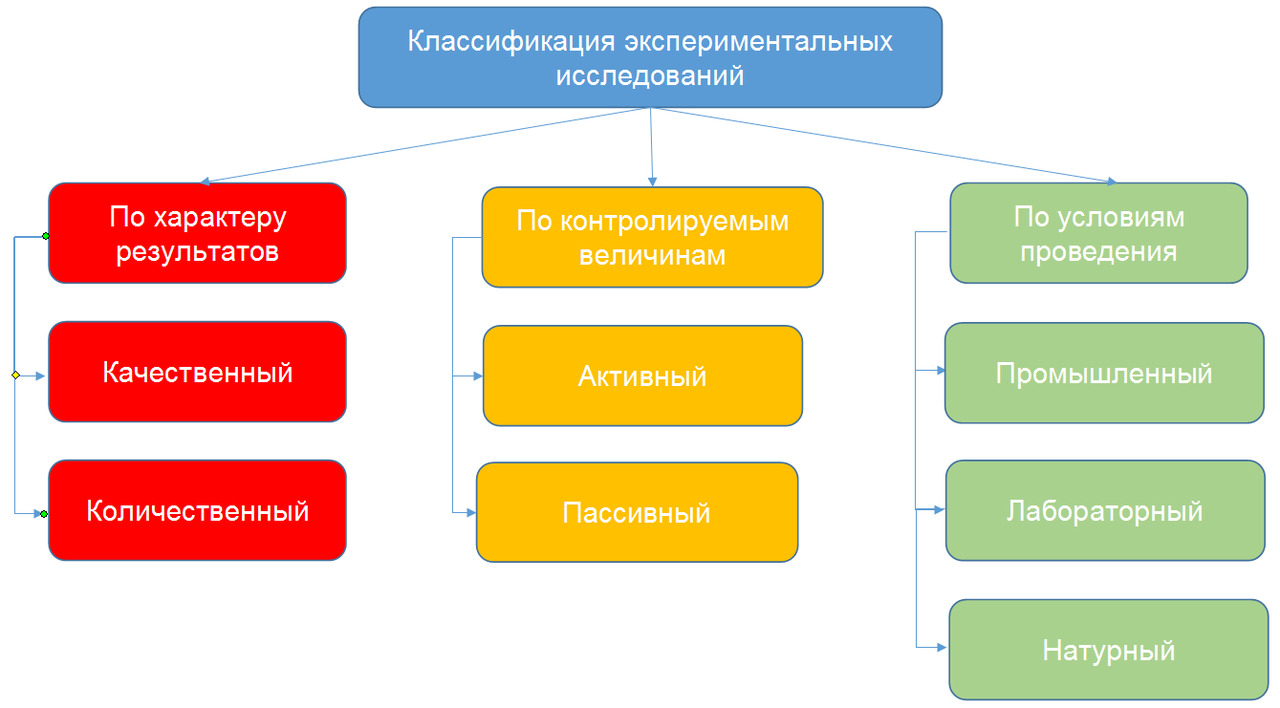
Количественный эксперимент подразумевает получение математической модели связи между факторами и откликом или хотя бы количественную ее характеристику. Например, можно установить математическую зависимость между количеством металлолома в завалке дуговой электросталеплавильной печи и удельным расходом электроэнергии на плавку.
По степени контроля за процессом эксперимент делится на активный и пассивный.
Если исследователь выполняет только роль наблюдателя, то эксперимент называется пассивным. Так как отсутствует возможность (или необходимость) в управлении уровнями факторов, и выполняется только измерение их величины. Также о пассивном эксперименте можно говорить, если выполняется статистическая обработка уже имеющихся данных за какой-либо период.
Активный эксперимент производится путем прямого вмешательства исследователя в изучаемый процесс, т.е. управление уровнями факторов, которое должно выполняться по разработанному плану эксперимента.
По условиям проведения различают промышленный, лабораторный, натурный, полевой эксперименты и т. д.
По характеру взаимодействия с объектом исследования различают материальный, вычислительный и мыслительный эксперименты.
Материальный эксперимент предусматривает работу исследователя непосредственно с натурным объектом исследователя или с его физической или аналоговой моделью.
Вычислительный эксперимент предполагает работу не с самим объектом исследования, а с его математической (чаше всего компьютерной) моделью. В настоящее время для вычислительных экспериментов в технике наиболее часто используется метод конечных элементов.
Мыслительный эксперимент реализуется в сознании исследователя, и часто предполагает предварительную проработку плана реального эксперимента. Можно сказать, что мыслительный эксперимент — это наиболее часто встречающая форма эксперимента, поскольку каждый из нас пытается в уме просчитать возможные варианты последствий перед ответственными действиями. В результате мысленного эксперимента может и отпасть необходимость в проведении материального. Однако у мыслительного эксперимента отсутствует строгий план действий.
По сфере приложения эксперименты можно разделить на физический, технологический, психологический, социометрический, экономический и т. д.
Пример. Допустим необходимо найти зависимость между температурой посада металла в нагревательную печь и временем нагрева до требуемой температуры. В этом случае в качестве отклика выступит время нагрева, а в качестве факторов непосредственно температура посада металла в печь и расход газа (или электроэнергии). Данные факторы будут относиться к управляемым и контролируемым. К неуправляемым, но контролируемым факторам можно отнести, например, температуру поступающего воздуха для горения в печи, химический состав газ (или напряжение в сети). К неконтролируемым и неуправляемым — состояние кладки в печи и прочие тепловые потери.
Задание на самостоятельную работу
Для технических процессов получения чугуна, выплавки стали, внепечной обработки стали, непрерывной разливки металла, нагрева заготовок в методических печах прокатки листового и сортового металла, волочения, прессования, или отдельных элементов этих технологий:
1. Указать возможные виды эксперимента для изучения процесса.
2. Определить факторы процесса, указать к какой группе они относятся, предположить уровни и пределы варьирования.
3. Указать отклики эксперимента.
Контрольные вопросы для самопроверки
1.Дайте определения понятиям: эксперимент, объект исследования, предмет исследования, опыт, фактор, отклик, функция отклика.
2. Назовите и раскройте основные требования к факторам.
3. На какие группы делятся факторы, охарактеризуйте их.
4. По каким признакам выполняется классификация экспериментальных исследований? Назовите основные виды эксперимента и раскройте их сущность.
2. Случайная величина. Функции и законы распределения
§1. Понятие о случайной величине
Поскольку в ходе проведения эксперимента исследователю приходится иметь дело с неконтролируемыми и неуправляемыми факторами, а измерение контролируемых производится с некоторой погрешностью, то и результаты эксперимента будут иметь носить характер (как бы это странно не звучало на первый взгляд). Это приводит к необходимости объемной и строго регламентированной обработки экспериментальных данных с использованием методов теории вероятностей и математической статистики.
Случайная величина — это величина, которая в результате проведения опыта принимает то или иное возможное значение. Это значение будет лежать в определенном интервале и не известно заранее.
Случайные величины делятся на дискретные и непрерывные.
Дискретной называют случайную величину, которая может принимать счетное количество значений из конечного или бесконечного множества значений. Часто этими значениями выступают целые числа, которые показывают число наступивших случаев. В качестве примера дискретной случайной величины можно представить число людей в цеху. Оно не может быть меньше 0 и не может быть сильно больше чем число работающих в цеху по штату, (например — 200 человек). Таким образом в течении рабочего дня данная случайная величина будет принимать разные значения, но они будут целыми числами из определенного конечного множества и их можно будет посчитать. Множество значений может быть и бесконечным, например, если отсчитывать количество поступающий на стан заготовок без брака до первого его появления. В этом случае данное количество может быть бесконечным (теоретически брак может так и не появиться), но при этом сосчитать все эти заготовки до появления брака возможно.
Непрерывной называют случайную величину, значения которой полностью заполняют конечный или бесконечный числовой промежуток. Таким образом, непрерывная случайная величина может принимать бесконечное число значений. Примером может служить измерение температуры в печи. Интервал значений в этом случае будет конечным (например, 20…1250 °С), а вот число значений величины может быть бесконечным, с учетом количества знаков после запятой. Непрерывной случайной величиной будет и цена на металл, которая определяется рыночной ситуацией и постоянно колеблется, принимая разные значения. В этом случае пределы цены теоретически ничем не ограничены.
§2. Функция и закон распределения
Полученные в результате измерений значения случайной величины распределяются по определенному закону. Закон распределения случайной величины устанавливает связь между полученными значениями случайной величины и вероятностями их появления. Вид этого закона распределения является одной из характеристик случайной величины.
Допустим произведено n измерений случайной величины X и получены значения х1, х2 … хn. При этом если речь идет о дискретной случайной величине, то она примет определенные значения случайное число раз, обозначим это число m. Если речь идет о непрерывной случайной величине, то весь диапазон ее изменения разбивается на несколько интервалов и подсчитывается количество попаданий в каждый из интервалов. Вероятность того что дискретная величина примет какое-либо значение (или попадет в определенный интервал) в этом случае будет:
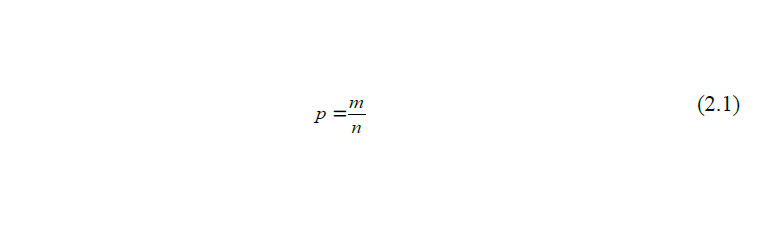
где m — число наблюдений, в которых дискретная случайная величина X оказалась равна x; n — общее количество наблюдений.
Сумма вероятностей всех возможных значений дискретной случайной величины (или попаданий во все интервалы для непрерывной) равна единице.
Для оценки распределения случайной величины используют функцию распределения и плотность распределения.
Функция распределения F (x) — это интегральная функция, которая показывает вероятность того, что случайная величина Х принимает значение не больше, чем х:
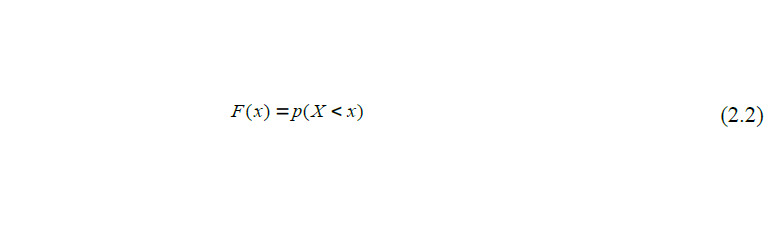
Функция распределения должна иметь возрастающий характер.
Плотность распределения f (x) — это дифференциальная функция — производная функции распределения, которая определяется как:
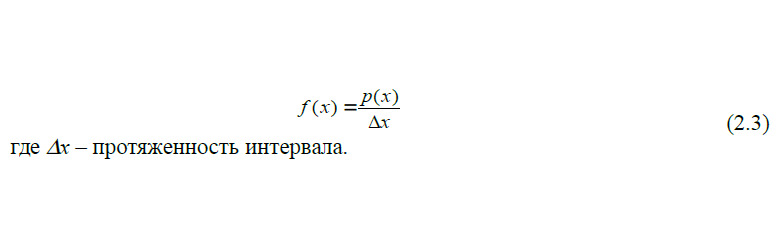
Для правильной обработки экспериментальных данных необходимо знать закон распределения, однако для его точного определения необходимо обработать большой объем экспериментальной информации.
Пример. На предприятии выпускается проволока различных диаметров. Отдел товарного контроля производит периодические замеры диаметра готовой проволоки. Результаты измерения (всего 50) проволоки диаметром 3,6 мм находятся в таблице 2.1. Значения диаметра проволоки отличаются друг от друга из-за того, что проволока производится в пределах допусков и диаметр может отличаться как в большую, так и в меньшую сторону и это не является нарушением технологии, также на результаты может влиять погрешность измерений.
Таблица 2.1 — Результаты замеров

Дальнейшую обработку данных ведем по следующей методике.
Для удобства необходимо отсортировать данные по порядку от большего к меньшему — таблица 2.2.
Для непрерывной случайной величины задают вероятность ее попадания в один из заданных интервалов области ее определения (поскольку вероятность того, что она примет какое-либо конкретное свое значение, стремится к нулю).
Таблица 2.2 — Упорядоченная таблица результатов замеров

Количество интервалов определяют по формуле
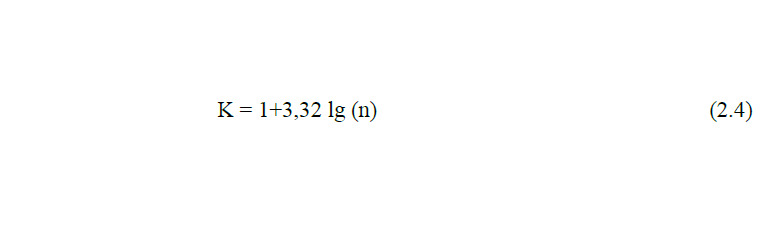
где n — количество измерений.
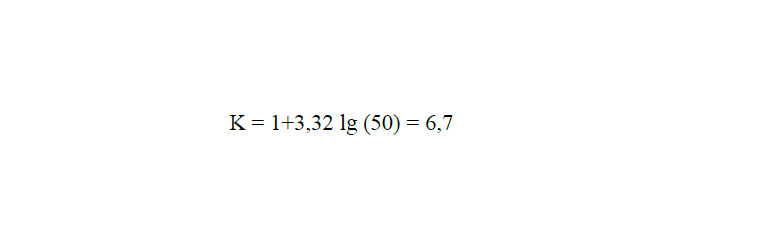
В качестве количества интервалов принимаем большее нечетное число — 7.
По таблице 2.2 определяем наибольшее и наименьшее значение хmin = 3,4, хmax = 3,8, диапазон изменений (размах) случайной величины Lx = 3,8 — 3,4 = 0,4. Тогда продолжительность каждого из семи интервалов Δх = 0,4/7 = 0,057. Значение продолжительности интервала достаточно округлить на порядок больший, чем точность измерений случайной величины.
Таким образом, получим семь интервалов, границы которых приведены в таблице 2.3.
Теперь подсчитаем сколько раз случайная величина попала в каждый из интервалов, обозначим это значение — m, и частотную вероятность попадания в каждый интервал по формуле 2.1.
Например в интервал 3,4…3,457 попадает всего два значения из таблицы 2.2 — это 3,4 и 3,45, частотная вероятность в этом случае будет: р = 2/50 = 0,04, результаты для остальных интервалов приведены в таблице 2.3. Сумма всех вероятностей должна быть равна единице.
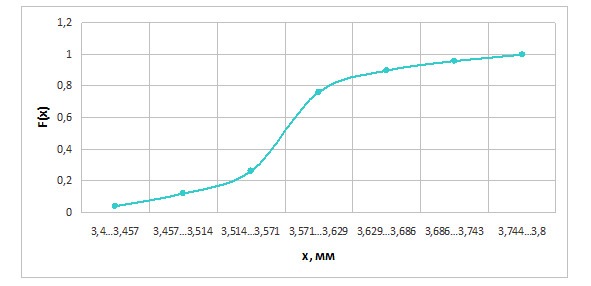
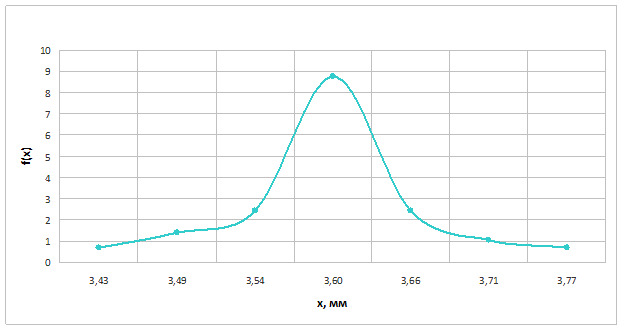
Для построения функции распределения необходимо определить сумму всех вероятностей с начала интервала до требуемого значения. Т.е. ее значение для второго интервала 0,04+0,08 = 0,12, для третьего 0,04+0,08+0,14 = 0,26 и т. д. Последнее значение всегда должно быть равно 1. График интегрального закона распределения (функции распределения) приведен на рисунке 2.1.
Таблица 2.3 — Данные для определения вида закона распределения
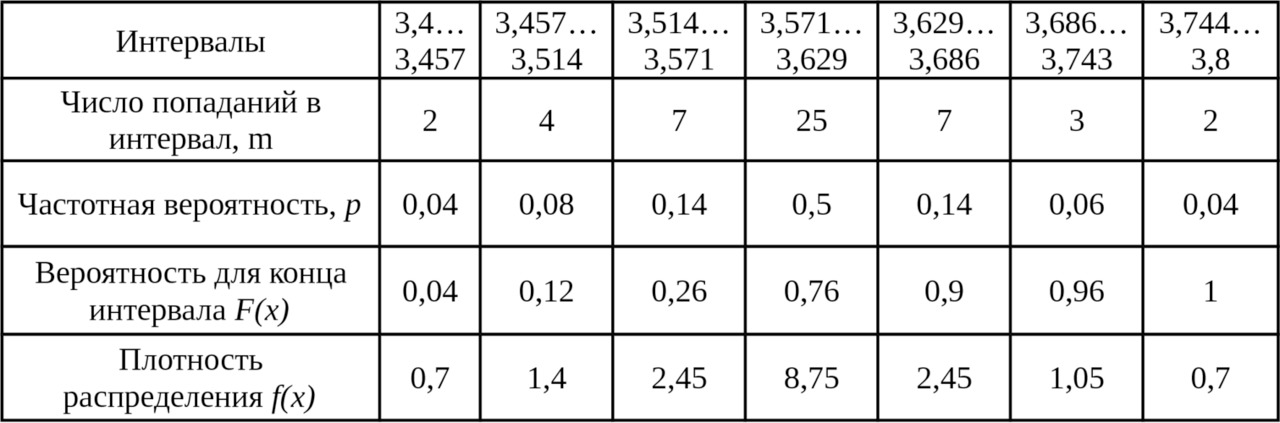
По формуле (2.3) рассчитываем плотность распределения для каждого из интервалов. Например для первого она равна p = 0,04/0,057 = 0,7. Аналогично и для остальных интервалов, результаты приведены в таблице 2.3
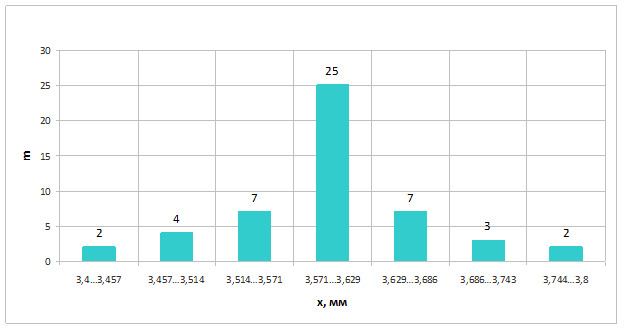
При построении графика дифференциального закона распределения (плотности распределения), который приведен на рисунке 2.3, надо учитывать, что абсциссы точек должны располагаться посередине каждого интервала, а ординаты будут соответствовать значению f (x) в указанном интервале.
Предварительно вид закона распределения можно определить и по внешнему виду гистограммы распределения, которая приведена на рисунке 2.3.
Для дискретной случайной величины в том случае если она принимает небольшое количество значений, интервалы между которыми одинаковы (например она принимает только значения 3, 4, 5, 6, 7, 8, 9) то можно рассчитывать вероятность того что случайная величина примет конкретное значение, в этом случае продолжительность интервала Δх = 1. В обратном случае необходимо также производить разбивку на интервалы. Все остальные вычисления проводятся аналогично.
Большинство полученных в ходе экспериментальных исследований распределений случайной величины подчиняется определенным законом, которых существует достаточно большое количество. Все эти законы распределения имеют критерии, по которым можно установить принадлежность распределения случайной величины к одному из законов.
§3. Нормальный закон распределения
Если влияние неуправляемых и неконтролируемых факторов на значение случайной величины небольшое, а все факторы, которые сильно воздействуют на отклик в ходе эксперимента обязательно контролируются, то распределение случайной величины будет подчиняться нормальному закону распределения. Такое распределение называют еще и Гауссовским распределением.
В случае, если случайная величина распределена по нормальному закону распределения, то график плотности распределения будет иметь пик в центре, который соответствует среднему значению случайной величины, а сама кривая будет симметрична относительно центра и принимать форму колокола (рисунок 2.4.).
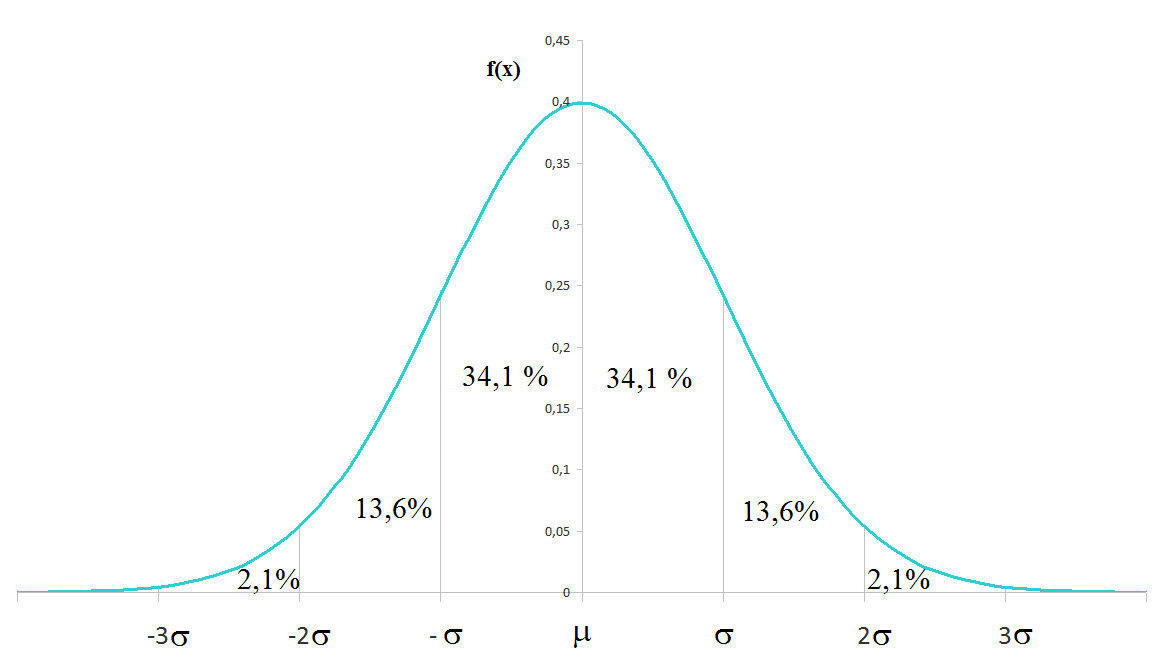
Из рисунка 2.4 также следует, что нормально распределенная случайная величина попадает с вероятностью 0,997 в интервал от 3σ до +3σ это правило носит названия правила трех сигм.
Если в результате измерений случайная величина будет распределена не по нормальному закону, а например по равномерному (при котором она попадает во все интервалы примерно одинаковое число раз), то это может говорить о том, что какой то фактор, который существенно влияет на измеряемую величину не учтен, и следует пересмотреть постановку эксперимента. Также это может происходить в том случае, когда значения величины в реальности не контролируются, а записываются в отчет случайным образом (например, до датчика, установленного на промышленном агрегате долго идти или сложно добраться, а контролирующему лицу лень это делать).
§4. Определение вида закона распределения
Определить, к какому из закон распределения относится закон распределения измеренной величины, можно или графическим способом, построив график плотности распределения и сравнив его форму и отклонения величин с эталонным графиком данного вида распределения, или с помощью различных расчетных методик.
К одной из таких методик относится методика определения вида закона распределения с помощью критерия Пирсона.
Она заключается в сравнении значений распределения полученного путем измерений на практике с теоретическим значениями предполагаемого закона измерения.
Таким образом, вначале необходимо обработать измерения по методике приведенной в §2, построить график плотности распределения и по его внешнему виду высказать предположение о виде закона распределения. Затем рассчитать в дополнение к имеющимся практическим вероятностям попадания значения случайной величины в определенный интервал, теоретические значения и сравнить их.
Рассмотрим подробнее методику проверки принадлежности распределения случайной величины, к какому либо закону распределения.
По методике, описанной в §2 определяют количество измерений n, количество интервалов k, и количество попаданий значений случайной величины в каждый из интервалов — mi (где i=1…k). Следует отметить, что для корректного анализа с помощью критерия Пирсона необходимо наличие в каждом интервале хотя бы 5 значений. В противном случае интервалы с малым количеством значений надо объединить с соседними. Далее в соответствии с теоретическим законом распределения рассчитывают теоретические вероятности попадания случайной величины в эти же интервалы — pтi.
Например, для нормального распределения зависимость для определения теоретических вероятностей будет выглядеть следующим образом:
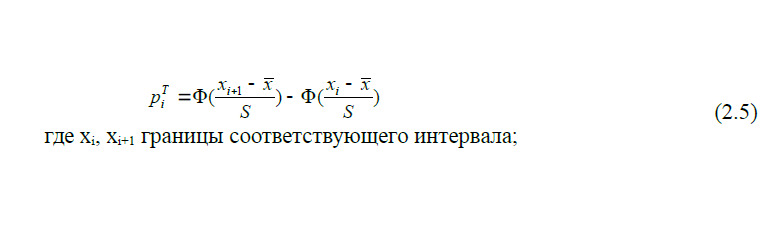
Следует особо подчеркнуть, что Ф (-х) = -Ф (х)
Для других законов распределения будут использоваться другие функции, которые можно найти в соответствующей литературе.
Табличное значение критерия Пирсона χ2табл определяется по приложению Б в зависимости от уровня значимости α и степени свободы f=k-r-1, где r — это число параметров распределения необходимое для расчета теоретических вероятностей по соответствующей ему аналитической функции (будет отличаться для разных законов распределения).
Расчетное значение критерия Пирсона определяется по формуле:
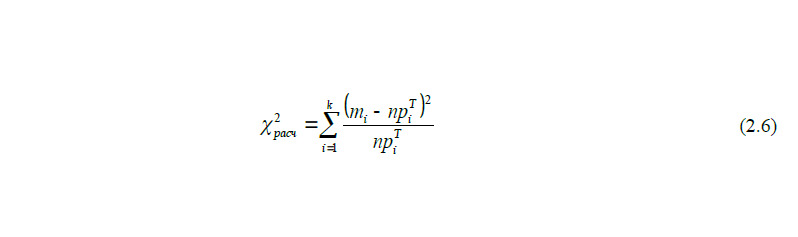
В случае когда χ2табл> χ2расч предполагаемый закон распределения принимается. В противном случае необходимо проверить другой закон распределения или увеличить количество измерений.
Пример. Для распределения, приведенного в примере §2, проверить его соответствие нормальному закону распределения.
Решение. Приведем необходимую часть таблицы 2.3.
Таблица 2.5 — Число попаданий в интервал

Как видим в двух из интервалов количество попавших в них значений меньше 5, поэтому объединим эти интервалы с соседними (см. таблицу 2.6)
Таблица 2.6 — Число попаданий в интервал

Всего было произведено n=50 замеров.
Параметры распределения определяем по формулам (4.1, 4.3): xcp = 3,6; S=0,071
Рассчитаем теперь теоретические вероятности, значения функции Лапласа берем из таблицы в приложении Е:
для первого интервала
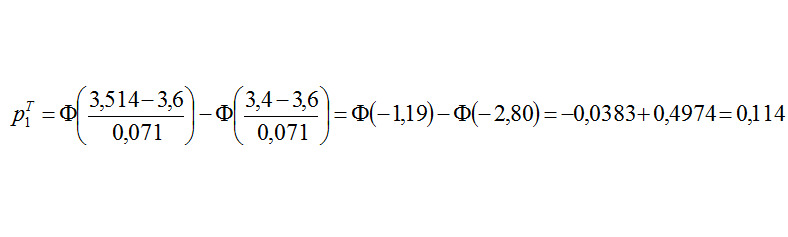
для второго интервала
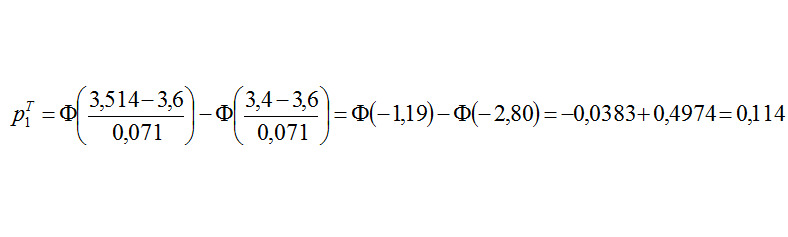
Аналогично для следующих:
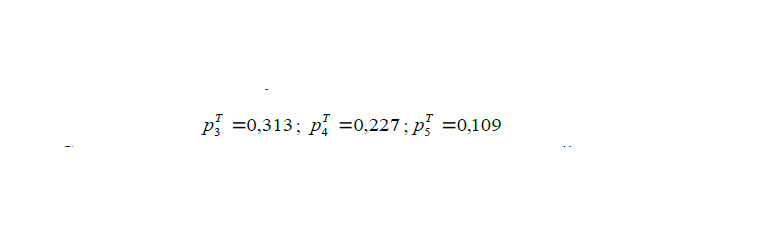
Сумма вычисленных теоретических вероятностей должна равняться единице.
Определяем расчетное значение критерия Пирсона по формуле (2.6):
Определяем табличное значение критерия Пирсона для α=0,05 и f=5—2—1=2 (r =2 потому что для вычисления теоретических вероятностей мы использовали два параметра распределения — среднее значение и среднеквадратичное отклонение)
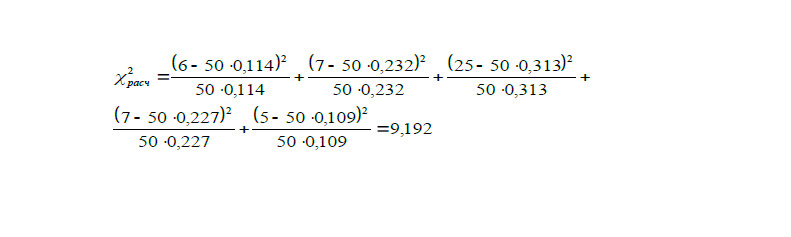
Таким образом, получаем, что χ2табл <χ2расч и закон распределения нельзя считать нормальным. Однако есть возможность уменьшить уровень значимости до α=0,1, в этом случае χ2табл = 9,2 и равенство χ2табл> χ2расч выполняется. Таким образом, можно утверждать, что с вероятностью 90% закон распределения случайной величины соответствует нормальному закону распределения.
Если увеличение уровня значимости не устраивает исследователя, то необходимо увеличить количество измерений n до 100 и более.
Задание на самостоятельную работу
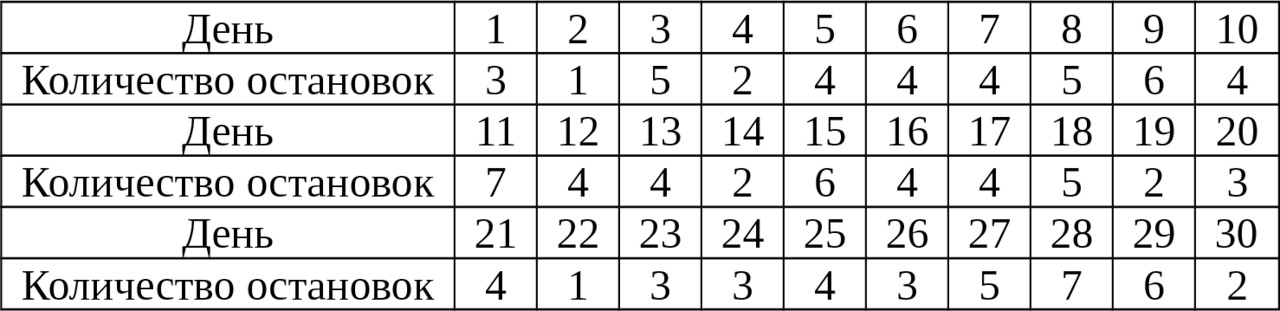
Произвести анализ представленных таблице 2.7 данных по представленной выше методике и определить тип закона распределения.
Таблица 2.7 — Количество остановок стана при нештатной ситуации в течении месяца
Контрольные вопросы для самопроверки
1. Дайте определение понятия «Случайная величина», почему результаты эксперимента необходимо обрабатывать как случайные величины.
2. Какие бывают случайные величины, в чем их отличия, приведите примеры.
3. Что такое функция и плотность распределения? Что необходимо для построения их графиков?
4. Что такое нормальный закон распределения? Назовите его основные признаки
5. Раскройте методику определения закона распределения по критерию Пирсона.
3. Основы планирования эксперимента
§1. Эксперимент как объект планирования
Планирование эксперимента является одной из первых и важнейших стадий его проведения и обуславливает весь дальнейший процесс. С помощью методов математического планирования эксперимента возможно решение следующих задач:
— определение минимального числа опытов, которые необходимы для получения адекватных результатов;
— установление порядка проведения опытов;
— получение математической зависимости отклика от факторов.
План эксперимента представляет собой таблицу, в которой указано количество опытов и значения уровней факторов в каждом из них.
Плану эксперимента должны быть присущи ортогональность, оптимальность и ротабельность.
Ортогональность плана эксперимента предусматривает возможность получения независимых друг от друга оценок коэффициентов регрессии, а также замену любого коэффициента без изменения оценок других.
Оптимальность плана эксперимента предусматривает получение оценок коэффициентов регрессии с максимальной точностью. В настоящее время известно боле 20 различных критериев оптимальности.
Ротабельность плана эксперимента предусматривает получение одинаковой точности предсказания значений отклика для равноудаленных значений факторов.
Для составления плана эксперимента зная минимальное (нижнее) и максимальное (верхнее) значение уровней каждого из факторов (должно быть определено на начальном этапе проведения эксперимента исходя из технологических и исследовательских соображений) необходимо определить для каждого из них нулевой или основной уровень Xi0 и интервал варьирования ΔXi переменных:
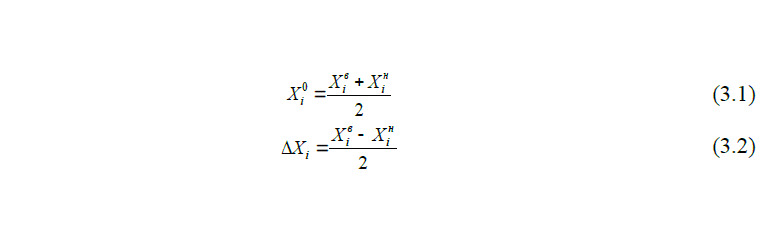
При математическом планировании эксперимента для приведения всех значений факторов в безразмерный вид выполняют кодирование размерных значения факторов Хi в безразмерные хi по формуле:
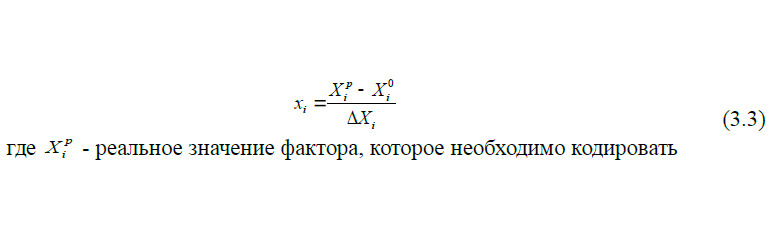
Кодовое значение — 1 будет соответствовать в этом случае нижнему уровню фактора, а +1 верхнему.
Если фактор берется на трех уровнях, то добавится еще и нулевое значение фактора, которое будет соответствовать основному уровню фактора. При четырех уровнях кодовые значения будут равны +2, +1, -1, -2. При пяти — +2, +1, 0, -1, -2 и т. д. Полученные таким образом кодовые уровни факторов заносятся в план-матрицу эксперимента в соответствии с правилами, которые будут рассмотрены ниже.
Далее необходимо произвести рандомизацию опытов, т.е. проводить их не в последовательности их номеров в плане эксперимента, а в случайном порядке.
Математическая зависимость отклика от факторов, так называемое уравнение регрессии, обычно ищется в виде полинома:
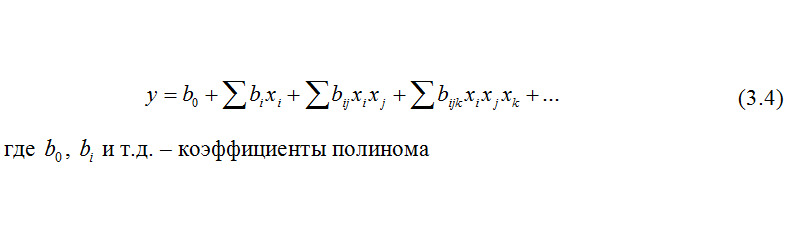
Коэффициент b0 — это свободный член, коэффициенты bi, которые стоят при переменных, соответствующих каждому фактору называются эффектами факторов, а bij, bijk и т.д., которые стоят перед перемножениями переменных, называются эффектами взаимодействия факторов.
В настоящее время разработано довольно много различных планов эксперимента и подходов к их составлению. Рассмотрим наиболее простые и распространенные из них.
§2. Полный факторный эксперимент
Полный факторный эксперимент предполагает реализацию в ходе опытов всех комбинаций уровней всех факторов между собой. Количество опытов при этом будет максимально и равно:
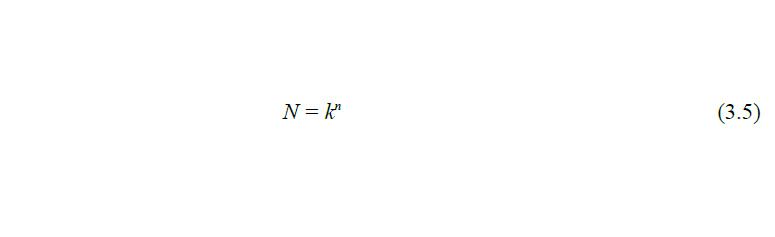
где n — количество факторов
k — количество уровней.
План-матрица эксперимента заполняется по простым правилам:
— для первого фактора в столбик записываются чередования всех уровней от меньшего к большему, т.е. чередуются уровни -1, +1, или -1, 0, +1 и т. д.
— для второго фактора записывают подряд в столбик столько одноименных значений уровня фактора, сколько насчитывается его уровней, т.е. для двух уровней -1, -1, +1, +1, для трех -1, -1, -1, 0, 0, 0, +1,+1, +1 и т. д.
— для третьего уже записываются подряд в столбик равное квадрату количества его уровней количество одноименных значений уровня фактора: для двух факторов -1, -1, -1, -1, +1,+1,+1,+1, для трех по девять, и т. д. для остальных факторов.
Не стоит забывать, что сумма любого из столбцов в итоге всегда должна быть равна нулю.
Рассмотрим теперь данные правила на примерах. Для простоты верхний (+1) и нижний (-1) уровни факторов будем обозначать просто знаками + и –.
План-матрица для самого простого эксперимента ПФЭ 22 (два фактора на двух уровнях) приведена в таблице 3.1.
Если уровней каждого фактора будет 3 то матрица расширится до 9 опытов (ПФЭ 32), а в уровни факторов добавится еще и 0 (см. таблицу 3.2).
Таблица 3.1 План-матрица ПФЭ 22
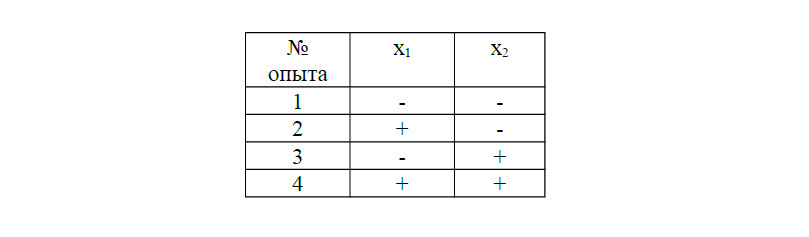
Таблица 3.2 План-матрица ПФЭ 32
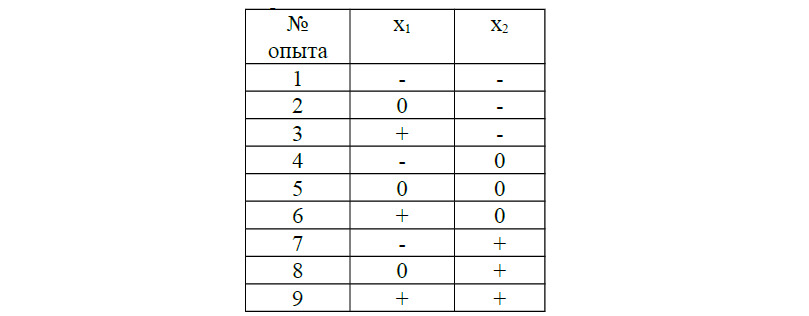
План-матрица для ПФЭ 23 (три фактора на двух уровнях) приведена в таблице 3.3.
Таблица 3.3 План-матрица ПФЭ 23
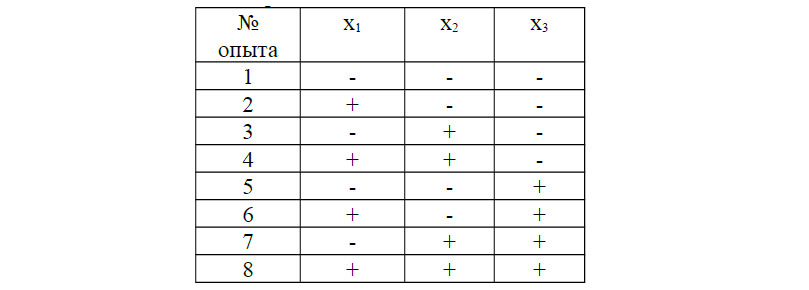
По аналогичным принципам составляются план-матрицы эксперимента для других количеств факторов и уровней. Следует отметить что существуют специальные справочники в которых приведены план-матрицы экспериментов для большого числа его видов.
Для последующего нахождения коэффициентов регрессии (подробно будет рассмотрено в главе 6) необходимо строить расширенную план-матрицу эксперимента в которую добавляются столбцы, которые соответствуют коэффициентам уравнения регрессии, которые необходимо найти, а также значение (среднее значение, если опыты повторяются) отклика.
Например для ПФЭ 23 уравнение регрессии с учетом (3.4) ищется в виде:
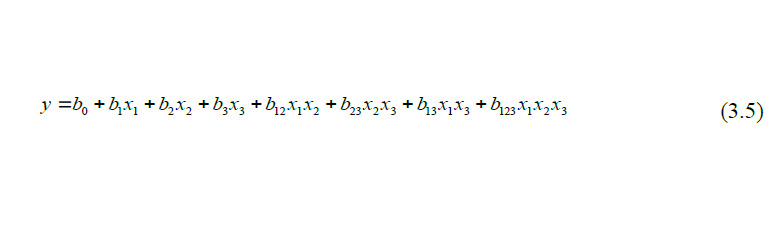
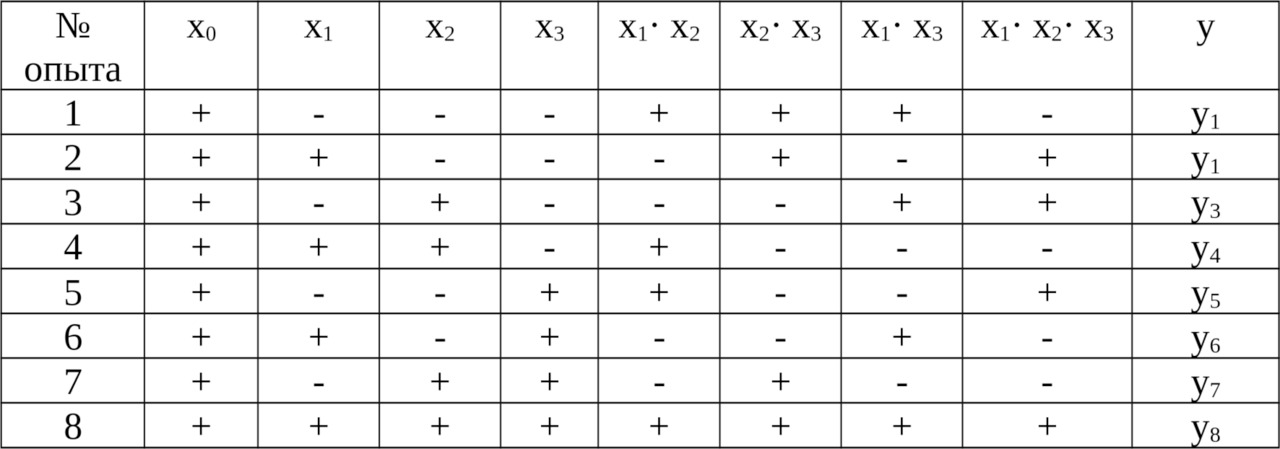
а в план-матрицу добавятся столбцы, приведенные в таблице 3.4
Таблица 3.4 Расширенная план-матрица ПФЭ 23
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
