Бесплатный фрагмент - Нотация туннельного моделирования для программистов

Введение

Наука только тогда достигает совершенства, когда ей удаётся пользоваться математикой.

К. Маркс

Человечество издавна ставило перед собой вопросы о соотношении частей знания, предлагаемого опытом предыдущих поколений и накапливаемого человеком во время воспитания, познания общества и технологий, воспитания своих детей. Ответы на вопросы записывались в книгах, передавались из поколения в поколение.

Автор предлагает рассмотреть ещё один вариант, основанный на исследовании жизнедеятельности предприятий. Подход включает в себя опыт классификации категорий философии, представлений о развитии технических и организационных систем.

В результате исследований появился вариант графической нотации элементов моделирования для описания мыслей в виде схемы на одном листе. Графические языки издавна оказывают помощь человечеству. Иероглифы появились на пирамидах Древнего Египта и до сих пор используются в Китае и Японии. При изучении физики используются схемы сил и электрических цепей. Для каждой области человек старается придумать наиболее содержательный язык. Вопросы построения онтологий рассматриваются при построении семантических сетей в интернете, при построении моделей технических систем.

В предлагаемой вниманию читателя книге предлагается подход, основанный на математике, для построения онтологий. При этом рассматривается возможность мировосприятия с позиции дуализма, предложенной Р. Декартом, — независимости и симметрии материального и абстрактного.

В настоящее время известно значительное количество методик анализа предметной области: стандарты группы IDEF, BPMN, UML. Добавление новой нотации вызвано исследованием по оценке положений терминов на сферической поверхности. Первые успехи позволили ввести систему обозначений для терминов, используемых при моделировании информационных систем.

Автор заранее извиняется за краткость изложения. Чтение не должно вызывать ощущения нудности. При этом автор надеется на то, что содержание сложных частей будет раскрыто другими авторами, и заранее приносит им свою благодарность.

Автор выражает огромную признательность знаменитым и не очень, в том числе ныне живущим авторам, чьи работы оказали влияние на формирование мировоззрения. Особенную благодарность хочется выразить А. Якобсону, Г. Бучу, Дж. Рамбо, описавшим самораскручиваемый процесс разработки программного обеспечения, П. Домингосу, ограничившему разнообразие развития пятью механизмами.

Для эпиграфа используется цитата с сайта http://kvm.gubkin.ru/mysli.html.

Для обложки использован фрагмент изображения с сайта http://terminometr.wallst.ru, URL изображения http://terminometr.wallst.ru/image/RainBowAll.png.

Обсуждение нотации моделирования возможно в следующих сообществах:

Facebook: https://www.facebook.com/groups/tunnelmodeling/;

ВКонтакте: https://vk.com/tunnelmodeling/;

Живой Журнал: https://tunnel-modeling.livejournal.com.

Все упоминаемые в тексте товарные знаки являются собственностью соответствующих фирм.

Дуализм Декарта

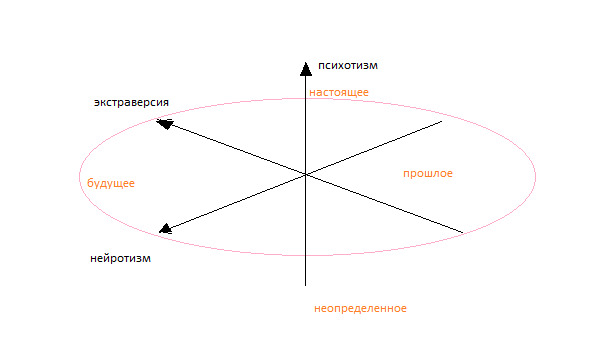
Основой подхода к построению служит предложенное Рене Декартом деление субстанций на «протяжённую» и «мыслящую», проще говоря, на природные явления и абстракции. Такое деление позволяет избежать споров о первичности — любая развитая цивилизация придёт к изобретению математики. Для привязки мировоззрения Декарта к координатам используются шкалы Г. Ю. Айзенка, рис. 1 (цитируется из URL https://philos-cafe-spb.livejournal.com/70022.html, URL рисунка https://ic.pics.livejournal.com/palex/22359553/29076/29076_original.png, проверено 20.04.2020).

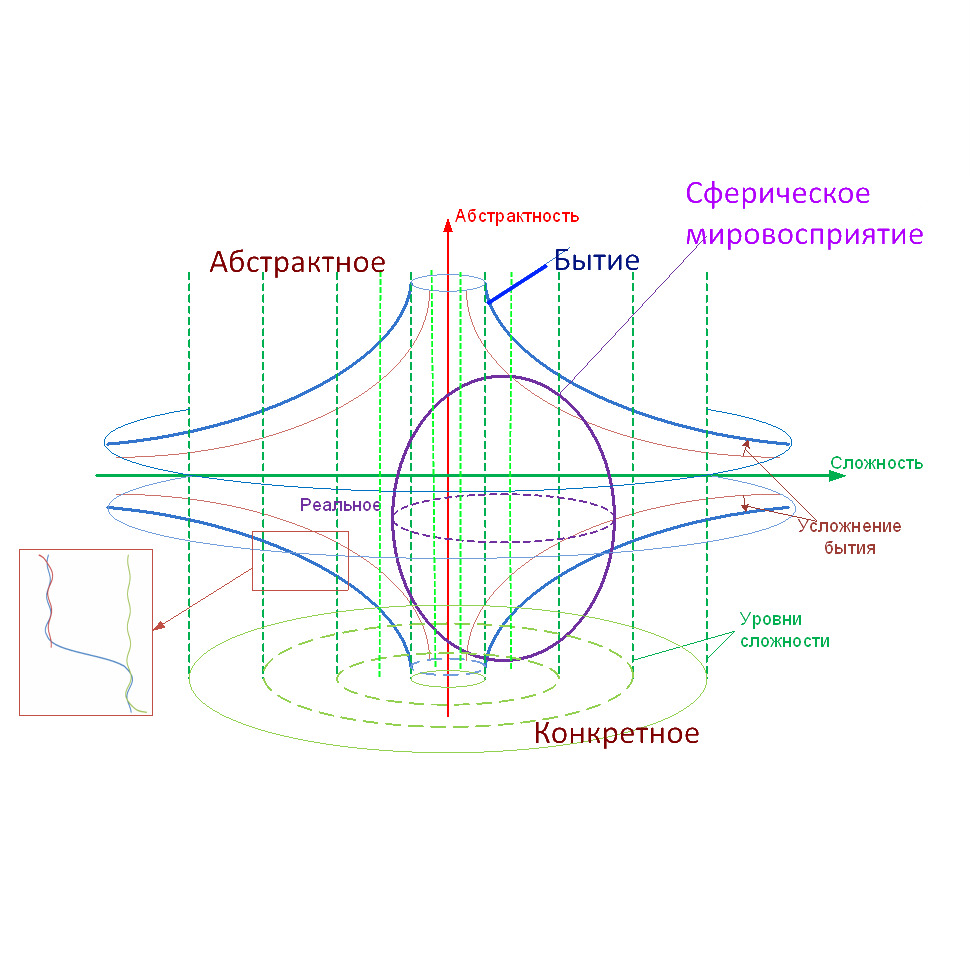
На рис. 2 показан вариант описания усложнения природы и общества с проекцией на сферическую поверхность мировосприятия (цитируется по «Туннельное моделирование — версия 0.9», рис. 10, URL: https://habr.com/ru/post/259291, URL изображения: https://habrastorage.org/getpro/habr/post_images/13a/9f8/f9d/13a9f8f9d41669faf26809d2ca3a143d.png, проверено 20.04.2020).

Сферическая модель мировосприятия

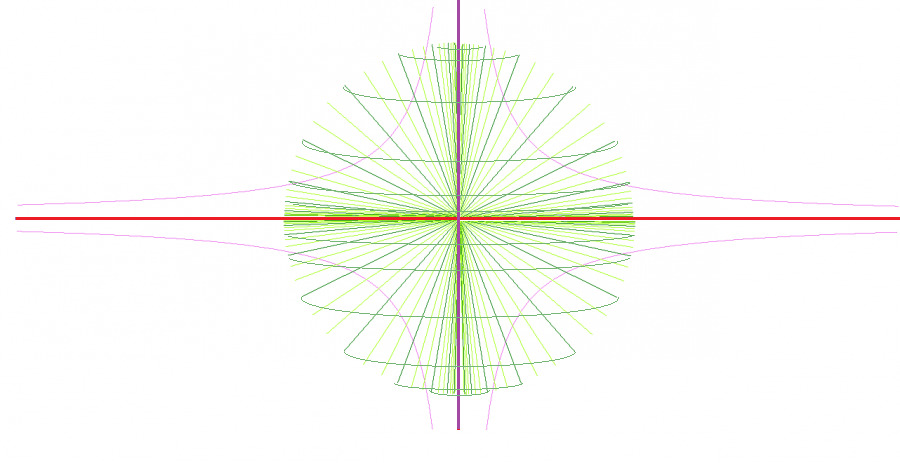
Для сферического мировосприятия вводится система координат, в которой угол между осью и направлением определяется через арккотангенс квадрата абсциссы. Данный подход позволяет ввести координаты, усложняющиеся от полюсов к экватору (цитируется по «Туннельное моделирование — версия 1.0», рис. 1, URL: https://habr.com/ru/post/414861/, URL изображения https://habrastorage.org/getpro/habr/post_images/de5/5ed/dca/de55eddca26a233f6d7cdab8dfd70d93.png, проверено 20.04.2020).

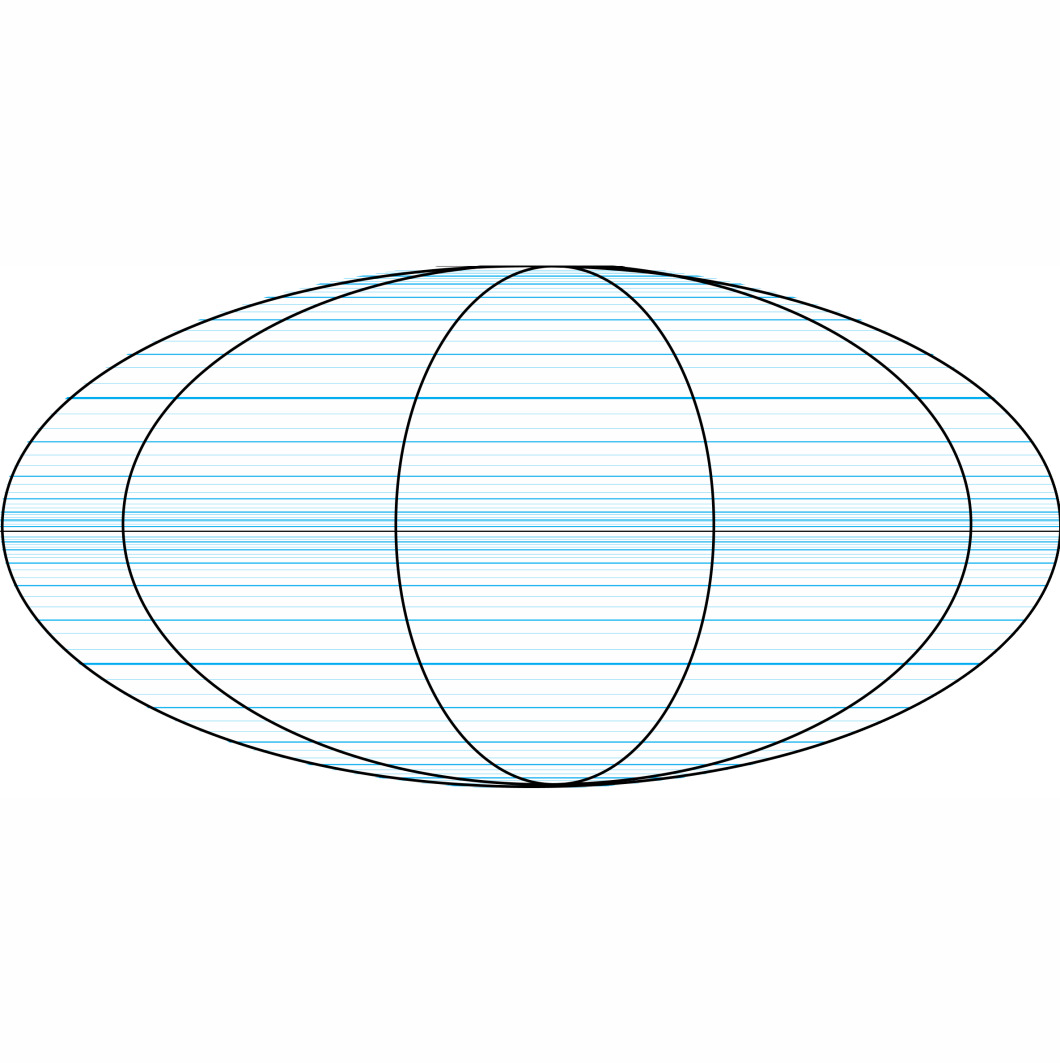
На рис. 4 показан вид координатной сетки, образованной проекцией гиперболической координатной сетки на сферу.