
МОДУЛЬ 1. АЛГЕБРА
В основной школе математическое образование состоит из основополагающих разделов: арифметика, геометрия, алгебра, элементы комбинаторики, теории вероятностей, статистики и логики. Все вместе они показывают богатый опыт изучения математики в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют выполнить поставленные перед школьным образованием задачи на информационном и логическом материале. Все содержательные компоненты, указанные выше, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Алгебра в нашей стране имеет особое значение для развития всесторонне развитой личности обучающегося.
Алгебра направлена на формирование математического аппарата, математического мышления для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры не похож на другие языки, однако основан на арифметических и математических действиях. Его мы используем для построения математических моделей, процессов и явлений реального мира (одна из основных алгебраических задач изучения предмета — развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений). Как и другие разделы математики, алгебра необходима для формирования у обучающихся представлений о роли математики в развитии культуры и цивилизации в целом.
Алгебра требует от обучающихся умственных и волевых усердий, концентрации внимания, активности развитого воображения, формирует нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения. Для контроля успешности овладения знаниями в курсе алгебры предусмотрены контрольные работы.
Предметными результатами изучения курса «Алгебра» в 9 классе является сформированность следующих умений (согласно ООП ООО):
Ученик научится:
— осознание значения математики для повседневной жизни человека;
— представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации;
— развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли с применением математической терминологии и, символики, проводить классификации, логические обоснования;
— владение базовым понятийным аппаратом по основным разделам содержания;
— систематические знания о функциях и их свойствах;
— практически значимые математические умения и навыки, их применение к решению математических и нематематических задач, предполагающее умения:
— выполнять вычисления с действительными числами;
— решать неравенства, системы неравенств;
— решать текстовые задачи с помощью составления и решения уравнений, систем уравнений и неравенств;
— использовать алгебраический язык для описания предметов окружающего мира и создания соответствующих математических моделей;
— проводить практические расчеты: вычисления с процентами, вычисления с числовыми последовательностями, вычисления статистических характеристик, выполнение приближённых вычислений;
— решать простейшие комбинаторные задачи;
— исследовать функции и строить их графики.
Ученик получит возможность:
— выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
— уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
— применять тождественные преобразования для решения задач из различных разделов курса.
Неравенства
Выпускник научится
— понимать терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
— решать линейные неравенства с одной переменной и их системы;
— решать квадратные неравенства с опорой на графические представления;
— применять аппарат неравенств для решения задач из различных разделов курса.
Выпускник получит возможность:
— овладеть разнообразными приёмами доказательства неравенств;
— уверенно применять аппарат неравенств для решения разнообразных математических задач, задач из смежных предметов и практики;
— применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.
Функции
Выпускник научится
— понимать и использовать функциональные понятия, язык (термины, символические обозначения);
— строить графики квадратичных функций;
— исследовать свойства квадратичных функций на основе изучения поведения их графиков;
— понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира;
— применять функциональный язык для описания и исследования зависимостей между физическими величинами;
— понимать и использовать язык последовательностей (термины, символические обозначения);
— применять формулы, связанные с арифметической и геометрической прогрессиями.
Выпускник получит возможность:
— проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера;
— на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
— использовать функциональные представления и свойства функций решения математических задач из различных разделов курса;
— решать комбинированные задачи с применением формул п-го члена и суммы первых n членов арифметической и геометрической прогрессий, применяя при этом аппарат уравнений и неравенств;
— понимать арифметическую и геометрическую прогрессии как функции натурального аргумента;
— связывать арифметическую прогрессию с линейным ростом, геометрическую — с экспоненциальным ростом.
Элементы прикладной математики
Выпускник научится:
— использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин;
— использовать простейшие способы представления и анализа статистических данных;
— находить относительную частоту и вероятность случайного события;
— решать комбинаторные задачи на нахождение числа объектов или комбинаций.
Выпускник получит возможность:
— понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
— понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных;
— приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы;
— приобрести опыт проведения случайных экспериментов, в том числе с помощью компьютерного моделирования, интерпретации их результатов;
— научиться некоторым специальным приёмам решения комбинаторных задач.
История математики
Выпускник научится:
— описывать отдельные выдающиеся результаты, полученные в ходе развития математики как науки;
— знать примеры математических открытий и их авторов, в связи с отечественной и всемирной историей;
— понимать роль математики в развитии России.
Выпускник получит возможность:
— характеризовать вклад выдающихся математиков в развитие математики и иных научных областей;
— понимать роль математики в развитии России.
Методы математики
Выпускник научится:
— выбирать подходящий изученный метод для решения изученных типов математических задач;
— приводить примеры математических закономерностей в окружающей действительности и произведениях искусства.
Выпускник получит возможность:
— используя изученные методы, проводить доказательство, выполнять опровержение;
— выбирать изученные методы и их комбинации для решения математических задач;
— использовать математические знания для описания закономерностей в окружающей действительности и произведениях искусства;
— применять простейшие программные средства и электронно-коммуникационные системы при решении математических задач.




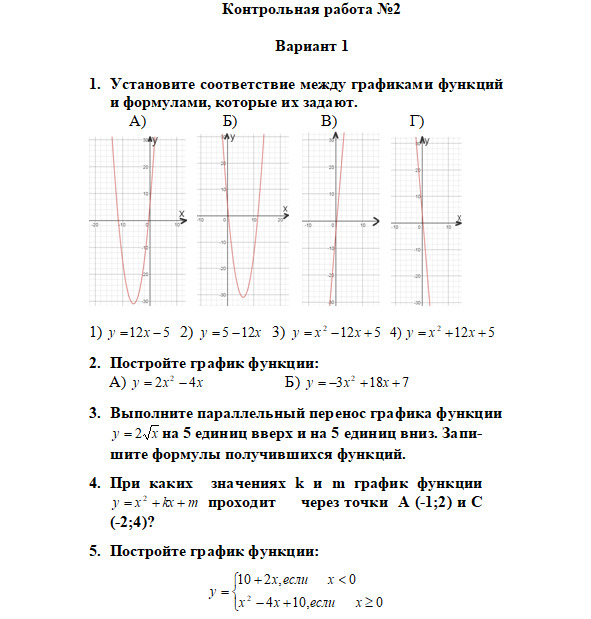
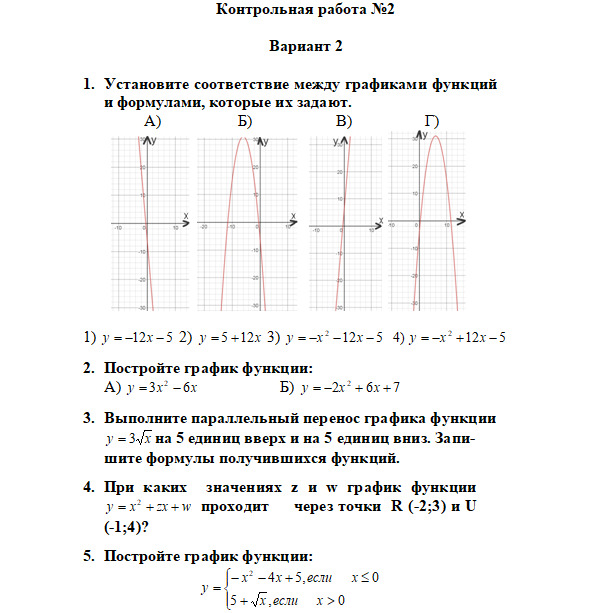
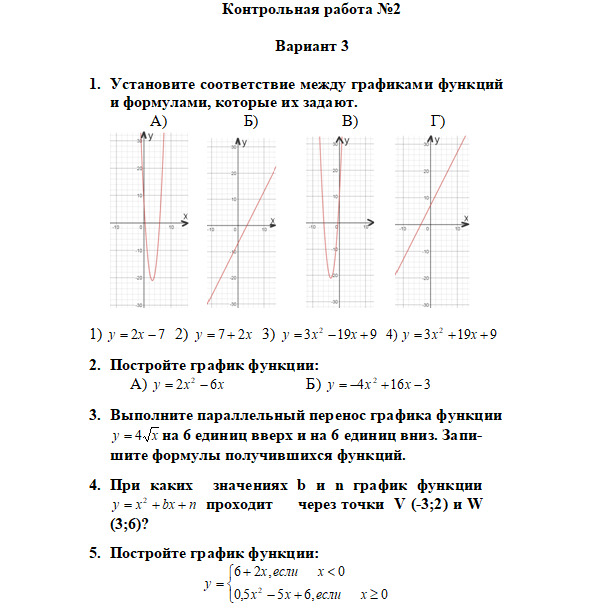
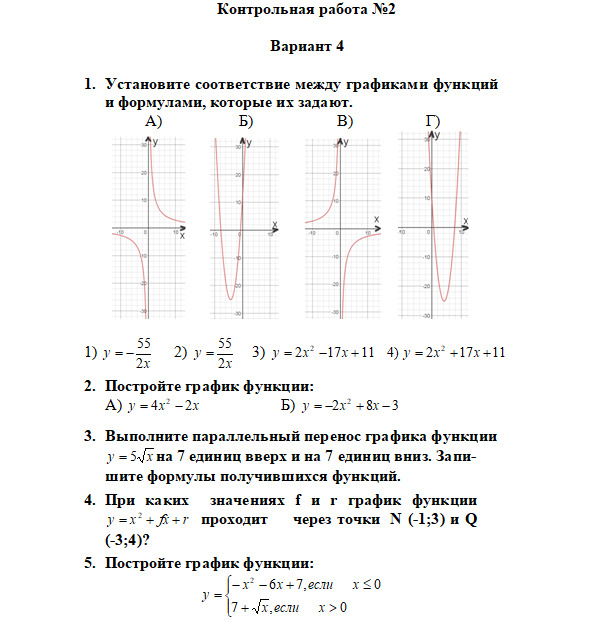






Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.