Бесплатный фрагмент - Квадратные уравнения

Посвящаю своим ученикам школы №15 
г. Перми, в особенности одноклассникам моего сына (Алексею Макарычеву, Максиму Григорцу, Владимиру Печенкину и другим), с которыми общались незабываемые три с половиной года.

Автор

ПРЕДИСЛОВИЕ

Данная книга является самой первой в серии «Школьная математика ОТ и ДО» и первой в теме «Квадратные уравнения».

Предполагается издать четыре части — квадратные уравнения: от определения до применения; от упражнений до олимпиадных задач; от древности до современности; от начальной школы до выпускных классов.

За несколько лет, которые прошли с момента возникновения общей идеи этой серии, эфемерность замысла оформилась в конкретные разработки, к реализации которых были подключены студенты математического факультета Пермского государственного педагогического, а теперь уже гуманитарно-педагогического университета.

Эти книги помогут школьникам в математическом самообразовании (первые три части), учителям — в методическом. Студентам — как в том, так и в другом. Содержание первых трёх частей можно использовать для создания элективных курсов, курсов по выбору и разнообразных форм дополнительного математического образования, а четвёртая позволит построить оптимальную систему обучения математике в школе.

                                   ***

Казалось бы, что может быть банальней в школьном курсе математики, чем квадратные уравнения? Разве что только таблица умножения.

Нередко «оценочным признаком» низкой математической подготовки школьника служит фраза «он даже квадратные уравнения не умеет решать». Предполагается, что этот процесс должен стать инструментом, применяемым «легко и непринуждённо», а не оставаться самостоятельной задачей, требующей значительных затрат умственных ресурсов.

Однако, обидное пренебрежение этим математическим объектом, на наш взгляд, весьма ошибочно. Квадратные уравнения таят в себе удивительно занимательную теорию, полезную для взрослеющего и пытливого ума. Собственно этими соображениями мы и хотим поделиться.

Не надо думать, что все предложенные теоретические факты необходимо запоминать (хотя некоторые стоило бы). Просто из того минимума, содержащегося в школьном курсе математики, при большом желании можно вытянуть закономерности, позволяющие существенно облегчить жизнь решателям математических задач.

Решать квадратные уравнения — что это?

Наука или искусство?

С первого — математического — взгляда, конечно наука!!!

Квадратные уравнения — это математическое понятие, процесс его решения имеет определённый алгоритм, который применяется для решения других (математических, физических, а порой и жизненных) задач.

А искусство, что оно? Только для души!

Но если решать квадратные уравнения не только для дела, но и для души, то вы с высокой вероятностью увидите красоту в этом привычном процессе.

Для изображения картин тоже необходимы техника рисунка, правила перспективы и т. д. Но каждый художник вкладывает в своё произведение собственное видение жизни.

Так и при решении квадратных уравнений можно не ограничиваться известным алгоритмом, а творчески выбирать приёмы получения корней.

В этой — первой — части саги о квадратных уравнениях мы представляем их математическую теорию, а возможность применить её у читателя будет во второй части «Квадратные уравнения от упражнений до олимпиадных задач».

Между прочим, теория — какая бы она ни была — не берётся из ниоткуда. Когда-то и квадратные уравнения были серьёзным объектом для математических исследований. Поэтому третья часть — «Квадратные уравнения от древности до современности» — ждёт своего часа.

Заранее обговорим те ограничения, которых будем придерживаться в рамках данного изложения. Прежде всего, учитывая, что квадратные уравнения начинают изучаться в восьмом классе, мы без специальных комментариев используем все математические знания «предыдущих лет». Там, где на наш взгляд, появляются спорные с точки зрения последовательности изучения факты, мы отсылаем к приложению или сноскам.

Кроме того, в основном тексте книги опущены строгие математические подробности, которые касаются таких понятий как собственно «уравнение» и его видов, дающих представление о «родословной» квадратного уравнения. Если читатель не знает (или забыл) эти факты, он может обратиться к приложению или комментариям.

Автор благодарит своих выпускниц математического факультета Пермского государственного педагогического университета Марию Волкову (2002 г.), Ольгу Крысову (2003 г.) и Инессу Баранову (2008 г.), фрагменты чьих курсовых и выпускных исследований вошли в эту книгу.

Благодарю всех, кому идея создания подобного рода книг созвучна и тех, кто, ознакомившись с книгой, не найдёт её целесообразной.

РАЗДЕЛ I.
ОПРЕДЕЛЕНИЕ, СТРУКТУРА И ЭЛЕМЕНТЫ КВАДРАТНОГО УРАВНЕНИЯ

§1. Мысли с потолка, ведущие к идее,
или Откуда что взялось?

…Забавное число — ноль. На что ни умножь — само же в результате и получается! Прямо загляденье:

0 × 0 = 0 × 1 = 0 × 2 = 0 × 10 = … = 0, т.е. 0 × a = 0 × 0

Однако, интересно, а будет ли выполняться равенство 0 × a = 02, если вместо нуля поставить произвольное число? Например, какое удвоенное число равно своему квадрату, то есть x × 2 = x2? Или утроенное x × 3 = x2?

Поставим задачу в общем виде: найти число, квадрат которого, равен произведению этого числа на конкретное данное число a. Построим модель: xx = ax или x2 = ax.

Так как мы ищем число, отличное от нуля, то, разделив обе части построенного равенства на x, получим, что x = a.

То есть, если удвоенное число равно своему квадрату, то это число 2, а если утроенное, то 3.

Можно этот факт запомнить — вдруг пригодится?..

                                        ***

…Инструктаж судьи на одном из этапов туристической эстафеты:

— Вам необходимо огородить участок прямоугольной формы, площадью 1 ар для стоянки. Дополнительные очки той команде, которая затратит как можно меньше страховочной верёвки. На старт, внимание, начали!

1 ар — это 100 квадратных метров. Участок может иметь размеры 20 × 5 или 25 × 4. Но наша команда знает, что наименьший периметр прямоугольника при его заданной площади будет в том случае, если он — квадрат (теперь и вы это помните!). Отлично! Значит необходимо найти сторону квадрата, если его площадь равна 100. Ну, это легко! Ещё с младших классов, благодаря большой вычислительной практике, помним, что число 10 умноженное на себя даёт сто.

Хорошо, что мы не на уроке математики, а то пришлось бы составлять уравнение x2 = 100…

                                   ***

…Не так давно с нами эксперимент проводили: надо было из множества прямоугольников разнообразной формы выбрать один, который покажется самым приятным на вид. Многочисленные повторения этого опыта показали, что чаще всего люди выбирают те прямоугольники, стороны которого относятся как «золотая пропорция». Золотое (или гармоническое) сечение — это такое деление отрезка, при котором отношение всего отрезка к большей части равно отношению большей части к меньшей 1: x = x: (1 — x).

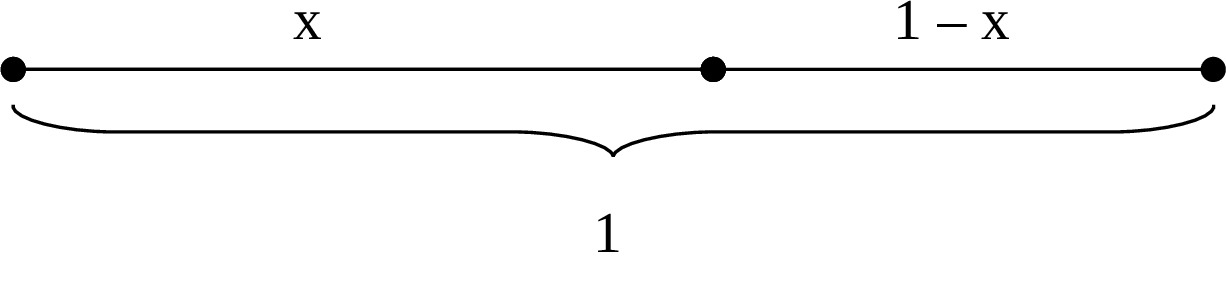
Если воспользоваться свойством пропорции (произведение крайних членов равно произведению средних), то можно получить уравнение, чтобы найти длину большей части этого отрезка: x2 = 1 — x.

                                   ***

…В каком прямоугольном треугольнике стороны выражаются тремя последовательными натуральными числами?

Пусть n длина меньшего катета, тогда второй катет и гипотенуза выражаются как (n +1) и (n +2).

По теореме Пифагора все длины увязываем в уравнение:

                             n2 + (n +1) 2 = (n +2) 2…

                                   ***

Пифагорейцы исследовали фигурные числа, в частности, треугольные (их можно изобразить в виде треугольника).

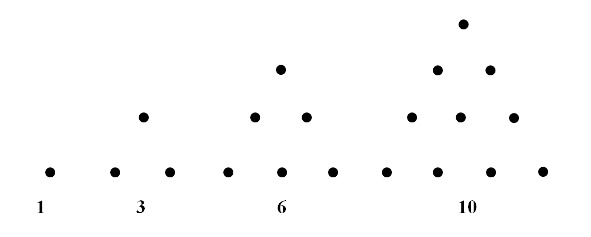
Треугольное число с номером n можно найти как половину произведения n× (n+1). Для ответа на вопрос, является ли треугольным число 45 и если да, то каков его номер, надо решить уравнение n× (n+1) = 90…

                                   ***

Задумайте два натуральных числа от 1 до 20. Найдите их сумму и произведение. Сообщите мне. Я отгадаю задуманные вами числа. Вам интересно, как я это сделаю?..

§2. Кто есть кто,
или Определение квадратного уравнения

Квадратным называется уравнение вида ax2 + bx + c = 0, где a, b, c — некоторые заданные действительные числа, причём a ≠ 0, а x принимается за неизвестное.

Числа a, b, c называют так:

a — старшим или первым коэффициентом,

b — вторым,

c — свободным или третьим.

«Нумерация» коэффициентов зависит не от их реального месторасположения, а от того, при какой степени неизвестной они находятся. Например, число 2 будет первым коэффициентом в любом из трёх уравнений:

5x +2x2 — 7 = 0,

3 — x +2x2 = 0,

2x2 +7x +5 = 0.

А вот число 5 в третьем уравнении является свободным коэффициентом, а в первом уравнении — вторым коэффициентом.

То есть первый (старший) коэффициент — это множитель при квадрате неизвестной, второй — при первой степени. Свободный (третий) коэффициент — это слагаемое без неизвестной, то есть «свободный от неизвестной».

Очевидно, что в качестве неизвестного необязательно брать букву x. Более того, привыкнув за школьные годы к этому неизменному обозначению, среднестатистический ученик начинает испытывать затруднения в восприятии (узнавании, интерпретации) квадратных уравнений, встречающихся при решении более сложных математических (физических и других) задач.

Собственно говоря, и коэффициенты квадратного уравнения не всегда могут обозначаться указанными выше буквами. Одним словом, квадратное уравнение имеет вполне определённую структуру, а как обозначаются элементы этой структуры — дело десятое. Человек со сложившимся математическим стилем мышления понимает, что квадратным уравнением будет являться любое равенство, в правой части которого стоит ноль, а в левой — сумма трёх слагаемых, одно из которых является произвольным числом, другое — произведением произвольного числа на первую степень неизвестного и третье — произведением ненулевого числа на вторую степень неизвестного.

Тогда квадратными будут уравнения:

mx2 + nx + k = 0 (относительно x, m ≠ 0),

xa2 + ya + z = 0 (относительно a, x ≠ 0).

Уравнение y2 + xy + x2 = 0 можно рассматривать как квадратное, но только либо относительно x, либо только относительно y.

Пока же договоримся, что теоретические вопросы будем излагать на привычных обозначениях.

Вернёмся к определению. Давайте выделим внешние, «бросающиеся в глаза», черты квадратного уравнения. Во-первых, наличие знака равенства. Отсутствие его с очевидностью снимает вопрос о правомерности называть объект уравнением.

(Любое ли равенство является уравнением — разговор особый и не в рамках этой книги.)

Во-вторых, левая часть нашего равенства представляет собой алгебраическую сумму трёх слагаемых.

Возникает первый вопрос: обязательно трёх?

Другими словами количество слагаемых — это определяющий признак или нет? Давайте посмотрим.

Значения второго и свободного коэффициентов квадратного уравнения в определении никак не ограничиваются (в отличие от первого). Следовательно, они могут быть равными нулю. Тогда под определение квадратного подходят уравнения вида

ax2 + bx = 0 (c = 0, ab ≠ 0),

ax2 + c = 0 (b = 0, ac ≠ 0),

ax2 = 0 (b = c = 0, a ≠ 0).

Но в левых частях этих уравнениях не три слагаемых!

Тем не менее, это — квадратные уравнения, потому что их можно записать так

ax2 + bx +0 = 0,

ax2 +0 · x + c = 0,

ax2 +0 · x +0 = 0.

Так как количество слагаемых левой части уравнений ax2 + bx = 0, ax2 + c = 0, ax2 = 0 визуально меньше, чем может быть, их называют неполными квадратными уравнениями. Тогда как квадратное уравнение ax2 + bx + c = 0, в котором все коэффициенты отличны от нуля, называют полным.

Таким образом, отсутствие в записи конкретного уравнения свободного члена или слагаемого с первой степенью неизвестного не даёт нам права сомневаться в том, что уравнение всё-таки квадратное. Однако и наличие их не является веской причиной отнести уравнение к квадратным. Об этом чуть ниже.

Следующим возникает вопрос, а почему, собственно a ≠ 0? (Конечно, искушённый читатель знает почему.) Можно ли, например, уравнение вида ax2 + (a — 1) x + a = 0 (или в общем виде f (a) x2 + g (a) x + h (a) = 0) называть квадратным?

Давайте похулиганим и поставим в качестве первого коэффициента ноль. Тогда уравнение примет вид bx + c = 0.

Но это же линейное уравнение! Оно имеет свою теорию, свои изюминки.

Пусть будут «мухи отдельно, котлеты отдельно».

Теперь понятно, что требование a ≠ 0 необходимо для сохранения в квадратном уравнении второй степени — квадрата — неизвестного. Вот этот признак будет определяющим!

В дальнейшем, говоря о квадратном уравнении, мы будем помнить, что старший коэффициент не равен нулю, не оговаривая это каждый раз. Договорились?

Тогда уравнение f (a) x2 + g (a) x + h (a) = 0 правильно называть уравнением с параметром второй степени, которое при определённых условиях может быть квадратным, а может им и не быть (стать линейным).

Однако не будем торопиться. Наличие второй степени неизвестного — необходимый, но не достаточный признак квадратного уравнения.

Рассмотрим следующие уравнения:

ax2 + by + c = 0 и ax2 + bx3 + c = 0.

Выполним сравнительный анализ этих уравнений с квадратным ax2 + bx + c = 0 по трём признакам:

— наличие второй степени неизвестной,

— наибольшая степень неизвестной,

— количество неизвестных.

Зафиксируем для каждого уравнения эти параметры.

Результаты сравнительного анализа организуем в таблицу.

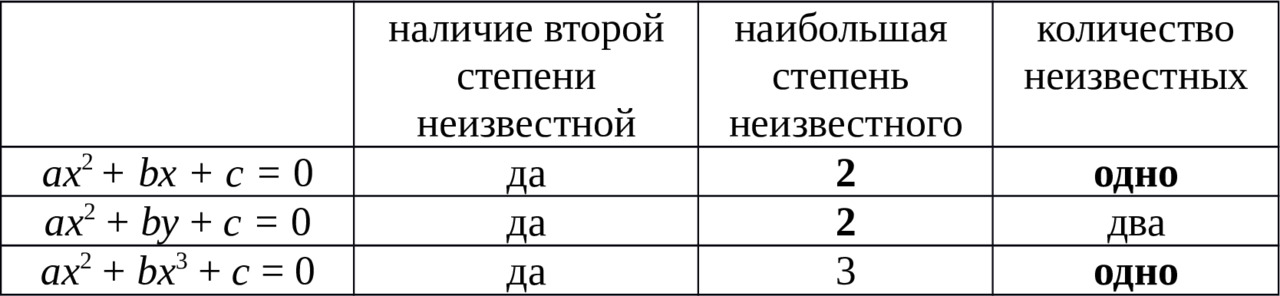
Итак, что мы имеем?

Наличие второй степени неизвестного является общим для всех трёх уравнений. Но по двум другим признакам сравнения, квадратное уравнение отличается: в квадратном уравнении вторая степень неизвестной является наибольшей и неизвестная только одна.

Именно это и важно!

Собственно говоря, квадратным является целое рациональное (или по-другому — алгебраическое) уравнение второй степени с одним неизвестным.

Процесс ограничения класса алгебраических уравнений можно представить в двух направлениях:

алгебраическое уравнение → первой степени, второй степени и так далее;

алгебраическое уравнение → с одной неизвестной, с двумя неизвестными и так далее.

Приведём примеры:

ax + b = 0 — уравнение первой степени с одной неизвестной;

ax + by + c = 0 — уравнение первой степени с двумя неизвестными;

ax2 + bx + c = 0 — уравнение второй степени с одной неизвестной;

ax2 + bxy + cy2 + kx + ly + m = 0 — уравнение второй степени с двумя неизвестными.

Тогда ближайшими родовыми понятиями для квадратного уравнения будут: алгебраическое уравнение второй степени или алгебраическое уравнение с одним неизвестным. Выбирая в качестве родового понятия разные объекты, мы сможем получить различные формулировки определения квадратного уравнения. Попробуйте!

Наконец, рассмотрим правую часть равенства в определении квадратного уравнения. Она представляет собой конкретное число — ноль. А может быть что-нибудь другое?

Если мы хотим видеть квадратное уравнение «в чистом виде», то ничего, кроме нуля, в правой части быть не должно. Но…

Рассмотрим уравнение ax2 + bx + c = m, где m число отличное от нуля. Тогда мы, основываясь на равносильности преобразований уравнений, можем записать

ax2 + bx + c — m = 0

ax2 + bx + (c — m) = 0

ax2 + bx + c1 = 0.

То есть мы, собственно, получили квадратное уравнение.

Ещё пример:

ax2 + bx + c = mx + n

ax2 + bx + c — mx — n = 0

ax2 + bx — mx + c — n = 0

ax2 + (b — m) x + (c — n) = 0

ax2 + b1 x + c1 = 0.

Таким образом, уравнения двух приведённых выше видов
ax2 + bx + c = m и ax2 + bx + c = mx + n есть смысл назвать сводящимися к квадратным. То есть, если в правой части стоит многочлен с одной (той же, что и в левой части!) неизвестной степени не выше первой, то с помощью соответствующих преобразований квадратное уравнение мы получим без проблем.

Если же в правой части будет стоять многочлен с одной неизвестной второй степени, то квадратное уравнение может и не получиться.

Ситуация первая: ax2 + bx + c =ay2 + by + c.

Как бы ни старались, квадратного уравнения мы не получим. Неизвестных две, и это равенство не входит в множество математических объектов «квадратные уравнения». Вывод: неизвестная правой части должна быть такой же, что и в левой!

Ситуация вторая. Преобразуйте самостоятельно, например, два следующих уравнения:

ax2 + bx + c = kx2 + mx + n

ax2 + bx + c = ax2 + mx + n.

Получилось ли у вас квадратное уравнение в первом случае? А во втором? Как будет называться уравнение, которое сведётся не к квадратному?

Определите условие, при котором уравнение такого вида всё-таки будет сводиться к квадратному.

Как ещё один пример рассмотрите уравнение
x2 — 9 = (x — 5) (x +7).

Таким образом, наличие второй степени неизвестной в записи уравнения не всегда будет означать, что оно квадратное.

Очевидно, что если в правой части стоит многочлен с одной переменной степени выше второй, то квадратного уравнения мы ни при каких условиях не получим.

Итак, есть квадратные уравнения, а есть уравнения, сводящиеся к квадратным.

Анализ определения завершён!

§3. Малочисленная семейка,
или Виды квадратных уравнений

В предыдущем параграфе нам пришлось уже упомянуть первую типизацию квадратных уравнений: полные и неполные. В полных квадратных уравнениях ни один из коэффициентов не равен нулю; в неполных — второй и/или третий нулю могут быть равны. Общее представление можно получить из таблицы:

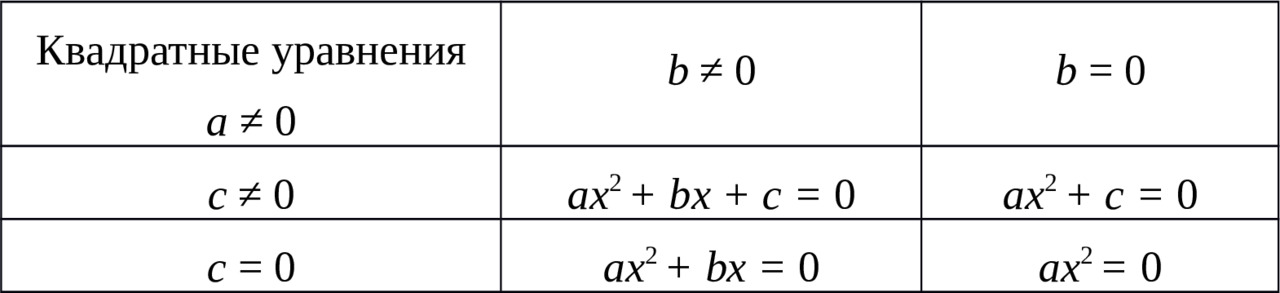
Кроме деления всех квадратных уравнений на полные и неполные для теории, а главное — для практики, в некоторых случаях важно различать два их вида: приведённые и неприведённые. В первом случае старший коэффициент квадратного уравнения равен 1, а во втором — отличен от единицы.

Приведённые квадратные уравнения принято обозначать так: x2+px+q=0.

Из любого неприведённого квадратного уравнения с помощью равносильных преобразований всегда можно получить приведённое: разделим все части уравнения на первый коэффициент. Благо он не равен нулю! Это, конечно, не всегда нужно, но возможно всегда.

Например, из уравнения 4x2+4x‒3=0 всегда можно — при необходимости — получить приведённое x2 + x — 0,75 = 0.

Зачем нужно это разделение? Неполные, приведённые…

Во-первых, неполные можно решать, как говорится, легко и непринуждённо.

Есть мнение, что сначала математики научились решать именно неполные квадратные уравнения. Действительно, это можно сделать без дополнительных усилий или знаний: раскладывай себе на множители и всё!

Мы ещё вернёмся к этому процессу (в §9).

Что касается приведённых, то о них наш замечательный разговор тоже впереди. Не будем торопиться.

Систематизируем нашу окончательную информацию по видам квадратных уравнений:

Вся совокупность квадратных уравнений — полных и неполных, приведённых и неприведённых, с целочисленными, дробными, рациональными или иррациональными коэффициентами — составляет так называемый объём школьно-математического понятия «Квадратное уравнение».

В школьной математике есть традиция преобразовывать данное квадратное уравнение с рациональными коэффициентами таким образом, что бы все его коэффициенты были целыми числами, а старший коэффициент положительным. Например,

— 0,3x2 +0,03x +1 = 0  →  30x2 — 3x — 100 = 0.

Это совершенно не обязательно, хотя, безусловно, в большинстве случаев облегчает процесс решения. А вот для теоретических исследований эти условия — целочисленность коэффициентов и положительность первого — удобны. Это позволяет с большей определённостью делать выводы.

Кроме того, в третьем разделе нам понадобится одно определение, которое не является «общепризнанным», но мы его сформулируем сами.

Будем считать, что квадратное уравнение с целочисленными коэффициентами имеет канонический вид, если наибольший общий делитель всех его трёх коэффициентов равен 1.

Это определение нам необходимо для того, чтобы не было возможности поделить все слагаемые левой части уравнения на какое-нибудь одно и то же целое число.

§4. Квадратные уравнения и Ко

Иногда школьники, не открывшие для себя необходимость в математических знаниях, небрежно называют квадратными уравнениями объекты, хоть и имеющие с ними непосредственную связь, но таковыми не являющиеся.

Рассмотрим некоторые, визуально схожие, конструкции и сравним их по следующим признакам:

— внешний вид,

— наличие знака отношения,

— количество неизвестных.

По традиции результат анализа оформим в таблицу и добавим соответствующие каждой математической конструкции термины. Знакомьтесь (или просто внимательно смотрите).

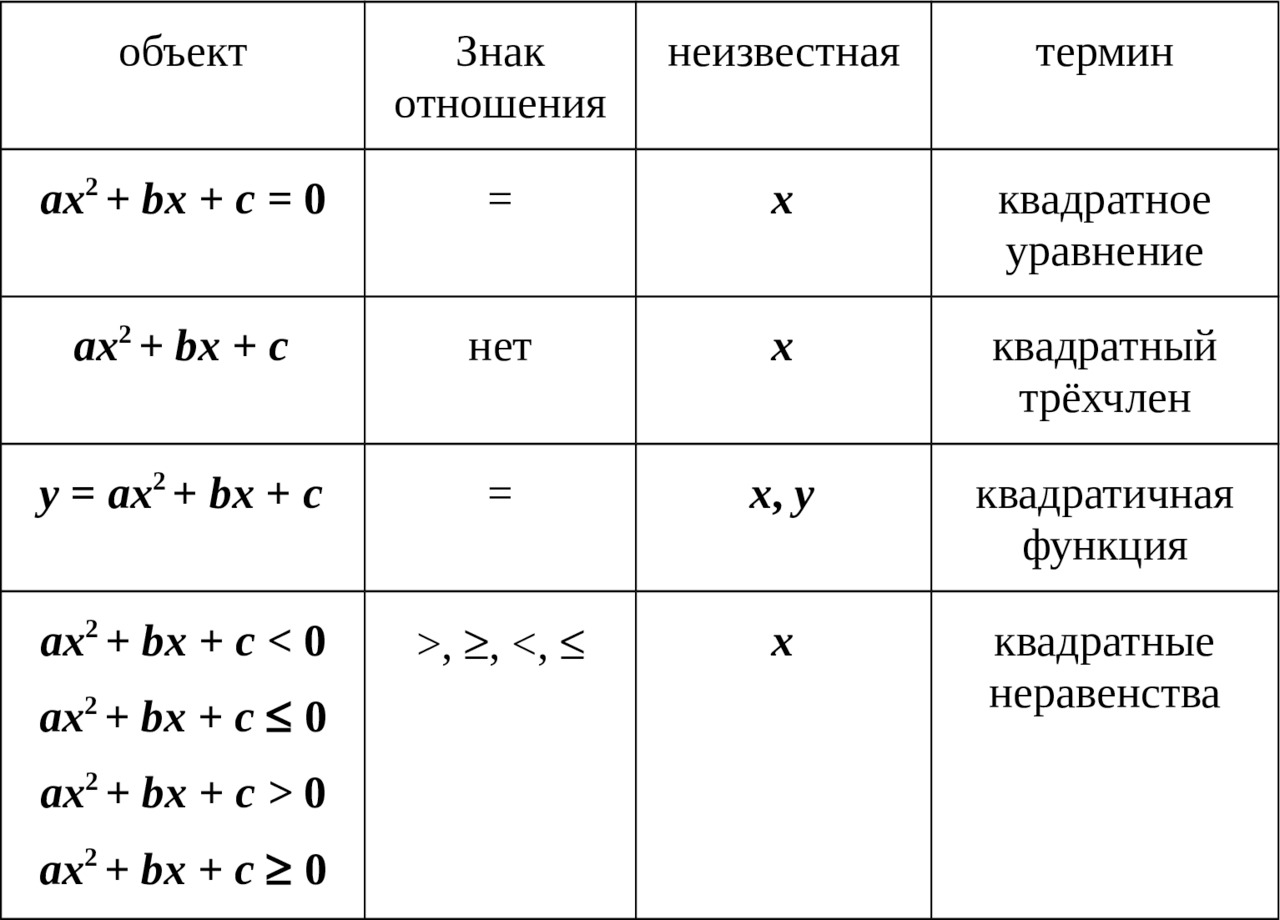
Таким образом, внешне квадратное уравнение отличается от

— квадратного трёхчлена наличием знака отношения, а именно знаком равенства;

— квадратичной функции наличием только одной неизвестной, а не двух переменных величин;

— квадратных неравенств наличием знака отношения, а именно знаком неравенства.

А по сути мы имеем дело с четырьмя абсолютно разными математическими объектами, каждое из которых имеет своё родовое понятие. Но, безусловно, все четыре тесно взаимодействуют друг с другом.

За «первооснову» можно взять квадратный трёхчлен, то есть выражение вида ах2 + bх + с, где а, b, с — заданные числа, причём a ≠ 0 и х — переменная величина.

При рассмотрении различных аспектов квадратного трёхчлена возникают новые математические модели.

Если каждому значению переменной поставить в соответствие значение самого квадратного трёхчлена, то получаем квадратичную функцию y = ax2 + bx + c.

При нахождении корней квадратного трёхчлена — квадратное уравнение ax2 + bx + c = 0.

Выяснение знакопостоянства значений квадратного трёхчлена приводит к построению квадратных неравенств.

С каждым из этих математических объектов производятся только определённые манипуляции:

— квадратные уравнения и неравенства можно (и, конечно, нужно!) решать, но нельзя раскладывать на множители (это не корректное требование к этим объектам);

— квадратичную функцию исследуют, но не решают;

— квадратный трёхчлен раскладывают на множители или у него выделяют полный квадрат (чего не делают с уравнением или функцией, так как это просто не имеет математического смысла).

Квадратное уравнение можно рассматривать как модель, которая получается при нахождении корней квадратного трёхчлена или нулей квадратичной функции. Кроме того, нахождение корней квадратного уравнения необходимый шаг в решении квадратных неравенств.

Но об этих, не менее замечательных, математических понятиях, мы поговорим в других книгах.

В связи с тем, что в зону нашего внимания попал квадратный трёхчлен, можно сформулировать ещё парочку определений квадратного уравнения:

алгебраическое уравнение вида P (x) = 0 будет называться квадратным, если P (x) — квадратный трёхчлен;

уравнение, в левой части которого стоит квадратный трёхчлен, а в правой — ноль, называется квадратным.

§5. Всегда ищи первопричину!
или Как решить квадратное уравнение?

Всё начинается просто и безоблачно, это потом возникают объективные и надуманные проблемы. Вот и мы пойдём от самого простого к чуть более сложному, но всё равно простому.

Прежде всего, нам надо вспомнить, что такое корень уравнения?

Корнем уравнения называется всякое значение неизвестной, при котором равенство становится истинным. То есть, корнем квадратного уравнения ax2+bx+c=0 будет такое число x, которое при подстановке в левую часть даст нам значение квадратного трёхчлена ax2 + bx + c равное нулю.

Решить квадратное уравнение — это значит найти все его корни или установить, что корней нет.

В связи с этим возникает два вопроса:

— сколько корней имеет квадратное уравнение (то есть до каких пор их искать),

— каким образом их находить (или доказывать, что их нет)?

А вот для этого нам надо знать, что такое квадратный корень из числа. Приступим.

Квадратным корнем из числа называется число, квадрат которого равен данному числу. Из этого определения непосредственно следует, во-первых, что на множестве действительных чисел квадратные корни можно извлекать только из неотрицательных чисел, во-вторых, из положительного числа существует два квадратных корня.

То есть нахождение квадратных корней числа m может дать нам три варианта результата:

— если число m положительное, то квадратных корней два,

— если число m равно нулю, то и квадратный корень из нуля один (сам же ноль),

— если число m отрицательное, то действительных квадратных корней мы не получим.

Тогда при решении уравнения вида t2 = m (по сути это нахождение квадратных корней из числа m), можем получить три варианта ответа (смотри далее в таблице):

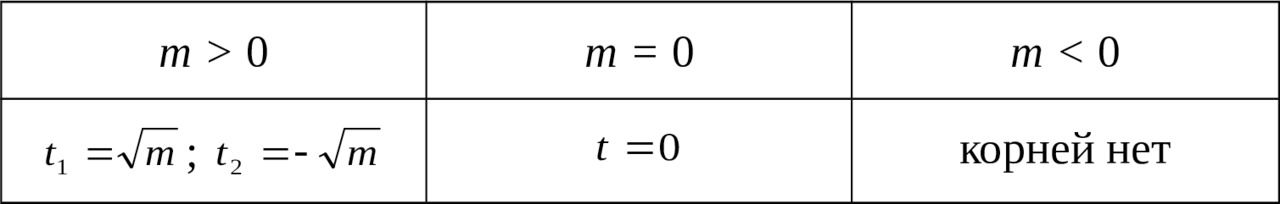
То есть, уравнение t2 = m имеет или два противоположных корня, или единственный, равный нулю, либо не имеет корней.

В качестве числа t можно взять линейный двучлен kx + n
(k ≠ 0). Тогда для m> 0 корни уравнения (kx + n) 2 = m будут равны соответственно:

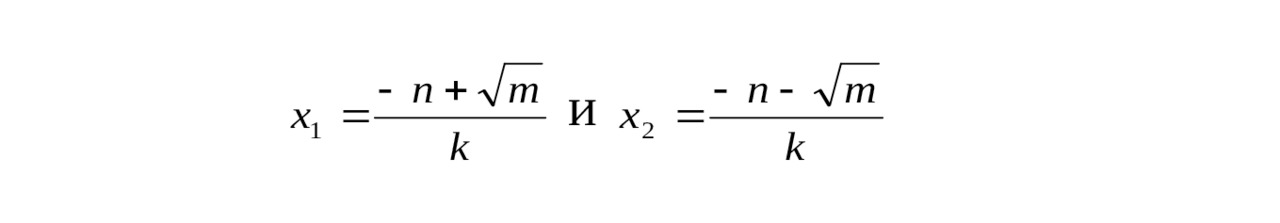
С другой стороны, уравнение (kx + n) 2 = m после нескольких равносильных преобразований будет выглядеть так: k2x2 +2knx + n2 — m = 0 (тоже проверьте!).

То есть оно является квадратным!

А можно ли из квадратного уравнения ax2 + bx + c = 0 получить что-нибудь похожее на (kx + n) 2 = m?

Оказывается, можно.

Этот процесс называется выделением полного квадрата.

Напомним классический его вариант.

Рассмотрим квадратное уравнение ax2 + bx + c = 0.

Сначала разделим обе части уравнения на a (по определению a ≠ 0); это преобразование сохраняет равносильность уравнений, то есть, корни не изменятся. Получаем

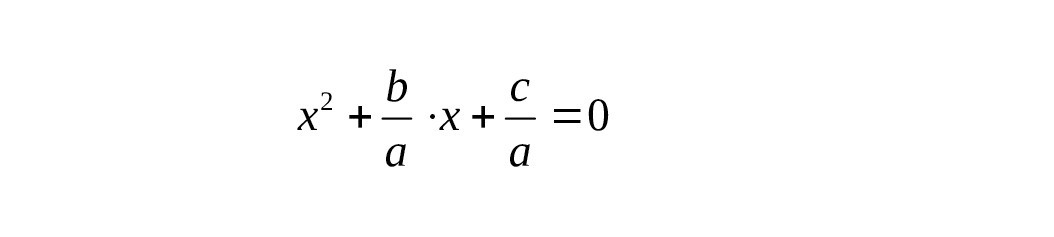
Далее преобразования идут в такой последовательности:

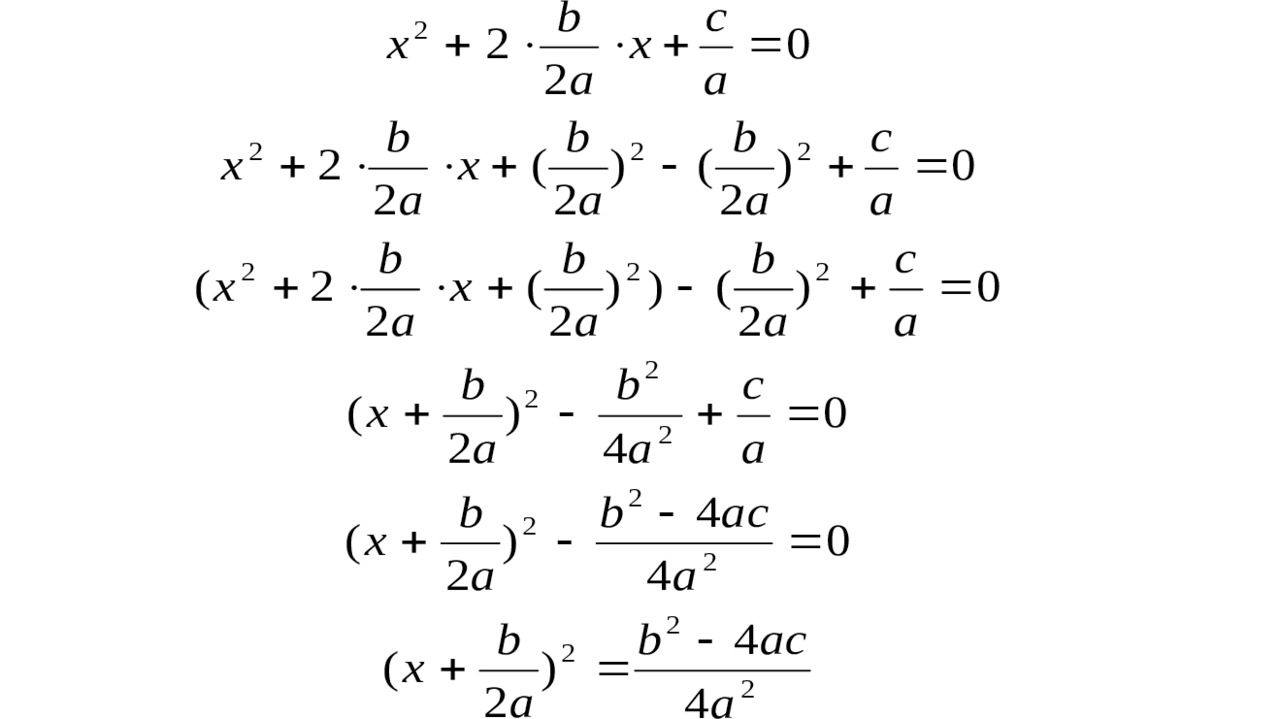
Обозначим выражение (b2 — 4ac) через D.

Тогда полученное равенство примет вид

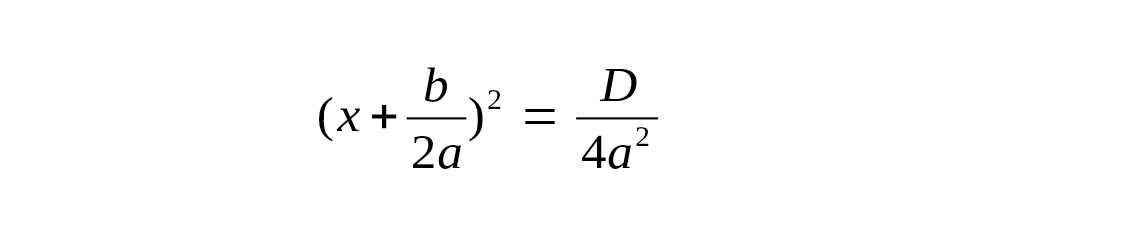
Знак правой части зависит от числителя, так как знаменатель может быть только положительным (обоснуйте — почему?). Тогда возможны три случая.

Как видим, знак числа D определяет наличие и количество корней квадратного уравнения. Поэтому его назвали дискриминантом (от лат. discriminans, род. падеж discriminantis — разделяющий, различающий) квадратного уравнения.

Кстати, выделить полный квадрат в левой части квадратного уравнения можно ещё одним способом.

Он не столь очевиден, но существенно легче.

Смотрите:

ax2 + bx + c = 0

4a2x2 +4abx +4ac = 0

4a2x2 +2 · 2ax · b + b2 — b2 +4ac = 0

(2ax + b) 2 = b2 — 4ac

Далее всё очевидно: выражаем сначала 2ax + b, потом x.

§6. Важный математический аспект,
или Количество…

Вернёмся к общим формулам, но посмотрим на них с других позиций. Не с точки зрения чему могут быть равны корни квадратного уравнения. Сейчас нас будет интересовать количественный аспект.

Итак, мы имеем алгоритм:

1 шаг — вычисляем дискриминант;

2 шаг — делаем вывод о наличии корней;

3 шаг — вычисляем корни по формулам.

Две ситуации, когда дискриминант имеет определённый знак, трактуются вполне однозначно:

если дискриминант отрицательный, то квадратное уравнение корней не имеет;

если дискриминант положительный, то можно найти два различных корня квадратного уравнения.

Кстати, а может ли квадратное уравнение иметь более двух различных корней?

Давайте разберём случай с нулевым дискриминантом.

С одной стороны мы выяснили, что при D = 0 квадратное уравнение имеет один корень (из смысла квадратного корня из нуля)

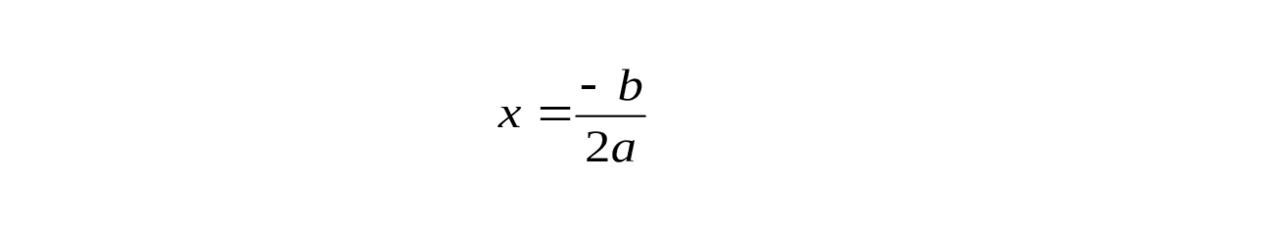
Но если в общих формулах положить D = 0, то получим, что квадратное уравнение имеет два равных корня:

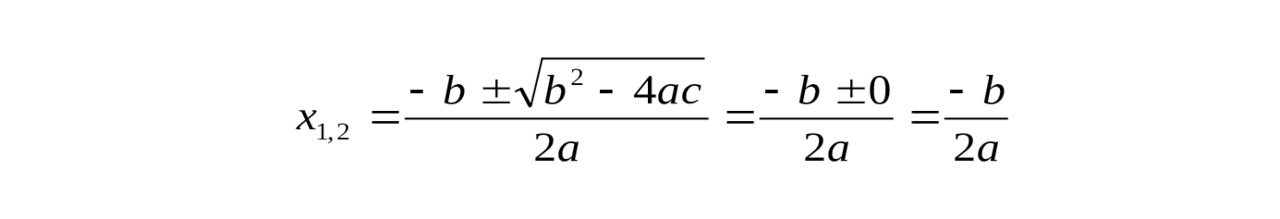
Так как же всё-таки: один корень или два равных?!

С точки зрения высшей алгебры (теории уравнений), то правильной надо признать трактовку «два равных корня», так как количество корней целого рационального уравнения совпадает со степенью этого уравнения. Поскольку квадратное уравнение имеет вторую степень, то и корней у него должно быть два. Но тогда как быть с тем, что при отрицательном дискриминанте корней вроде бы нет?

Оставим на время высшую математику и вернёмся к элементарной. С точки зрения последней оба варианта — «единственный корень» и «два равных корня» — признаются законными.

Существенное значение количество корней приобретает при решении специфических задач, как правило, с параметрами. Двоякое толкование ситуации при D = 0 привносит в математическую жизнь неординарность и бодрость, так как требует внимания и логики.

Для неполных квадратных уравнений всё ещё проще.

1. Уравнение вида ax2 = 0.

Так как первый коэффициент не равен нулю по определению, то равенство может быть истинным только при x = 0 и ни при каких других условиях. В этом случае мы также имеем два равных корня, так как всегда можем записать x · x = 0, то есть оба множителя равны нулю.

2. Уравнение вида ax2 + bx = 0 (b ≠ 0) всегда имеет два различных корня, один из которых всегда равен нулю, а другой отличен от нуля.

Действительно,

       ax2 + bx = 0

     x (ax + b) = 0

       x = 0   или   ax + b = 0.

3. Уравнение ax2 + с = 0 может иметь действительные корни (и тогда они будут либо рациональными противоположными, либо иррациональными сопряжёнными числами), а может и не иметь таковых. Например, уравнение 4x2 — 9 = 0 имеет корни ±1,5; уравнение x2 — 5 = 0 имеет корни плюс-минус квадратный корень из пяти; уравнение 7x2 +5 = 0 действительных корней не имеет.

Для того, чтобы такое неполное квадратное уравнение имело корни необходимо и достаточно, чтобы первый и третий коэффициенты были разного знака.

Докажите этот факт самостоятельно.

§7. …и качество, или Теорема Виета

По праву достойна в стихах быть воспета

О свойствах корней теорема Виета.

Что лучше, скажи, постоянства такого,

Умножишь ты корни — и дробь уж готова:

В числителе с, в знаменателе а.

А сумма корней тоже дроби равна.

Хоть с минусом дробь эта, что за беда —

В числителе b, в знаменателе а.

В. Литцман

Как видно из процесса вывода корней квадратного уравнения наличие последних зависит от знака дискриминанта, значение которого в свою очередь зависит от значений коэффициентов конкретного квадратного уравнения. Да и значение корней, конечно, зависит от этих коэффициентов.

Достаточно посмотреть на формулы

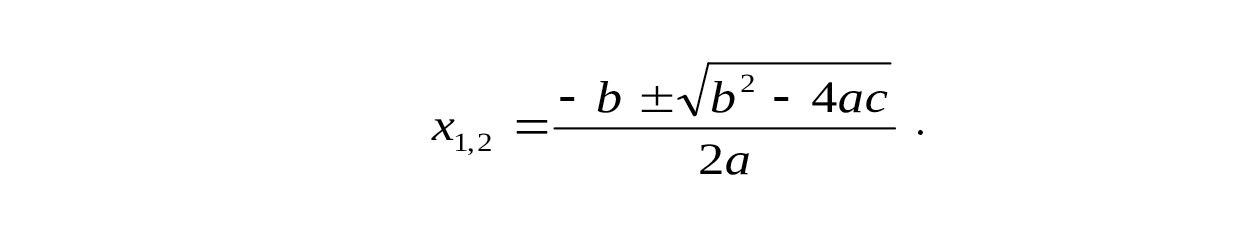
Однако между корнями и коэффициентами квадратного уравнения существует и другая, не столь очевидная связь!

Обнаружил её французский математик Франсуа Виет (1540‒1603) для коэффициентов и корней алгебраических уравнений до пятой степени включительно. «Школьная» теорема Виета является лишь частным случаем классической формулировки.

Напомним школьную формулировку теоремы Виета.

Если квадратное уравнение ax2 + bx + c = 0 имеет корни, то их сумма равна минус второму коэффициенту, делённому на первый, а произведение равно третьему коэффициенту, делённому на первый.

Доказательство этого утверждения достаточно лёгкое. Действительно, если корни уравнения существуют, то их можно выразить известным образом (см. выше известные всем формулы). Далее достаточно сложить и умножить два выражения, чтобы получить необходимые равенства. Сделайте это самостоятельно.

Обратим внимание на то, что УСЛОВИЕМ теоремы является существование корней уравнения, а вот справедливость равенств, связывающих коэффициенты и корни, — это ЗАКЛЮЧЕНИЕ теоремы, то есть факт, который требует доказательства.

К условию и заключению теоремы Виета мы ещё вернёмся. А пока опять о количестве корней квадратного уравнения.

Если мы решили, что при D = 0 корень один, то как может выполняться теорема Виета? Ведь и слагаемых, и множителей должно быть два! Всё-таки — два равных.

Хороший компромисс — введение термина «корень кратности два». То есть корень вроде бы и один, но его кратность (встречаемость) говорит о том, что в конкретных ситуациях учитывать его надо дважды.

С функционально-графической точки зрения удобна ситуация «один корень». Она соответствует тому, что парабола (график квадратичной функции, заданной одним и тем же квадратным трёхчленом что и конкретное квадратное уравнение) имеет с осью абсцисс одну общую точку.

А с позиции разложения на множители квадратного трёхчлена целесообразно говорить о двух равных корнях, так как для одного корня и линейный множитель должен быть один, а у нас их два — уравнение то второй степени!

Вот такой казус: и «один корень», и «два равных» — оба правомерны и необходимы в своих уникальных ситуациях.

В случае отрицательного дискриминанта всё значительно проще: действительных корней у квадратного уравнения нет, на множители квадратный трёхчлен не раскладывается, парабола общих точек с осью абсцисс не имеет. Ну и, конечно, раз условие теоремы Виета не выполняется (помните? «… если корни существуют…»), то и говорить о связи с коэффициентами несуществующих корней, смысла нет.

РАЗДЕЛ II.
МЕТОД, СПОСОБЫ И ПРИЁМЫ РЕШЕНИЯ
КВАДРАТНЫХ УРАВНЕНИЙ

§8. От добра добра не ищут?
или Основной метод решения квадратного уравнения

Если вспомнить, как мы искали возможность вычислить корни квадратного уравнения, то надо признать, что выделение полного квадрата можно считать основным методом решения квадратных уравнений.

А вот использование знаменитых формул уже вторично. Однако их применение значительно облегчает процесс решения.

Допустим, нам необходимо решить уравнение x2 +6x +5 = 0. Выделим полный квадрат левой части:

x2 +6x +5 = x2 +2 ∙ 3 ∙ x +32 — 32 +5 =

= (x +3) 2 — 9 +5 = (x +3) 2 — 4.

Тогда

     (x +3) 2 — 4 = 0

            (x +3) 2 = 4

        x +3 = 2 или x +3 = –2

           x = –1 или x = –5.

Преобразования выполняются легко и непринуждённо.

С уравнением x2 — 8x — 9 = 0, надо думать, тоже особых хлопот не возникнет (попробуйте самостоятельно произвести выкладки).

Давайте рассмотрим уравнение x2 — 7x +6 = 0.

Преобразуем левую часть:

x2 — 7x +6 = x2 — 2 ∙ 3,5 ∙ x +3,52 — 3,52 +6 =

= (x — 3,5) 2 — 12,25 +6 = (x — 3,5) 2 — 6,25

Далее аналогично первому примеру.

Вроде бы не трудно. Но начинает вызывать дискомфорт нечётность второго коэффициента.

Этот дискомфорт уже усиливается при выделении полного квадрата левой части, например, такого уравнения

                    3x2 +5x—8 = 0.

Необходимо сначала поделить обе части уравнения на три, а потом дробное число пять третьих представить как удвоенное произведение… бр-р-р!..

Вообще, чем «интереснее» корни, тем сложнее выделение полного квадрата. А простые корни можно и без него найти. Об этом наш весь дальнейший разговор собственно.

Можно, конечно, привлечь второй вариант преобразований, он чуть легче:

3x2 +5x—8 = 0 (× 12)

36x2 +60x—96 = 0

36x2 +2 · 6x · 5 +25 — 25 — 96 = 0

      (6x +5) 2 = 121

6x +5 = 11 или 6x +5 = ‒11

Далее решаем простые линейный уравнения.

Словом, выделением полного квадрата решать квадратные уравнения можно, но не оправдано сложно. Значимость его, однако, в том, что с его помощью можно получить формулы, а значит существенно облегчить процедуру нахождения корней квадратного уравнения.

С помощью формул можно решить любое (!) квадратное уравнение.

Кроме того, находя дискриминант, быстро становится понятным, имеет уравнение корни или нет (по знаку дискриминанта).

Кстати сказать, с понятием дискриминанта связаны первые признаки и свойства существования (и не существования) корней квадратного уравнения.

Для того, чтобы квадратное уравнение имело два различных корня, необходимо и достаточно, чтобы его дискриминант был положительным.

Для того, чтобы квадратное уравнение имело два равных корня (единственные корень), необходимо и достаточно, чтобы его дискриминант был равен нулю.

Для того, чтобы квадратное уравнение не имело корней (действительных, разумеется), необходимо и достаточно, чтобы его дискриминант был отрицательным.

И, конечно же, формулы незаменимы, если оба корня квадратного уравнения — иррациональные числа.

Одним словом, использование формул является универсальным и самым распространенным способом решения квадратных уравнений.

В принципе, тем, для кого квадратные уравнения не представляют интереса или нужны только в утилитарных целях, этих формул вполне достаточно. Дальнейший разговор для тех, кто разделяет нашу точку зрения: решать квадратные уравнения — это искусство!

§9. Стандартные отступления от «стандарта»

Отдельный разговор о неполных квадратных уравнениях.

При их решении вообще необязательно применять знаменитые формулы. Но ничто и не мешает их применять! Вопрос встаёт только о целесообразности. Но попробуйте самостоятельно получить формулы корней неполных квадратных уравнений в общем виде (см. таблицу) с помощью формул универсальных.

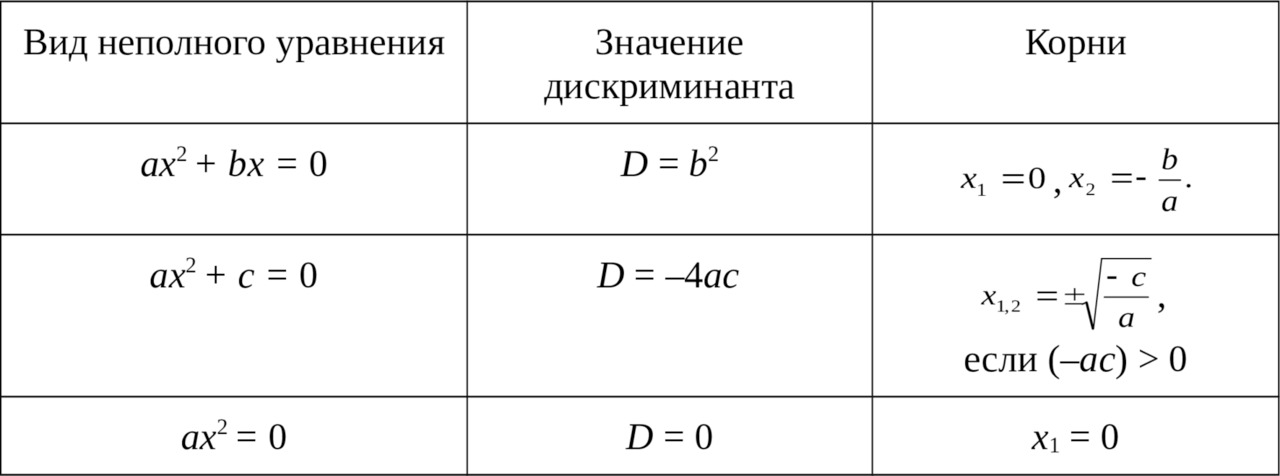
С полными квадратными уравнениями всё сложнее и интереснее!

Для начала рассмотрим квадратное уравнение, у которого второй коэффициент является чётным: ах2 +2тх + с = 0.

Пусть данное уравнение имеет корни. По общей формуле корней квадратного уравнения получаем:

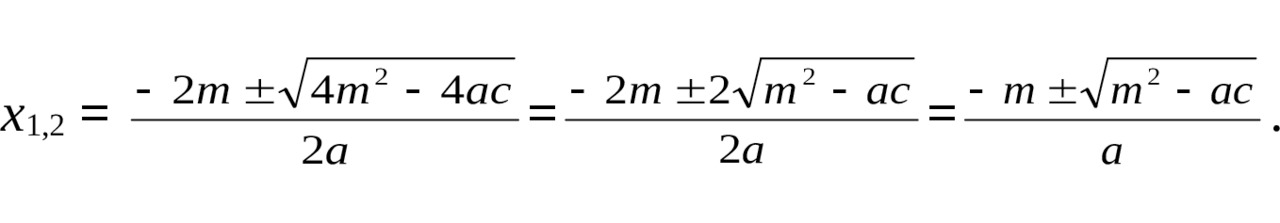
Преобразуем m2 — ac:

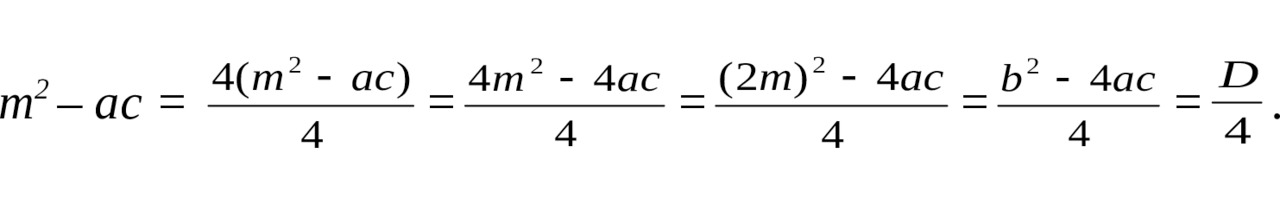
Следовательно, для решения квадратного уравнения с чётным вторым коэффициентом можно применять модифицированные формулы: сначала считаем дискриминант, делённый на четыре, затем вычисляем корни по формулам

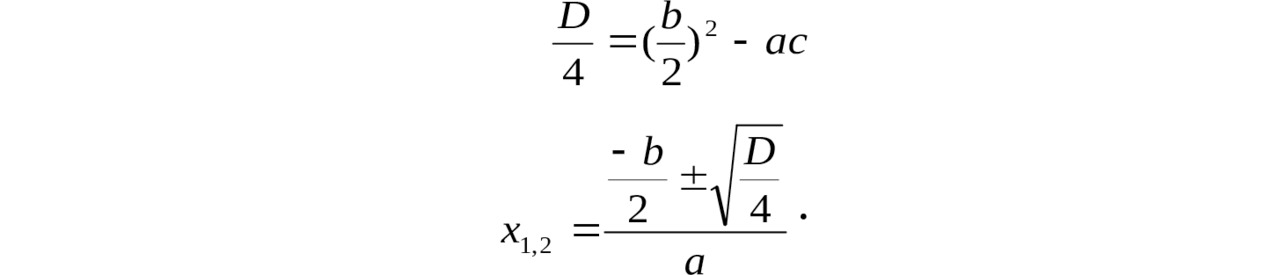
Ещё один вариант вывода этих же модифицированных формул для квадратного уравнения с чётным вторым коэффициентом:

ах2 +2тх + с = 0  (D = 4m2 — 4ac).

Разделим обе части уравнения на 2:

(a/2) x2 + mx + (c/2) = 0

D1 = m2 ‒ac = (D/4)

Далее по классическим формулам корней.

Для чего нужны эти другие формулы?

Конечно же, для простоты вычислений.

Справедливости ради скажем, что применять новые формулы не всегда целесообразно. Не для каждого такого квадратного уравнения они действительно облегчают нахождение корней.

Например, если b = 110, то само это число проще возвести в квадрат, чем его половину 55: 112 → 121 → 12100.

В случае b = 60 или b = 324 действия возведения в квадрат самого числа и его половины фактически «равнозатратны» (одинаково легко или одинаково трудоёмко).

Но, например, при b = 28, очевидно, что проще возвести в квадрат 14.

Однако каждый сам для себя решает степень удовольствия и удовлетворения от применения этих формул.

Единственно, что ещё надо заметить, что формулы чётного второго коэффициента позволяют сразу получать преобразованные иррациональные корни.

Сравните:

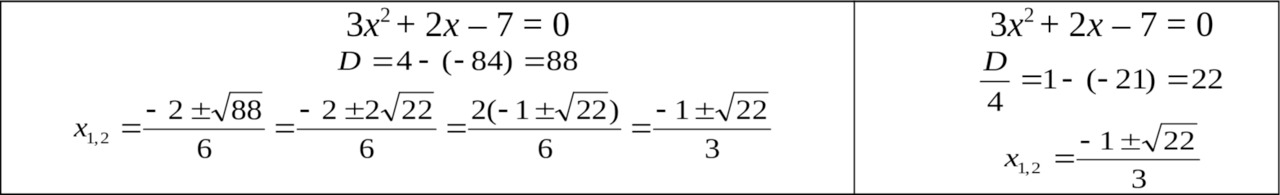
В методической и учебной литературе двадцатого века я обнаружила ещё и формулы для приведённого квадратного уравнения x2 + px + q = 0. Признаться, не понимаю, для чего нужны формулы общего вида для приведённых квадратных уравнений, но один вариант меня всё же приятно удивил. Если приведённое квадратное уравнение имеет чётный второй коэффициент, то эта формула восхитительна:

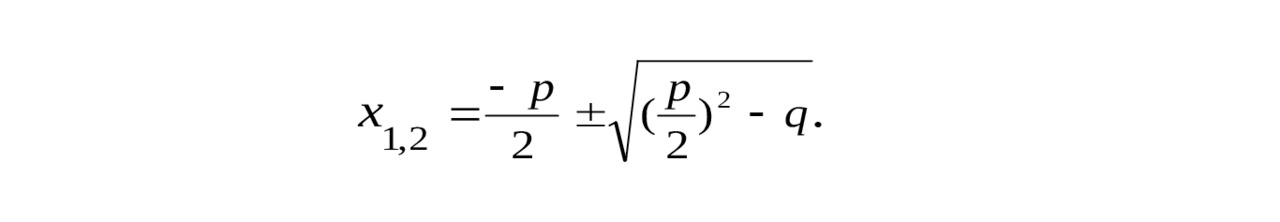
Как по мне, так очень изящно!

§10. Любимый способ нахождения корней с неправильным названием,
или Метод подбора

Очень часто школьники любят находить корни приведённого квадратного уравнения с целочисленными коэффициентами «по теореме Виета». Популярность этого способа весьма радует, а вот название вызывает веские возражения.

С помощью теоремы Виета можно решать много всяких задач, но вот как раз решать квадратные уравнения «по ней» мы не можем.

Если математически грамотно вчитаться в условие школьной теоремы Виета, то внимание цепляет условие «если квадратное уравнение имеет корни…». Если имеет! А ведь мы, начиная решать конкретное квадратное уравнение, не всегда можем со стопроцентной уверенностью сказать, что корни существуют. Как же мы можем применять теорему?

То, что школьники (и, к большому сожалению, некоторые учителя!) называют «по теореме Виета», на самом деле называется способом подбора с дальнейшей проверкой теоремой обратной теореме Виета. Помните?