
Бесплатный фрагмент - Комбинаторика путевого развития горочных горловин
Аннотация
В книге авторы предложили метод расчета всех возможных вариантов схем сортировочных устройств различных мощностей. Расчет производился для сортировочных горок малой мощности, которые имеют ограничение до 16 путей в сортировочном парке. Он основывался на методе триангуляций выпуклых многоугольников, где каждый треугольник представляет собой разделительный элемент (стрелочный перевод), а ребра многоугольника (за исключением нижнего) — пути сортировочного парка. Вычисление графов-деревьев горочных горловин производилось на основе критерия, который накладывают Правила и нормы проектирования сортировочных устройств на железных дорогах колеи 1520 мм: разница между числом путей в двух частях горочной горловины не должна превышать единицы. На основании предложенного метода расчета авторы в Приложении впервые в проектировочной науке привели все возможные схемы сортировочных горок малой мощности (138 схем). В работе проведен анализ этих схем методом кластеризации (-средних) с целью выявления вариантов с наименьшей длиной, которая обеспечивает рациональные параметры сортировочных горок: конструктивную высоту, величину и длину скоростных уклонов и мощность тормозных средств, необходимую для регулирования скорости скатывания отцепов. В заключении авторы дают предложения проектировщикам при выборе схем проектирования или реконструкции путевого развития сортировочных устройств.
Светлой памяти профессора МИИТа
Шубко Владимира Григорьевича посвящается
Вступление
19 марта 2019 года правительство Российской Федерации утвердило долгосрочную программу развития ОАО «Российские железные дороги» до 2025 года, в которой предусмотрело переход на «цифровую железную дорогу» с целью обеспечения устойчивой конкурентоспособности компании на основе повышения привлекательности транспортных и логистических услуг. Эти услуги будут предоставляться клиентам за счет применения современных цифровых технологий.
В связи с этим особую актуальность приобрела разработка интеллектуально-программных комплексов «цифровой железнодорожной станции», связанных с техническими средствами и устройствами, обеспечивающими расчет и выполнение технологических операций обработки вагонов и поездов на станции и путях необщего пользования с минимальным участием человека.
По информации [6] с 2019 по 2025 год специалисты НИИАС внедрят ряд программно-аппаратных комплексов на 26 сортировочных станциях ОАО «РЖД». «Проект позволит автоматизировать сортировочные работы, сократить время на их проведение, повысить безопасность и даст существенный экономический эффект в масштабах всей сети». По мнению начальника отдела Ростовского филиала АО «НИИАС» Ольгейзера И. А. создание цифровых двойников горочных сортировочных устройств позволит «быстро смоделировать развитие событий в зависимости от тех или иных факторов, определить потенциальные риски, найти наиболее эффективные режимы работы, выстроить шаги по обеспечению безопасности» [3].
Цифровой двойник предполагается создавать из принципов изоморфизма теории множеств, включающего копию технико-технологических элементов сортировочной горки с помощью информации со всех доступных устройств и датчиков. Пусть O — множество состояний сортировочной горки, а W — множество состояний ее цифрового двойника. Под изоморфизмом понимается взаимно-однозначное отображение элементов одного множества в элементы другого множества. Подобная биекция предполагает совпадение количества элементов этих двух множеств, то есть их равномощность. Графически это представлено на рисунке 1.
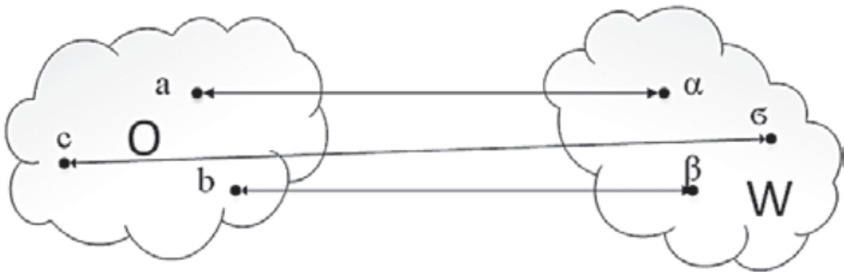
сортировочной горки и ее цифрового двойника
Проблемы цифровизации зарубежных сортировочных горок
Российские проектировщики решают проблемы цифровизации и интеллектуализации процессов роспуска составов на сортировочных горках с 2001 года. Начальник отделения автоматизации и механизации станционных процессов ОАО «НИИАС» Савицкий А. Г. представил оценку состояния этих проблем на зарубежных сортировочных горках в работе [5]. Специалисты ОАО «НИИАС» занимаются проблемами автоматизации и механизации сортировочных процессов уже более двадцати лет. Они пришли к выводу, что уровень сложности задачи управления сортировочным процессом слишком высок и превышает возможности диспетчера. Поэтому проектировщики разработали электронный помощник, реагирующий на «возникающие непростые ситуации на сортировочных станциях» [2].
Российские ученые внимательно следят за развитием цифровых и интеллектуальных систем роспуска составов на зарубежных сортировочных горках. ОАО «НИИАС» накопил огромный опыт, исследуя горки США, Канады, Германии, Индии, Чехии, Словакии и других стран. Например, горочные сортировочные устройства Германии характеризуются высокой степенью автоматизации, низким уровнем повреждений отцепов и грузов при роспуске, а также организационным и технологическим порядком.
При создании интеллектуальных систем оперативного управления сортировочным процессом остается ряд направлений, где цифровизация может использоваться не для всех процессов. Например, процесс проектирования и реконструкции горочных горловин предусматривает использование цифровых программных продуктов лишь для оценки вариантов продольного профиля спускной части сортировочной горки на этапе принятия окончательного решения. Но целесообразность выбора той или иной схемы конструкции горочной горловины требует не меньшего внимания к их разработке.
Постановка цели и задач исследования
В учебном процессе транспортных вузов России студенты эксплуатационных специальностей и направлений используют типовые схемы горочных горловин при разработке курсовых и дипломных проектов, в которых предусматривается реконструкция и переустройство железнодорожных технических станций. Эти схемы они берут из, ставших уже классическими, альбомных учебных пособий [1], которые содержат малое число вариантов конструкций горочных горловин на фиксированное число путей в сортировочном парке. В действительности таких конструкций намного больше и их путевое развитие предусматривает укладку одинакового количества стрелочных переводов. Соответственно, различные конструкции горочных горловин будут иметь различную их длину.
В соответствии с Правилами и нормами проектирования сортировочных устройств [4] горочные горловины должны обеспечивать наименьшее расстояние пробегов от вершины горки до последней разделительной стрелки. Это требование соблюдается на стадии проектирования сортировочных горок, и соответствует критерию: разница между количеством путей в левой (правой) и правой (левой) частях горловины не должна превышать единицы.
Правила и нормы налагают еще одно требование к проектированию: одинаковое по возможности число стрелок. Но в 2005-м году профессор МИИТа Шубко В. Г. доказал, что число стрелок в горочной горловине не зависит от самой ее конструкции [7]. Иными словами, проектировщики могут составить различные варианты схем горочных горловин, но число стрелок у всех них останется неизменным.
Горочной горловины с различной длиной содержат различные параметры сортировочной горки: конструкционную высоту, величину скоростных уклонов, их длину и мощность тормозных средств, необходимую для регулирования скорости скатывания отцепов по продольному профилю. Поэтому целью нашего исследования является определение таких схем горловин на фиксированное число путей в сортировочном парке, длина которых была бы минимальна. Именно эти схемы повышают качество и безопасность сортировочного процесса, и уменьшают капитальные затраты на реконструкцию.
Для достижения поставленной цели требуется решить три задачи:
1. Определить все возможные варианты соединения путей сортировочного парка в конструкцию пучкообразной стрелочной улицы;
2. Провести сравнительный анализ этих горловин и выявить группы (кластеры), в которых длина сортировочной горки минимальна.
3. Дать предложения по проектированию горочных сортировочных устройств и увеличению числа путей в сортировочном парке при проведении реконструкционных мероприятий.
Решение первой задачи находится на стыке классической комбинаторики, теории графов и теории чисел. В частности, оно предусматривает составление вариантов горочных горловин как бинарных деревьев с помощью триангуляций выпуклых многоугольников. Решение второй проводится методом кластеризации K-средних, которая позволяет сгруппировать горочные горловины на подмножества (кластеры) таким образом, чтобы горловины из одного кластера были более похожи друг на друга, чем на горловины из других кластеров по критерию минимальной их длины.
Достижение поставленной цели позволит проектировщикам составить варианты реконструкции железнодорожных технических станций с улучшенными показателями работы, повысить безопасность сортировочного процесса, перерабатываемого на горках вагонопотока, и снизить затраты на реконструкцию.
Формулировка критерия расчета схем горочных горловин
В 2005-м году профессор МИИТа Шубко В. Г. (далее — В.Г.) опубликовал учебное пособие [7], в котором впервые изложил свои взгляды на теоретико-графовое представление конструкций путевого развития горловин станций, включая горочные горловины. В этой работе горочная горловина представляется в виде графа, в котором его вершины принимаются за центры стрелочных переводов, а ребра — за путевое развитие. В.Г. определил топологическую связь между числом путей роспуска, числом путей в сортировочном парке и числом стрелочных переводов. Интересно, что сама конструкция горочной горловины не зависит от числа стрелочных переводов, которые соединяют пути сортировочного парка в конструкцию пучкообразной стрелочной улицы. Иными словами, число стрелочных переводов остается неизменным при различных конструкциях горочной горловины.
Граф пучкообразной стрелочной улицы — ацикличное двоичное дерево. Кроме того, степень каждой его вершины не превосходит 3, что говорит о его бинарности. Комбинаторику горочных горловин мы произведем с учетом следующего критерия: разница между количеством путей в левой (правой) и правой (левой) частях горловины не должна превышать 1 при нечетном их числе (рис. 2).
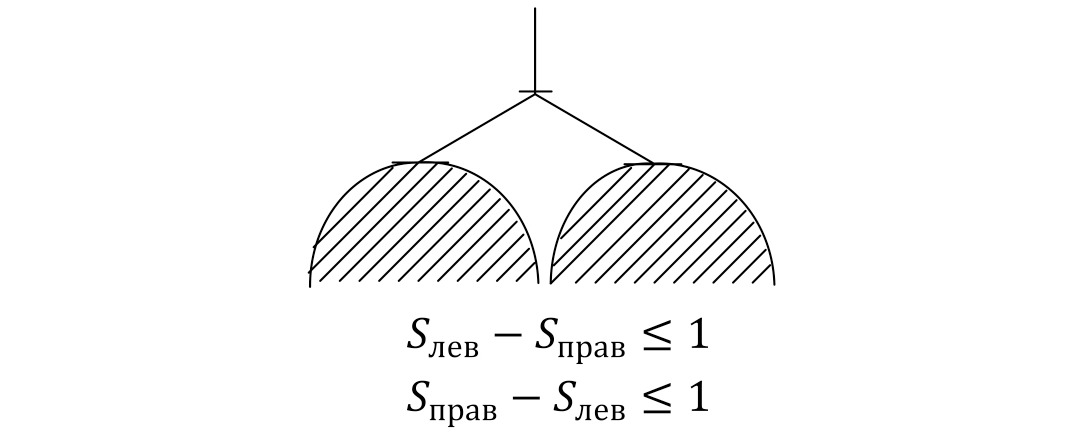
Схема сортировочной горки как алгебраическая полугруппа и триангуляция выпуклого многоугольника
Для комбинаторных расчетов горочную горловину возможно представить не только в виде графа-дерева, но и в виде простейшей алгебраической структуры, такой как полугруппа. Пусть существует некоторое множество X, которое состоит из n-го числа элементов. Мощность этого множества равняется мощности множества S путей в сортировочном парке. Зададим на множестве X бинарную операцию ∘:X×X×X→X, которая удовлетворяет условию ассоциативности: для любых x,y,z ∈X:x∘(y∘z) = (x∘y)∘z.
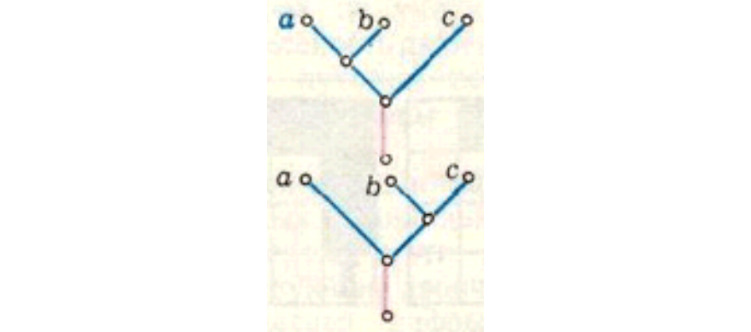
В полугруппе для множества, которое состоит из трех элементов условие ассоциативности предлагает два варианта расстановки скобок. Стрелочные переводы горочной горловины на три пути соединяют их в бинарное дерево также двумя вариантами (рис. 3).
Для вычисления всех возможных вариантов бинарных деревьев горочных горловин с фиксированным числом путей в сортировочном парке требуются все варианты расстановок скобок в бинарных операциях множества S. Их количество есть n-е число последовательности Каталана, которая широко используется в теории чисел и во многих комбинаторных задачах. Но не все бинарные деревья необходимы для представления конструкций горочных горловин, а только те, которые соответствуют указанному выше критерию: разница между числом путей в двух частях горочной горловины не должна превышать единицы.
Последовательность Каталана возможно определить также всеми возможными триангуляциями выпуклых многоугольников. Иными словами, многоугольник разбивается на треугольники непересекающимися диагоналями.
В качестве примера рассмотрим расчет числа вариантов конструкций пучкообразной стрелочной улицы с тремя путями в сортировочном парке с помощью триангуляции четырехугольника. В этом четырехугольнике число ребер равняется числу висячих вершин (путь роспуска и пути сортировочного парка), от которых отходит ровно одно ребро графа-дерева.
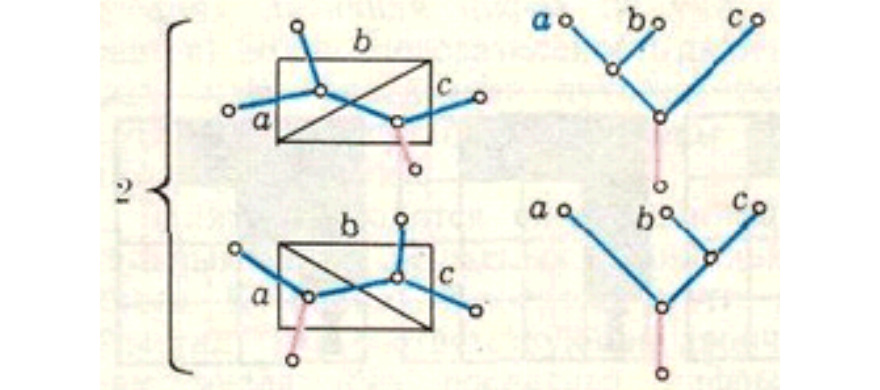
для определения числа вариантов горочных горловин
с 3-мя путями в сортировочном парке
Как видно из рис. 4 существует всего два способа разбить четырехугольник на треугольники. Нижнее ребро четырехугольника является основным: в него входит путь роспуска. Этот путь попадает в треугольник, который представляет собой первый разделительный элемент (стрелочный перевод) горочной горловины. Далее из этого треугольника путь может двигаться в двух направлениях: на путь сортировочного парка (проходя через один из катетов треугольника) и в следующий треугольник. Во втором треугольнике путь снова разобьется стрелочным переводов на два пути, затем пройдет через два катета этого треугольника и выйдет на оставшиеся два пути сортировочного парка. Таким образом, все ребра четырехугольника (за исключением нижнего ребра) представляют собой пути сортировочного парка.
Рассмотрим теперь пучкообразную стрелочную улицу с четырьмя путями в сортировочном парке. У нее всего один вариант соединения путей стрелочными переводами, так как она симметрична относительно левой и правой ее частей. Примечательно, что наблюдается всего один вариант соединения путей сортировочного парка, если их количество увеличивается по экспоненте. Иными словами, один вариант соединения будет у горочных горловин с 4, 8, 16, 32, 64, … путями.
Два критерия триангуляций выпуклого многоугольника для составления схем горочных горловин
Триангуляцию любого многоугольника, представляющего собой горочную горловину, мы будем производить, придерживаясь двух критериев:
1. При нечетном числе ребер в многоугольнике вершины его нижнего ребра необходимо соединить с самой дальней вершиной многоугольника;
2. При четном числе ребер в многоугольнике вершины его нижнего ребра необходимо соединить поочередно с двумя самыми дальними вершинами многоугольника.
Соблюдение этих двух критериев позволит триангулировать многоугольники таким образом, чтобы разница между числом путей в двух частях горочной горловины была минимальна. Этот минимум произойдет при триангуляции многоугольника с четным числом сторон. При нечетном же их числе количество путей в двух частях горловины будет одинаковым.
Рассмотрим теперь триангуляцию выпуклого шестиугольника, представляющего горочную горловину на 5 путей. В соответствии с последовательностью Каталана бинарное дерево на 5 путей имеет всего 14 вариантов соединения. Но, учитывая описанные нами критерии, конструкциям горочной горловины будут отвечать только 1, 4, 11 и 14 варианты триангуляций (рис. 5).
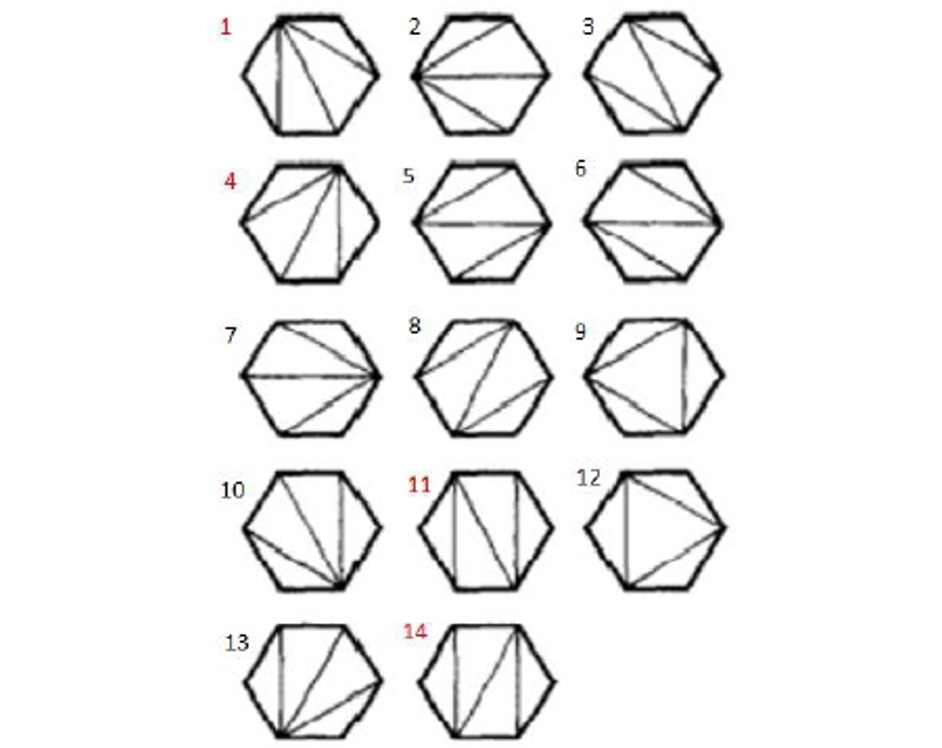
представляющих горочные горловины с 5 путями
в сортировочном парке, соответствует 1, 4, 11
и 14 варианты
Далее мы развиваем этот алгоритм для всех горочных горловин сортировочных устройств малой мощности, число путей в сортировочном парке которых ограничивается 16-ю. Особенность этого алгоритмического подхода — в индукционном методе вычисления (от простого к сложному): для определения схем горочных горловин с большим числом путей в сортировочном парке необходимо вначале определить схемы с меньшим числом путей. В Приложении 1 мы представили эти схемы. Примечательно, что их число меняется в зависимости от количества путей в сортировочном парке не линейно. Задача вычисления сводилась к ограничениям триангуляций многоугольников, то есть к ограничению вычисления последовательности Каталана.
Мы уже говорили о единственном варианте конструкции горочных горловин с 4, 8, 16, 32 и 64 путями. При расчете горловин с иным количеством путей, число которых не увеличивается по экспоненте, можно заметить особенность изменения числа вариантов конструкций: от экспоненты к экспоненте оно сначала увеличивается, затем уменьшается до одного.
Конструкция горочной горловины влияет на параметры сортировочной горки: конструктивную высоту, величину и длину скоростных уклонов и мощность тормозных средств. Компактная по длине горловина обеспечивает меньшую высоту сортировочной горки, а значит — и меньшую ее длину (расстояние от вершины горки до расчетной точки, которая в соответствии с [4] принимается на расстоянии не менее 50 метров от парковой тормозной позиции).
Определение схем горочных горловин горок малой мощности с минимальной длиной
Во второй задаче нашего исследования требуется определить конструктивные схемы горочных горловин, длина которых минимальна. Для этого выберем конструктивные параметры путевого развития горочных горловин, которые влияют на их длину. В соответствии с [4] таких параметров два: число путей в сортировочном парке и максимальное число стрелочных переводов на трудном по вписыванию пути. Анализ авторы провели для всех горочных горловин сортировочных устройств малой мощности, представленных в Приложении 1, методом кластеризации K-средних. Результаты исследования (табл. 1) показали что все горочные горловины с 15-ю путями в сортировочном парке имеют наибольшую длину из всех возможных схем, превышая при этом длину горловины с большим числом путей (16 путей).
Табл. 1
Кластеризация горочных горловин по их длине
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
