
Бесплатный фрагмент - Как устроен мир
Алгоритмы цифровой Вселенной

Глава 1. Формулирование проблемы
Множество умов человечества думало над вопросом — как же устроен мир? Предполагалось, что ответ должен быть, но каждая попытка построения теории приводила к специальной научной дисциплине, а решения в общеприменимом виде не находилось.
Науки, которые занимались проблемой устройства мира:
Геометрия и математика;
Астрономия;
Химия и физика;
Биология и медицина;
Философия, теология и смежные области знаний;
Электродинамика в части теории поля;
Космология.
И какие результаты? Можно сказать, что они весьма обрывочны и непонятны. В массовое сознание одновременно входят и теологические теории с их божественным происхождением мира и теории физические — типа «большой взрыв», «расширяющаяся вселенная» и их аналоги.
Как-то непонятно положение современной химии — вопросы атомного и, тем более субатомного, строения вещества перешли к физикам, наверное, навсегда.
Классическая философия тем более оттеснена от передовых рубежей, вроде бы победил материализм, но это своего рода традиция не более того.
Классических математиков вспоминают, когда необходимо что-то решить, но не как источников гипотез, хотя роль геометрии и топологии должна быть в понимании строения пространства большой, если не решающей.
Вопрос — существует ли единая математическая гармония мира — потерял свою актуальность под напором множества эмпирических законов физики, химии и разделов этих наук. В некотором смысле математики согласились, что единой математической гармонии нашего мира не существует. Так ли это?
Очень странное положение занимает современная биология — теория Дарвина официально и не опровергнута и молчаливо критикуется, а каждое новое достижение генетики ее якобы опровергает, место ботаники занимает генная инженерия.
Из астрономии как-то сама собой выделилась космология — и она существует как отдельная наука, сама же астрономия больше напоминает астрономическую статистику. Укрепился, и серьезно, авторитет астрологии.
Основное свойство современной научно-философской мысли — узкоспециальная глубина, но разрозненность и мозаичность научных и философских знаний.
Цель этой книги — по возможности объяснить, как устроен наш мир, и показать математические и физические основы строения мира.
Методика данной книги — сначала привести новые математические выкладки, после этого обосновать эти математические выкладки физическими фактами и сведениями, применяя цитаты из книг известных ученых, в завершение сделать выводы.
Основанная позиция автора:
не опровергать, а объяснять;
не доказывать голословно, а показать достижения ученых, в большинстве случаев сопровождая это прямыми отсканированными цитатами;
не навязывать свое мнение, а предлагать факты, которые давно обнаружены учеными, но не очень широко известны простым людям.
Обратимся к двум цитатам от великих естествоиспытателей, и одной от физика середины 20-го века.
1.1. Роль научной теории
Прекрасно сказал физик Шредингер о роли научной теории — я полностью согласен с его глубокой мыслью [1]. Цитата, стр. 95.

1.2. Понятие «естественный»
Понятие «естественный», которое я широко использую, применительно к природе блестяще предложил Дарвин в одном из эпиграфов своей знаменитой книги [2].
«Единственное определение значения слова „естественный“ это — установленный, фиксированный или упорядоченный; ибо, не есть ли естественное то, что требует или предполагает разумного агента, который делает его таковым, то есть осуществляется им постоянно или в установленное время, точно так же как сверхъестественное или чудесное — то, что осуществляется им только однажды».
Откровенна позиция известного физика Джеммера, который признается — понятие масса, которое автор данной книги задает новой формулой в одной из своих книг, в современной официальной физике «опутано серьезными неопределенностями» [3].

Глава 2. Пирамида чисел Фибоначчи — Кучина
Читатель вправе задать вопрос — серьезно ли пишет автор о своей претензии на открытие математической гармонии мира? В своем ли он уме? Нет ли в его работе мистификации и обмана?
Что мне ответить. Все что я пишу — абсолютно серьезно. Мне действительно удалось 13 июля 2008 года первому провести построение математического ряда, который я назвал естественным, и числа которого оказались широко представлены в физической структуре нашего мира. В данной работе я покажу иной метод построения этого ряда Кучина и продемонстрирую его десятичную связь с рядом Фибоначчи.
2.1. О Фиббоначчи
Кто такой Фибоначчи нам поможет понять цитата из истории Стройка. [4].

2.2. Поиск закономерностей
На вопрос — нужно ли искать закономерности в строении мира я отвечу цитатой из книги математика Сойера [5]. Математик Сойер точно обозначает цель моей работы — именно отталкиваясь от изоморфизма и наблюдая поразительное повторение чисел из естественного ряда Кучина в разных областях нашего мира, я пришел к стойкому убеждению в наличии не мистической, а математической закономерности.

2.3. Построение пирамиды чисел Фибоначчи — Кучина
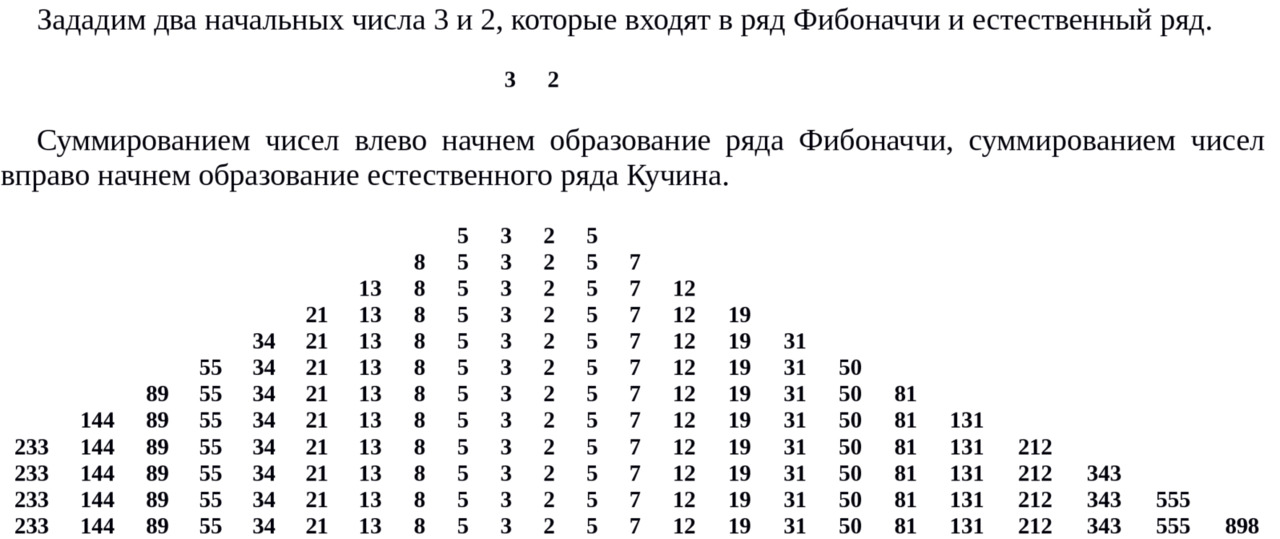
Проведем «пирамидальное построение ряда Кучина с одновременным построением ряда чисел Фибоначчи. Задачу будем решать поэтапно. Для наглядности применим таблицу. Перед нами числа из ряда Фибоначчи и ряда Кучина. Числа в левой части числовой пирамиды — это ряд Фибоначчи, в правой части пирамиды — естественный ряд Кучина.
2.4. Десятичная связь ряда Кучина с рядом Фибоначчи
Обратим внимание на удивительную математическую особенность — если число естественного ряда Кучина (от 12 до 898) разделить на 10 и оставить целую часть числа — мы получим число из ряда Фибоначчи!
Проверим это на начальных представленных в таблице числах рядов:
— число 19 — 1,9 — 2 — число ряда Фибоначчи 2;
— число 31 — 3,1 — 3 — число ряда Фибоначчи 3;
— число 50 — 5,0 — 5 — число ряда Фибоначчи 5;
— число 81 — 8,1 — 8 — число ряда Фибоначчи 8;
— число 131 — 13,1 — 13 — число ряда Фибоначчи 13;
— число 212 — 21,2 — 21 — число ряда Фибоначчи 21;
— число 343 — 34,3 — 34 — число ряда Фибоначчи 34;
— число 555 — 55,5 — 55 — число ряда Фибоначчи 55;
— число 898 — 89,8 — 89 — число ряда Фибоначчи 89;
Таким образом, ряды Фибоначчи и естественный ряд Кучина — математические родственники, но ряд Кучина более точный, а его члены встречаются в нашем физическом мире непосредственно в абсолютных значениях. Покажем правильность первого утверждения.
2.5. Золотое сечение
Как известно числа ряда Фибоначчи относятся приблизительно как число Фидия, или «золотое сечение». Почитаем раздел из БСЭ [6].
Отношение сторон по «золотому сечению» (согласно чертежу) х=0,62. Но если мы применим числа Фибоначчи 5 и 8, то получим результат 5/8=0,6, в тоже время числа ряда Кучина, например 31 и 50, дадут более точный результат 31/50=0,62.
Правильность второго утверждения о повсеместной применимости чисел естественного ряда Кучина будет показана в следующей главе. Автор приведет примеры из физических законов и цитаты из книг естествоиспытателей разных эпох.
Поиски нахождения чисел из ряда Фибоначчи в нашем мире, т.е. 13, 21, 34, 55, 89, 144, и т. д. автор предоставляет читателям, но он заявляет — эти числа в абсолютном значении в физических законах не встречаются.
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.