Бесплатный фрагмент - История развития некоторых математических понятий

Введение

История развития математики — это не только история развития математических идей, понятий и направлений, но это и история взаимосвязи математики с человеческой деятельностью, социально-экономическими условиями различных эпох. Становление и развитие математики как науки, возникновение ее новых понятий и разделов тесно связано с развитием потребностей общества в измерениях. Первые области применения математики были связаны с созерцанием звезд и земледелием. Изучение звездного неба позволило проложить торговые морские пути, караванные дороги в новые районы и резко увеличить эффект торговли между государствами. Обмен товарами приводил к обмену культурными ценностями, к развитию толерантности как явления, лежащего в основе мирного сосуществования различных рас и народов.

Математика придавала законченный вид всем наукам, где бы она применялась. В Европе сложилось разделение на гуманитарные и естественные науки по степени влияния математики на эти части. Потребности измерения (количества зерна, длины дороги и т. п.) приводят к появлению названий и обозначений простейших дробных чисел и к разработке приёмов выполнения арифметических действий над дробями. Таким образом, накапливался материал, складывающийся постепенно в древнейшую математическую науку — арифметику. Измерение площадей и объёмов, потребности строительной техники, а несколько позднее — астрономии, вызывают развитие начатков геометрии. Эти процессы шли у многих народов в значительной мере независимо и параллельно.

Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа есть качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, годы. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.

Распространение понятий и принципов математики в различные сферы научного познания оказывает существенное влияние, как на эффективность специальных исследований, так и на развитие самой математики. В процессе познания действительности математика играет все более возрастающую роль. Сегодня нет такой области знаний, где в той или иной степени не использовались бы математические понятия и методы. Проблемы, решение которых раньше считалось невозможным, успешно решаются благодаря применению математики, тем самым расширяются возможности научного познания.

История математики и культуры в целом накопила огромный материал, убедительно свидетельствующий о практическом происхождении исходных понятий и методов таких древнейших отраслей математического знания, какими являются арифметика и геометрия. В дальнейшем, переход от математики постоянных величин к математике переменных величин приведший к созданию математического анализа в форме дифференциального и интегрального исчисления, был создан аппарат математики переменных величин. В свою очередь запросы механики и астрономии были вызваны потребностями зарождавшегося капиталистического общества, развитием его мощных производительных сил, переходом от ручного труда к машинному производству. То же самое можно сказать о новейшей революции в математике, которая характеризуется дальнейшим расширением области исследования математики, переходом от изучения зависимостей между величинами к исследованию абстрактных структур самого разнообразного вида. Создание ЭВМ расширило возможности в науке, в экономике, технике и других областях знаний. Такое широкое применения математических методов являются результатом мощного развития науки и техники, приведшим к современной научно-технической революции.

В ходе развития математики, дифференциация сопровождается диалектически ей противоположным процессом интеграции знаний, которая приводит к возникновению новых интеграции теорий. Такие теории представляют собой синтез двух или нескольких теорий или научных дисциплин. Наиболее известным примером служит аналитическая геометрия, в которой алгебраические методы были использованы для изучения геометрических фигур. Сейчас наиболее впечатляющим примером синтеза идей, идущих от алгебры, геометрии, математического анализа и топологии, служит функциональный анализ, получивший широкое применение в современной теоретической физике. Эти и другие примеры говорят о том, что интеграция знаний служит важным источником внутреннего развития математики, способствуя возникновению новых более глубоких и общих теорий и математических дисциплин. Концептуальное обобщение понятий служит одним из основных источников развития математики, т.к. в результате этого существенно меняется значение и объем прежнего понятия и тем самым знакомым примером такого обобщения является возникновение понятий рациональных, действительных и комплексных чисел. Все эти понятия можно рассматривать как последовательные обобщения натурального числа. Поскольку обобщения происходят обычно в рамках определенных теорий, то с равным основанием можно говорить такие обобщения математических теорий. При этом, во-первых, происходит расширение области применения новой обобщенной теории, а во- вторых, сохраняется связь преемственность между новой и старой теорией.

Данная работа рассматривает некоторые концепции возникновения и развития математических понятий и символов. В содержании рассматриваются первоначальные геометрические понятия в планиметрии, первоначальные геометрические понятия в стереометрии, первоначальные понятия о числе, возникновение символов в математике.

1 Возникновение и развитие числовых понятий

1.1 Первоначальные понятия о числе

Интуитивное представление о числе, по-видимому, так же старо, как и само человечество, хотя с достоверностью проследить все ранние этапы его развития в принципе невозможно. Прежде чем человек научился считать или придумал слова для обозначения чисел, он, несомненно, владел наглядным, интуитивным представлением о числе, позволявшим ему различать одного человека и двух людей или двух и многих людей. То, что первобытные люди сначала знали только «один», «два» и «много», подтверждается тем, что в некоторых языках, например, в греческом, существуют три грамматические формы: единственного числа, двойственного числа и множественного числа. Позднее человек научился делать различия между двумя и тремя деревьями и между тремя и четырьмя людьми. Счет изначально был связан с вполне конкретным набором объектов, и самые первые названия чисел были прилагательными. Например, слово «три» использовалось только в сочетаниях «три дерева» или «три человека»; представление о том, что эти множества имеют между собой нечто общее — понятие троичности — требует высокой степени абстракции. О том, что счет возник раньше появления этого уровня абстракции, свидетельствует тот факт, что слова «один» и «первый», равно как «два» и «второй», во многих языках не имеют между собой ничего общего, в то время как лежащие за пределами первобытного счета «один», «два», «много», слова «три» и «третий», «четыре» и «четвертый» ясно указывают на взаимосвязь между количественными и порядковыми числительными. Первоначальные представления о числе появились в эпоху каменного века, при переходе от простого собирания пищи к ее активному производству, примерно 100 веков до н. э. В математике нет компонента важнее. Несмотря на это, число как понятие развивалось на протяжении не одной тысячи лет, пока ученые умы всего мира не договорились-таки о том, как воспринимать его. Первые прикладные дисциплины, которые настоятельно требовали появления этого понятия, были связаны с земледелием, строительством и наблюдениями за звездами. В свою очередь, изучение звездного неба и классификация всех измерений были жизненно необходимы для развития судоходства и международной торговли, без которой не могло развиваться ни одно государство.

Немного философии. Даже самые примитивные цифры вырабатывались и приводились к единому виду на протяжении многих веков. Многие из них образовались в результате творческого переосмысления слов или отдельных букв. Знаменитый Пифагор говорил, что цифры являются тем таинственным, эфемерным веществом, из которого образована вся Вселенная. В общем-то, согласно современным представлениям науки, он был во многом прав. Китайцы делили числа на две большие категории (которые сохранились и по сей день): Нечетные, или Ян. В древнекитайской философии они символизировали небо и благоприятность. Соответственно, четные (Инь). Это понятие символизировало землю и нестабильность.

Числовые термины тяжело зарождались и медленно входили в употребление. Древнему человеку было далеко до абстрактного мышления, хватило того, что он придумал числа: «один» и «два». Остальные количества для него оставались неопределенными и объединялись в понятии «много». Росло производство пищи, добавлялись объекты, которые требовалось учитывать в повседневной жизни, в связи с чем придумывались новые числа: «три», «четыре»… Долгое время пределом познания было число «семь». О непонятном говорили, что эта книжка «за семью печатями», знахарки в сказках давали больному «семь узелков с лекарственными травами, которые надо было настоять на семи водах в течение семи дней и принимать каждодневно по семь ложек». Познаваемый мир усложнялся, требовались новые числа. Так дошли до нового предела. Им стало число 40. Запредельные количества моделировались громадным по тем временам числом «сорок сороков», равным 1600. Позднее, когда число «сорок» уже перестало быть граничным, оно стало играть большую роль в русской метрологии как основа системы мер: пуд имел 40 фунтов, бочка-сороковка — сорок ведер и т. д.

Большой интерес вызывает история числа «шестьдесят», которое часто фигурирует в вавилонских, персидских и греческих легендах как синоним большого числа. Вавилоняне считали его Божьим числом: шестьдесят локтей в высоту имел золотой идол из храма вавилонского царя Навуходоносора. Позже с тем же самым значением (неисчислимое множество) возникли числа, кратные 60: 300, 360. Со временем число 60 в Вавилоне легло в основу шестидесятеричной системы исчисления, следы которой сохранились до наших дней при измерении времени и углов.

Пределом у славян было число «тьма», у древних греков — мириада, равное 10 000, а запределом — «тьма тьмущая», равное 100 миллионам. У славян применяли также и иную систему исчисления. так называемое «большое число» или «большой счет». В этой системе «тьма» равнялась 106, «легион» — 1012, «леодр» — 1024, «ворон» — 1048, «колода» — 1096, после чего добавляли, что большего числа не существует. В Античном мире дальше всех продвинулись Архимед (III в. до н.э.) в «исчислении песчинок» — до числа 10, возведенного в степень 8х1016, и Зенон Элейский (IV в. до н. э.) в своих парадоксах — до бесконечности ∞.

Названия чисел, выражающие весьма абстрактные идеи, появились, несомненно, позже, чем первые грубые символы для обозначения числа объектов в некоторой совокупности. В глубокой древности примитивные числовые записи делались в виде зарубок на палке, узлов на веревке, выложенных в ряд камешков, причем подразумевалось, что между пересчитываемыми элементами множества и символами числовой записи существует взаимно однозначное соответствие. Но для чтения таких числовых записей названия чисел непосредственно не использовались. Ныне мы с первого взгляда распознаем совокупности из двух, трех и четырех элементов; несколько труднее распознаются на взгляд наборы, состоящие из пяти, шести или семи элементов, а за этой границей установить на глаз их число практически уже невозможно, и нужен анализ либо в форме счета, либо в определенном структурировании элементов.

Счет на бирках, по-видимому, был первым приемом, который использовался в подобных случаях: зарубки на бирках располагались определенными группами подобно тому, как при подсчете избирательных бюллетеней их часто группируют пачками по пять или десять штук. Очень широко был распространен счет на пальцах, и вполне возможно, что названия некоторых чисел берут свое начало именно от этого способа подсчета. Важная особенность счета заключается в связи названий чисел с определенной схемой счета. Например, слово «двадцать три» — не просто термин, означающий вполне определенную (по числу элементов) группу объектов; это термин составной, означающий «два раза по десять и три». Здесь отчетливо видна роль числа десять как коллективной единицы или основания; и действительно, многие считают десятками, потому что, как отметил еще Аристотель, у нас по десять пальцев на руках и на ногах. По той же причине использовались основания пять или двадцать. На очень ранних стадиях развития истории человечества за основания системы счисления принимались числа 2, 3 или 4; иногда для некоторых измерения или вычислений использовались основания 12 и 60. Считать человек начал задолго до того, как он научился писать, поэтому не сохранилось никаких письменных документов, свидетельствовавших о тех словах, которыми в древности обозначали числа. Возникла и необходимость в системе записи чисел, и именно тогда было заложено основание для развития математики.

Первоначальные представления о числе и форме относятся к очень отдаленной эпохе древнего каменного века — палеолита. В течение сотен тысячелетий этого периода люди жили в пещерах, в условиях, мало отличавшихся от жизни животных, и их энергия уходила преимущественно на добывание пищи простейшим способом — собиранием ее, где только это было возможно. Люди изготовляя орудия для охоты и рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднего палеолита украшали свое существование, создавая произведения искусства, статуэтки и рисунки; Возможно, рисунки в пещерах Франции и Испании давности порядка 15 тысяч лет, имели ритуальное значение, но, несомненно, в них обнаруживается замечательное чувство формы.

Пока не произошел переход от простого собирания пищи к активному ее производству, от охоты и рыболовства к земледелию, люди мало продвинулись в понимании числовых величин и пространственных отношений. Лишь с наступлением. этого фундаментального перелома, переворота, когда пассивное отношение человека к природе сменилось активным, мы вступаем в новый, каменный век — в неолит. Это великое событие в истории человечества произошло примерно десять тысяч лет тому назад, когда ледяной покров в Европе и Азии начал таять и уступать место лесам и пустыням. Постепенно прекращались кочевые странствия в поисках пищи. Рыболовы и охотники все больше вытеснялись первобытными земледельцами. Такие земледельцы, оставаясь на одном месте, пока почва сохраняла плодородие, строили жилища, рассчитанные на более долгие сроки. Стали возникать деревни для защиты от непогоды и от врагов-хищников. Немало таких неолитических поселений раскопано. По их остаткам видно, как постепенно развивались такие простейшие ремесла, как гончарное, ткацкое и плотничье. Существовали житницы, так что население могло, производя излишки, запасать продукты на зиму и на случай неурожая. Выпекали хлеб, варили пиво, в эпоху позднего неолита плавили и обрабатывали медь и бронзу. Совершались открытия, были изобретены гончарный круг и тележное колесо, совершенствовались лодки и жилища. Все эти замечательные новшества возникали лишь в пределах той или иной зоны и не всегда распространялись вне ее. Тем не менее, темп технического прогресса в колоссальной мере ускорился по сравнению с древним каменным веком. Деревни вели между собой значительную торговлю, которая настолько развилась, что можно проследить наличие торговых связей между областями, удаленными на сотни километров друг от друга. Эту коммерческую деятельность сильно стимулировали открытия техники выплавки меди и бронзы и изготовление сначала медных, а затем бронзовых орудий и оружия, что в свою очередь содействовало дальнейшему формированию языков. Слова этих языков выражали вполне конкретные вещи и весьма немногочисленные абстрактные понятия, но языки уже имели известный запас слов для простых числовых терминов и для некоторых пространственных образов.

Числовые термины, выражающие некоторые из «наиболее абстрактных понятий, какие в состоянии создать человеческий ум», как сказал Адам Смит, медленно входили в употребление. Впервые они появляются скорее как качественные, чем количественные термины, выражая различие лишь между одним или, вернее, «каким-то» — «какой-то» скорее, чем «один человек» и двумя и многими. Древнее качественное происхождение числовых понятий и сейчас еще выявляется в тех особых двоичных терминах, которые имеются в некоторых языках, как, например, в греческом и кельтском.

С расширением понятия числа большие числа сначала образовывались с помощью сложения: 3 путем сложения 2 и 1, 4 путем сложения 2 и 2, 5 путем сложения 2 и 3. Вот примеры счета некоторых австралийских племен: племя реки Муррей: 1 энэа, 2 равно петчевал, 3 равно петчевал-энэа, 4 — петчевал-петчевал. Камиларои считали так: 1 мал, 2 равно булан, 3 равно гульба, 4 — булан-булан, 5 — булан-гульба, 6 — гульба-гульба.

Развитие ремесла и торговли содействовало кристаллизации понятия числа. Числа группировали и объединяли в большие единицы, обычно пользуясь пальцами одной руки или обеих рук — обычный в торговле прием. Это вело к счету сначала с основанием пять, потом с основанием десять, который дополнялся сложением, а иногда вычитанием, так что двенадцать воспринималось, как (10+2), а девять, как (10–1). Иногда за основу принимали 20, число пальцев на руках и ногах. Из триста семи систем исчисления первобытных американских народов, исследованных Илсом (W. С. Eels), сто сорок шесть были десятичными, сто шесть — пятичными и пятичными-десятичными, остальные были двадцатичными и пятично-двадцатичными. В наиболее характерной форме система с основанием двадцать существовала у майя в Мексике и у кельтов в Европе. Числовые записи велись с помощью пучков, зарубок на палках, узлов на веревках, камешков или ракушек, сложенных по пять в кучки, приемами, весьма схожими с теми, к каким в давние времена прибегал хозяин постоялого двора, пользовавшийся бирками. Для перехода от таких приемов к специальным символам для 5, 10, 20 и так далее, надо было сделать лишь один шаг, и именно такие символы мы обнаруживаем в пользовании в начале истории, на так называемой заре цивилизации. Древнейший пример пользования бирками приходится на эпоху палеолита. Обнаруженная в 1937 г. в Вестонице (Моравия) лучевая кость молодого волка длиной около 17 сантиметров с 55 глубокими зарубками является примером такой бирки. Первые двадцать пять зарубок размещены группами по пять, за ними идет зарубка двойной длины, заканчивающая этот ряд, а затем с новой зарубки двойной длины начинается новый ряд из зарубок.

Пальцевой счет, то есть счет пятками и десятками, возник только на известной ступени общественного развития. Но раз до этого дошли, появилась возможность выражать числа в системе счисления, что позволяло образовывать большие числа. Так возникла примитивная разновидность арифметики. Четырнадцать выражали как (10+4), иногда как (15–1). Умножение зародилось тогда, когда 20 выразили не как (10+10), а как (2*10). Подобные двоичные действия выполнялись в течение тысячелетий, представляя собой нечто среднее между сложением и умножением, в частности в. Египте и в доарийской культуре Мохенджо-Даро на Инде. [8]

Деление началось с того, что 10 стали выражать как «половину тела», хотя сознательное применение дробей оставалось крайне редким явлением. Например, у североамериканских племен известны только немногие случаи применения дробей, и почти всегда это только дробь ½, хотя иногда встречаются 1/3 и 1/4). Любопытно, что люди увлекались очень большими числами, к чему, может быть, побуждало общечеловеческое желание преувеличить численность стада или убитых врагов; пережитки такого уклона заметны в библии и в других религиозных книгах.

Возникла необходимость измерять длину и емкость предметов. Единицы измерения были грубы, и при этом часто исходили из размеров человеческого тела. Об этом нам напоминают такие единицы, как палец, фут (то есть ступня), локоть. Когда начали строить дома такие, как у земледельцев Индии или обитателей свайных построек Центральной Европы, стали вырабатываться правила, как строить по прямым линиям и под прямым углом. Английское слово «straight» (прямой) родственно глаголу «stretch» (натягивать), что указывает на использование веревки. Английское слово «line» (линия) родственно слову «linen» (лен), что указывает на связь между ткацким ремеслом и зарождением геометрии, таков был один из путей, по которому шло развитие математических интересов.

Человек неолита обладал также острым чувством геометрической формы. Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок, корзин и тканей, позже — обработка металлов вырабатывали представление о плоскостных и пространственных соотношениях. Должны были сыграть свою роль и танцевальные фигуры. Неолитические орнаменты радовали глаз, выявляя равенство, симметрию и подобие фигур. В этих, фигурах могут проявляться и числовые соотношения, как в некоторых доисторических орнаментах, изображающих треугольные числа; в других орнаментах обнаруживаем «священные» числа. Этот орнамент встречается на неолитической керамике из Боснии и на предметах искусства древней Месопотамии. Такого рода орнаменты оставались в исторические времена. [26]

Прекрасные образцы мы видим на дипилоновых вазах раннегреческого периода, позже — в византийской и арабской мозаике, в персидских и китайских коврах. Первоначально ранние орнаменты, возможно, имели религиозное или магическое значение, но постепенно преобладающим стало их эстетическое назначение. В религии каменного века можно уловить первые попытки вступить в борьбу с силами природы. Религиозные обряды были насквозь пронизаны магией, магический элемент входил в состав существовавших тогда числовых и геометрических представлений, проявляясь также в скульптуре, музыке, рисунке. Существовали магические числа такие, как 3, 4, 7, и магические фигуры, как, например, пятиконечная звезда и свастика. Такие орнаменты были в ходу у жителей свайных построек близ Любляны (Югославия) Гальштатского периода (Центральная Европа, 1000 — 500 до н. э.).

Некоторые авторы даже считают, что магическая сторона математики были решающим фактором в ее развитии, но с этим можно поспорить. Хотя общественные корни математики в новейшие времена, быть может, стали менее заметны, они вполне очевидны в раннем периоде истории человечества. Современная «нумерология» — пережиток магических обрядов, восходящих к неолитической, а может быть, даже к палеолитической эпохе. Также у многих племен мы находим какой-то отсчет времени и, следовательно, какие-то сведения о движении Солнца, Луны и звезд. Сведения этого рода впервые приобрели более научный характер, когда стали развиваться земледелие и торговля. Пользование лунным календарем относится к очень давней эпохе в истории человечества, так как изменение в ходе произрастания растений связывали с фазами Луны. Примитивные народы обратили внимание и на солнцестояние, и на восход Плеяд в сумерках. Самые древние цивилизованные народы относили астрономические сведения к наиболее отдаленному, доисторическому периоду своего существования. Другие первобытные народы пользовались при плавании созвездиями как ориентирами. Эта астрономия дала некоторые сведения о свойствах сферы, окружностей, об углах. Краткие сведения из эпохи зарождения математики показывают, что наука в своем развитии не проходит обязательно все те этапы, из которых теперь складывается ее преподавание. Лишь недавно ученые обратили должное внимание на некоторые из древнейших известных человечеству геометрических фигур такие, как узлы или орнаменты.

Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом пальцы рук и ног. Наскальный рисунок, сохранившийся до наших времен от каменного века, изображает число 35 в виде серии выстроенных в ряд 35 палочек-пальцев. Первыми существенными успехами в арифметике стали концептуализация числа и изобретение четырех основных действий: сложения, вычитания, умножения и деления. Первые достижения геометрии связаны с такими простыми понятиями, как прямая и окружность. Развитие земледелия, отношений земельной собственности требуют умения измерять расстояния, площади земельных участков, отсюда и происхождение слова «геометрия» от древнегреческого «землемерие». [31]

В строительстве необходимо было освоить проведение прямых горизонтальных и вертикальных линий, построение прямых углов и т. д. Прямая натянутая веревка служила прообразом представления о прямой геометрической линии. Одним из важнейших свидетельств освоения человеком в эту эпоху геометрических абстракций является зафиксированный археологами бурный всплеск орнаментальной изобразительной деятельности, геометрических орнаментов на сосудах, на ткани, на одежде. Геометрическая отвлеченность начинает превалировать в художественной изобразительной деятельности, в передаче изображений животных, растений, человека. Счёт предметов на самых ранних ступенях развития культуры привёл к созданию простейших понятий арифметики натуральных чисел. Натуральные числа имеют две основные функции: характеристика количества предметов и характеристика порядка предметов, размещенных в ряд. В соответствии с этими функциями возникли понятия порядкового числа (первый, второй и т.д.) и количественного числа (один, два и т.д.).

Долго и трудно человечество добиралось до первого уровня обобщения чисел. Сто веков понадобилось, чтобы выстроить ряд самых коротких натуральных чисел от единицы до бесконечности: 1, 2, … ∞. «Натуральных» потому, что ими обозначались реальные неделимые объекты: люди, животные, вещи… Только на основе разработанной системы устного счисления возникают письменные системы счисления и постепенно вырабатываются приёмы выполнения над натуральными числами четырёх арифметических действий, из которых только деление ещё долго представляло большие трудности.

В рассматриваемую эпоху основные направления развития математических знаний следующие. Во-первых, это расширение пределов считаемых предметов. Появляются словесные обозначения для чисел свыше 100 единиц, сначала до 1000, а затем вплоть до 10000. Во-вторых, закладываются предпосылки позиционной системы счисления. Они состояли в совершенствовании умения считать не единицами, а сразу некоторым набором единиц. Когда нужно было пересчитать большое количество одинаковых предметов, стадо скота, например, применялся так называемый групповой счет. Такой счет вело несколько человек. Один — вел счет единицам, второй — десяткам, третий — сотням. Развитие хозяйства, торговли требовало не просто умения считать, но и умения сохранять на длительное время или передавать на расстояния результаты счета, очень часто — большие числа. Для этого применяются известные еще с древнейших времен бирки, шнуры, нарезки или узлы, на которых уже обозначаются не только единицы, но и группы единиц (по 4, 5, 10, 20 единиц). По сути, этим формировался прообраз различных систем счисления. Третьим важным направлением развития математических знаний в рассматриваемую эпоху является формирование простейших геометрических абстракций — прямой линии, угла, объема и других.

1.2 Натуральные и целые числа

Существует большое количество определений понятию «число» Первое научное определение числа дал Эвклид в своих «Началах», которое он, очевидно, унаследовал от своего соотечественника Эвдокса Книдского (около 408 — около 355 гг. до н. э.): «Единица есть то, в соответствии с чем каждая из существующих вещей называется одной. Число есть множество, сложенное из единиц». Так определял понятие числа и русский математик Магницкий в своей «Арифметике» (1703 г.). Раньше Эвклида Аристотель дал такое определение: «Число есть множество, которое измеряется с помощью единиц». Со слов греческого философа Ямвлиха, еще Фалес Милетский — родоначальник греческой стихийно-материалистической философии, учил, что «число есть система единиц». Это определение было известно и Пифагору. Считается, что термин «натуральное число» впервые применил римский государственный деятель, философ, автор трудов по математике и теории музыки Боэций (480 — 524 гг.), но до него греческий математик Никомах из Геразы говорил о натуральном, то есть природном ряде чисел. Понятием «натуральное число», в современном его понимании, последовательно пользовал выдающийся французский математик, философ-просветитель Даламбер (1717–1783 гг.).

Понятие числа в математике может относиться к объектам различной природы: натуральным числам, используемым при счете, числам являющимся возможными результатами (идеализированных) измерений, отрицательным числам, мнимым числам и к другим более абстрактным классам чисел, используемым в высших разделах математики, например, к гиперкомплексным и трансфинитным числам. Число необходимо отличать от его символа, или обозначения, которое его представляет. Рассмотрим логические отношения между различными классами чисел. Элементарная арифметика оперирует с положительными целыми числами и нулем, с дробями, в известной мере с положительными действительными числами, и иногда с отрицательными действительными числами. Более сложные действия над отрицательными и мнимыми числами обычно принято относить к компетенции алгебры. [4]

Правила, осваиваемые при изучении арифметики, применимы без каких-либо ограничений только к положительным действительным числам, поэтому некоторые действия, производимые над более общими классами чисел, часто кажутся «загадочными», например,

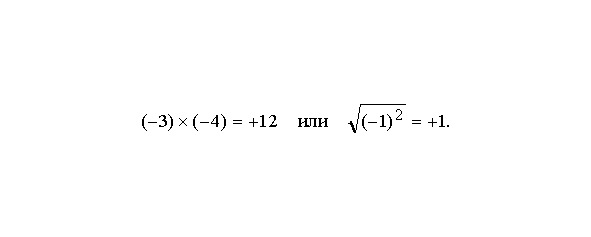
Такие загадки легко разрешаются, если принять во внимание, что различные классы чисел имеют совершенно различный смысл. Хотя у них достаточного много общего, чтобы их всех можно было называть числами, не следует думать, что все они будут удовлетворять одним и тем же правилам.

Рассмотрим положительные целые числа. Мы все усваиваем положительные целые числа (1, 2, 3 и т.д.) в раннем детстве, когда вряд ли приходит в голову задумываться об определениях, тем не менее, такие числа могут быть определены по всем правилам формальной логики. Строгое определение числа 1 заняло бы не один десяток страниц, а формула типа 1 +1 = 2, если записать ее во всех подробностях без каких-либо сокращений, протянулась бы на несколько километров. Однако любая математическая теория вынуждена начинаться с некоторых неопределяемых понятий и аксиом или постулатов относительно них. Так как положительные целые числа хорошо известны и трудно определить их с помощью чего-то более простого, примем их за исходные неопределяемые понятия и будем считать, что основные свойства этих чисел известны.

Далее, при изучении математики идут отрицательные целые числа и нуль. Отрицательные числа в наши дни вещь обыденная, их используют, например, для того, чтобы представить температуру ниже нуля. Поэтому кажется удивительным, что еще несколько столетий назад какой-либо конкретной интерпретации отрицательных чисел не было, а возникающие по ходу вычислений отрицательные числа назывались «воображаемыми». Обходиться только натуральными числами не всегда удобно. Например, ими нельзя вычесть большее из меньшего. Для такого случая и были введены отрицательные числа: китайцами — в Х веке до н. э., индийцами — в VII веке, европейцами — только в XIII веке. Положительные количества в китайской математике называли «чен», отрицательные — «фу»; их изображали разными цветами: «чен» — красным, «фу» — черным. Такой способ изображения использовался в Китае до середины XII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел — цифры, которые изображали отрицательные числа, перечеркивали черточкой наискось справа налево.

В V–VI столетиях отрицательные числа появляются и очень широко распространяются в индийской математике. В Индии отрицательные числа систематически использовали в основном так, как это мы делаем сейчас. Уже в произведении выдающегося индийского математика и астронома Брахмагупты (598 — 660 гг.) читаем: « имущество и имущество есть имущество, сумма двух долгов есть долг; сумма имущества и нуля есть имущество; сумма двух нулей есть нуль Долг, который отнимают от нуля, становится имуществом, а имущество- долгом. Если нужно отнять имущество от долга, а долг от имущества, то берут их сумму» Отрицательными числами индийские математики пользовались при решении уравнений, причем, вычитание заменяли добавлением с равнопротивоположным числом. Вместе с отрицательными числами индийские математики ввели понятие ноль, что позволило им создать десятеричную систему исчисления. Долгое время ноль не признавали числом, например, «nullus» по-латыни — «никакой, отсутствие числа». Лишь через десять веков, в XVII-ом столетии с введением системы координат ноль становится числом.

В Европе к идее отрицательного количества достаточно близко подошел в начале XIII столетия Леонардо Пизанский, однако в явном виде отрицательные числа применил впервые в конце XV столетия французский математик Шюке. Современное обозначение положительных и отрицательных чисел со знаками « +» и « –» применил немецкий математик Видман, однако еще в ХVI столетии много математиков даже, например, Виет, не признавали отрицательных чисел.

Натуральные числа, противоположные им отрицательные числа и ноль называются «целыми» числами. Целые и дробные числа на втором уровне обобщения получили общее название — рациональные числа. Их называли также «относительными», потому что любое из них можно представить отношением двух целых чисел. Каждое рациональное число можно представить как бесконечную периодическую десятичную дробь. С помощью рациональных чисел можно осуществлять различные измерения, например, длины отрезка при выбранной единице масштаба, с любой точностью. То есть, совокупность рациональных чисел достаточна для удовлетворения большинства практических потребностей. Несмотря на то, что интуитивная интерпретация отрицательных чисел сама по себе полезна, пытаясь понять такие «правила», как «долг» и «имущество»

или должны определить отрицательные числа с помощью положительных. Для этого нам нужно построить множество таких математических объектов, которые будут вести себя в арифметике и алгебре именно так, как можно было бы ожидать от отрицательных чисел. Один из способов построить такое множество состоит в рассмотрении упорядоченных пар положительных чисел (a,b). «Упорядоченность» означает, что, например, пара (2,3) отлична от пары (3,2). Такие упорядоченные пары можно рассматривать как новый класс чисел. Теперь мы должны сказать, когда два таких новых числа равны и что означает их сложение и умножение. Наш выбор определений обусловлен желанием, чтобы пара (a,b) действовала как разность (a — b), которая пока что определена, лишь когда a больше b. Так как в алгебре (a — b) + (c — d) = (a + c) — (b + d), мы приходим к необходимости определить сложение новых чисел как (a,b) + (c,d) = (a + c, b + d); т.к. (a — b (*) c — d) = ac + bd — (bc + ad), мы определяем умножение равенством (a,b (*) c,d) = (ac + bd, bc + ad); а так как (a — b) = (c — d), если a + d = b + c, мы определяем равенство новых чисел соотношением (a,b) = (c,d), если a + d = b + c. Таким образом, используя определения равенства пар, можно записать сумму и произведение пар в более простом виде. Все пары (a,a) равны, по определению равенства пар, и действуют так, как по нашим ожиданиям (1,1) = 0 должен действовать нуль. Например, (2,3) + (1,1) = (3,4) = (2,3); (2,3) (2 +3, 2 +3) = (5,5) = (1,1).

Пары (a,a) мы можем обозначить символом 0, который до сих пор не использовали. Пары (a,b), где b больше a, ведут себя так, как должны были бы действовать отрицательные числа, и мы можем обозначить пару (a,b) символом — (b — a). Необходимо подчеркнуть, что поскольку пары (a,b), где b меньше a, действуют как положительные целые числа (a — b), мы будем записывать такие числа как (a — b). При этом надо забыть о положительных целых числах, с которых мы начали, и впредь пользоваться только нашими новыми числами, которые назовем целыми числами. То, что мы намереваемся использовать старые названия для некоторых новых чисел, не должно вводить в заблуждение относительно того, что в действительности новые числа представляют собой объекты иного рода.

1.3 Дробные числа

С возникновением представлений о целых числах возникали представления и о частях единицы, точнее, о частях целого конкретного предмета. С появлением натурального числа n возникло представление о дроби вида 1/n, которая называется сейчас «аликвотной», «родовой» или «основной». Чтобы выяснить вопрос о происхождении дроби, надо остановиться не на счете, а на другом процессе, который возник со стародавних времен, на измерении. Исторически дроби возникли в процессе измерения. В основе любого измерения всегда лежит какая-то величина (длина, объем, вес и т.д.). Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей. Так возникали первые конкретные дроби как определенные части каких-то определенных мер. Только гораздо позже названиями этих конкретных дробей начали обозначать такие же самые части других величин, а потом и абстрактные дроби. Дробные числа и действия с ними в древности были «высшей математикой». Первая дробь, с которой познакомились люди, была, наверное, половина. За ней последовали 1/4, 1/8 …, затем 1/3, 1/6 и т.д., то есть самые простые дроби, доли целого, называемые единичными или основными дробями. У них числитель всегда единица. Некоторые народы древности и, в первую очередь, египтяне выражали любую дробь в виде суммы только основных дробей. Лишь значительно позже у греков, затем у индийцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. [7]

В Древнем Египте архитектура достигла высокого развития. Для того, чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику. Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4 000 лет назад имели десятичную, но не позиционную, систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела. Вот как записывали египтяне свои дроби. Если, например, в результате измерения получалось дробное число 3/4, то для египтян оно представлялось в виде суммы единичных дробей 1/2 +1/4. Общего понятия дроби у египтян не было, все неканонические дроби представлялись как сумма аликвотных, так называемых основных, дробей, то есть дробей, имеющих числителем единицу. Типовые разложения были сведены в громоздкие таблицы. Единственное исключение составляла дробь 2/3 = 1– 1/3, для которой существовал специальный иероглиф. Сведение к суммам основных дробей производилось с помощью таблиц, которые давали разложение дробей вида 2/n (единственное необходимое разложение), так как умножение было двоичным. Папирус Райнда дает таблицу, в которой приведены разложения на основные дроби для всех нечетных n от 5 до 331. Например,

2/7=1/4+1/28

2/97=1/56+1/659+1/776

5/7=1/2+1/7+1/14.

Из чего исходили при таком сведении к основным дробям? Не ясно. Например, почему 2/9 заменяется суммой 1/12+1/76+1/144, а не суммой 1/12+1/57+1/228? Такие действия с дробями придавали египетской математике тяжеловесность и растянутость, однако разложение на сумму основных дробей применялось в течение тысячелетий, не только в эпоху эллинизма, но и в средние века. В то же время, указанное разложение предполагает определенное, математическое искусство и существуют интересные теории для объяснения того способа, каким египетские специалисты могли получить свои результаты. Многие задачи очень просты и сводятся к линейному уравнению с одним неизвестным. Например, некое количество, его 2/3 части, его 1/2 часть и его 1/7, сложенные вместе, дают 33. Каково это количество? Ответ:14 +28/97.

Раскопками, проведенными в ХХ веке среди развалин древних городов южной части Двуречья, обнаружено большое количество клинописных математических табличек. Ученые, изучая их, установили, что за 2000 лет до н. э. у вавилонян математика достигла высокого уровня развития. Письменная шестидесятеричная нумерация вавилонян комбинировалась их двух значков: вертикального клина ▼, обозначавшего единицу, и условного знака ◄, обозначавшего десять. В вавилонских клинописных текстах впервые встречается позиционная система счисления. Вертикальный клин обозначал не только 1, но и 60, 602, 603 и т. д. Знака для нуля в позиционной шестидесятеричной системе у вавилонян вначале не было. Позже был введен знак, заменяющий современный ноль, для отделения разрядов между собой. Происхождение шестидесятеричной системы счисления у вавилонян связано, как полагают ученые, с тем, что вавилонская денежная и весовая единицы измерения подразделялись в силу исторических условий на 60 равных частей: 1 талант = 60 мин; 1 мина = 60 шекель. Шестидесятые доли были привычны в жизни вавилонян. Вот почему они пользовались шестидесятеричными дробями, имеющими знаменателем всегда число 60 или его степени: 602 = 3600, 603 = 216000 и т. д. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями. [31]

Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360 градусов, градуса на 60 мин., минуты на 60с. Вавилоняне внесли ценный вклад в развитие астрономии. Шестидесятеричными дробями пользовались в астрономии ученые всех народов до XVII века, называя их астрономическими дробями. В отличие от них, дроби общего вида, которыми пользуемся мы, были названы обыкновенными.

В Древней Греции арифметику — учение об общих свойствах чисел, отделяли от логистики — искусства исчисления. Греки считали, что дроби можно использовать только в логистике. Здесь мы впервые встречаемся с общим понятием дроби вида m/n. Таким образом, можно считать, что впервые область натуральных чисел расширилась до области дополнительных рациональных чисел в Древней Греции не позднее V столетия до н. э. Греки свободно оперировали всеми арифметическими действиями с дробями, но числами их не признавали.

В Древней Греции существовали две системы письменной нумерации: аттическая и ионийская или алфавитная. Они были так названы по древнегреческим областям — Аттика и Иония. В аттической системе, названной также геродиановой, большинство числовых знаков являются первыми буквами греческих соответствующих числительных, например, ГЕNTE (генте или центе) — пять, ΔЕКА (дека) — десять и т. д. Эту систему применяли в Аттике до I века н.э., но в других областях Древней Греции она была еще раньше заменена более удобной алфавитной нумерацией, быстро распространившейся по всей Греции. Греки употребляли наряду с единичными, «египетскими» дробями и общие обыкновенные дроби. Среди разных записей употреблялась и такая: сверху знаменатель, под ним — числитель дроби. Например, 5/3 означало три пятых и т. д.

В Древнем Риме пользовались, в основном, только конкретными дробями, которые заменяли абстрактные части подразделами используемых мер. Они остановили свое внимание на мере «асс», который у римлян служил основной единицей измерения массы, а также денежной единицей. Асс делился на двенадцать частей — унций. Из них складывали все дроби со знаменателем 12, то есть 1/12, 2/12, 3/12… Так возникли римские двенадцатеричные дроби, то есть дроби, у которых знаменателем всегда было число 12. Вместо 1/12 римляне говорили «одна унция», 5/12 — «пять унций» и т. д. Три унции назывались четвертью, четыре унции — третью, шесть унций — половиной. Сейчас «асс» — аптекарский фунт. Слово «процент» происходит от латинских слов procentum, что буквально означает «за сотню» или «со ста». Процентами очень удобно пользоваться на практике, так они выражают части целых чисел в одних и тех же сотых долях. Это дает возможность упрощать расчеты и легко сравнивать части между собой и с целым. Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы.

Ныне процент — это частный вид десятичных дробей, сотая доля целого, принимаемого за единицу. В некоторых вопросах иногда применяют и более мелкие, тысячные доли, так называемые промилле (от латинского promille — «с тысячи»), обозначаемые ‰ по аналогии со знаком процента %. Однако, на практике в большинстве случаев «тысячные» — слишком мелкие доли, десятые же доли слишком крупные. Поэтому больше всего удобны сотые доли, иначе говоря, проценты.

Дроби в Индии записывались вертикально, как делаем и мы, только вместо черты дроби их заключали в рамку, так же, как в Китае и у поздних греков. Действия с дробями ничем не отличались от современных. У индийского математика Брахмагупты находим достаточно развитую систему дробей. У него встречаются разные дроби и основные, и производные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим.

В китайской «Математике в девяти разделах» уже имеют место сокращения дробей и все действия с дробями. Дроби у китайцев появились почти одновременно с целыми числами, задолго до «отрицательных» чисел. В китайских правилах, операций с дробями для современного человека нет ничего необычного, но именно это и нетривиально, так как дроби в истории арифметики многих народов долгое время считались одним из самых запутанных разделов. Ко второму веку до нашей эры китайским математикам удалось достаточно полно разработать все операции с дробями. Математики того времени могли не только с помощью алгоритма Евклида, но в число арифметической форме, отыскивался наибольший общий делитель числителя и знаменателя, необходимый для сокращения дроби. Сложение и вычитание представлено общими правилами, отличающимися от современных лишь незначительно: вместо наименьшего общего кратного знаменателей берется просто их произведение. [26]

Арабы первыми начали отделять чертой числитель от знаменателя. Леонардо Пизанский, перенявший знания у арабов, записывает дроби, помещая в случае смешанного числа, целое число справа, но читает так, как принято у нас. Иордан Неморарий (XIII в.) выполняет деление дробей с помощью деления числителя на числитель и знаменателя на знаменатель, уподобляя деление умножению. Для этого приходится члены первой дроби дополнять множителями. Как свидетельствуют памятники русской истории, славяне, находившиеся в культурном общении с Византией, пользовались десятичной алфавитной славянской нумерацией, сходной с ионийской. Над буквами-числами ставился особый знак, названный «титло». Для обозначения тысячи применялся другой знак, который приставлялся слева от букв.

В русских рукописных арифметиках XVII века дроби называли долями, позднее «ломаными числами». В старых руководствах находим следующие названия дробей на Руси: 1/2 — половина, полтин; 1/3 — треть;1/4 — четь;1/6 — полтреть; 1/8 — полчеть; 1/12 –полполтреть; 1/16 — полполчеть; 1/24 — полполполтреть (малая треть); 1/32 — полполполчеть (малая четь); 1/5 — пятина;1/7 — седьмин;1/10 — десятина. Славянская нумерация употреблялась в России до XVI века, затем в страну начала проникать десятичная позиционная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I. В XV — XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках. Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало — зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.

Рассмотрим вопрос о возникновении десятичных дробей. Со временем практика измерений и вычислений показала, что проще и удобнее пользоваться такими мерами, у которых отношение двух ближайших единиц длины было бы постоянным и равнялось бы именно десяти — основанию нумерации. Этим требованиям отвечает метрическая система мер. Она возникла во Франции как одно из следствий буржуазной революции. Новые меры должны были удовлетворять следующим требованиям: основой общей системы мер должна быть единица длины; меры длины, площади, объема, вместимости и веса должны быть связаны между собой; основную меру длины следовало выбрать так, чтобы она была постоянной «для всех времен и всех народов»; основанием системы мер необходимо было взять число, равное основанию системы счисления. [8]

Во Франции за основную меру длины приняли одну десятимиллионную часть четверти земного меридиана и назвали ее метром, от греческого слова «метрон», означающего «мера». На основании измерений меридиана, сделанных французскими учеными Мешеном и Даламбером, был изготовлен впоследствии платиновый эталон метра. Число 10 легло в основу подразделений метра. Вот почему метрическая система мер, применяемая ныне в большинстве стран мира, оказалась тесно связанной с десятичной системой счисления и с десятичными дробями. Однако следует отметить, что европейцы не первые, кто пришел к необходимости использовать десятичные дроби в математике. Зарождение и развитие десятичных дробей в некоторых странах Азии было тесно связано с метрологией, учением о мерах. Уже во II веке до н.э. там существовала десятичная система мер длины на Востоке. Примерно в III веке н.э. десятичный счет распространился на меры массы и объема. Тогда и было создано понятие о десятичной дроби, сохранившей, однако метрологическую форму. Например, в Китае в Х веке существовали следующие меры массы: 1 лан = 10 цянь = 102 фэнь = 103 ли = 104 хао = 105 сы = 106 хо. Если вначале десятичные дроби выступали в качестве метрологических, конкретных дробей, то есть десятых, сотых и т. д. частей более крупных мер, то позже они по существу стали все более приобретать характер отвлеченных десятичных дробей. Целую часть стали отделять от дробной особым иероглифом «дянь» (точка). Однако в Китае как в древние, так и в средние века десятичные дроби не имели полной самостоятельности, оставаясь в той или иной мере связанными с метрологией. Более полную и систематическую трактовку получают десятичные дроби в трудах среднеазиатского ученого ал-Каши в XV веке. Независимо от него, в 80-тых годах XVI века десятичные дроби были «открыты» заново в Европе нидерландским математиком Стевином. С начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. В Англии в качестве знака, отделяющего целую часть от дробной, была введена точка. Запятая, как и точка, в качестве разделительного знака была предложена в 1617 году математиком Непером. Развитие промышленности и торговли, науки и техники требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в сельском хозяйстве и промышленности десятичные дроби и их частный вид — проценты применяются намного чаще, чем обыкновенные дроби.

Интуитивно мы представляем себе дробь 2/3 как результат разбиения 1 на три равные части и взятия двух из них. Однако, математик стремится как можно меньше полагаться на интуицию и определять рациональные числа через более простые объекты — целые числа. Это можно сделать, если 2/3 рассматривать как упорядоченную пару (2,3) целых чисел. Для завершения определения необходимо сформулировать правила равенства дробей, а также сложения и умножения. Разумеется, эти правила должны быть эквивалентны правилам арифметики и, естественно, отличаться от правил для тех упорядоченных пар, которые мы определили как целые числа. Вот эти правила:

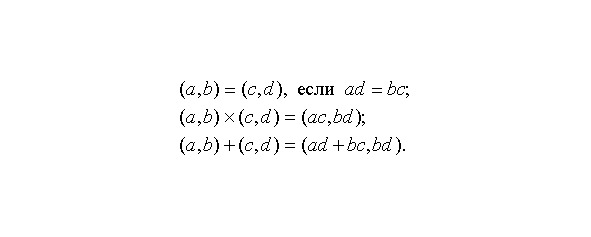
Нетрудно видеть, что пары (a,1) действуют как целые числа a; продолжая рассуждать так же, как в случае отрицательных чисел, мы обозначим через 2 дробь (2,1), или (4,2), или любую другую дробь, равную (2,1). Забудем теперь о целых числах, сохраним их лишь как средство записи определенных дробей. Знакомым примером такого обобщения является возникновение понятий рациональных, действительных и комплексных чисел. Все эти понятия можно рассматривать как последовательные обобщения натурального числа. Поскольку обобщения происходят обычно в рамках определенных теорий, то с равным основанием можно говорить такие обобщения математических теорий. При этом, во-первых, происходит расширение области применения новой обобщенной теории, а во- вторых, сохраняется связь преемственность между новой и старой теорией. Дроби принято также называть рациональными числами, так как они представимы в виде отношений (от лат. ratio — отношение) двух целых чисел, но если нам потребуется число, квадрат которого равен 2, то мы не сможем обойтись рациональными числами, т.к. не существует рационального числа, квадрат которого равен 2. То же самое выяснится, если поинтересоваться числом, выражающим отношение длины окружности к ее диаметру. Следовательно, если мы хотим получить квадратные корни из всех положительных чисел, то нам необходимо расширить класс рациональных чисел. Новые числа, называемые иррациональными (т.е. не рациональными), можно определять различными способами. Упорядоченные пары для этого не годятся; один из простейших способов состоит в том, чтобы определить иррациональные числа как бесконечные непериодические десятичные дроби. Таким образом, исторически первым расширением понятия о числе является присоединение к множеству натуральных чисел множества всех дробных чисел.

1.4 Иррациональные и комплексные числа

Еще в Древнем Египте и Вавилоне были известны так называемые «несоизмеримые» отрезки, которые нельзя было выразить отношением через рациональные числа. Точно неизвестно, исследование каких вопросов привело к открытию несоизмеримости. Это могло произойти: в геометрических расчетах при нахождении общей меры стороны и диагонали квадрата; в теории музыки при попытках поделить октаву пополам, что сводится к определению среднего геометрического между 1 и 2; в арифметике при определении дроби, квадрат которой равняется двум. Открытие факта, что между двумя отрезками стороной и диагональю квадрата не существует общей меры, привело к настоящему кризису основ, по крайней мере, в древнегреческой математике. Факт существования несоизмеримых отрезков, тем не менее, не тормозил развитие геометрии в древней Греции. Греки разработали теорию отношения отрезков, которая учитывала возможность их несоизмеримости. Они умели сравнивать такие соотношения по величине, выполнять над ними арифметические действия в чисто геометрической форме, иначе говоря, пользоваться такими соотношениями как числами, что привело к понятию иррационального числа. [26]

Индийцы рассматривали иррациональные числа, как числа нового вида, но допускающие над ними такие же арифметические действия, как и над рациональными числами. Например, индийский математик Бхаскара уничтожает иррациональность в знаменателе, умножая числитель и знаменатель на тот же самый иррациональный множитель. Развивая тригонометрию как самостоятельную научную дисциплину, азербайджанский ученый XIII столетия Насретдин ат-Туси (1201- 1274 гг.) трактует соотношение несоизмеримых величин как числа: «Каждое из этих соотношений может быть названо числом, которое измеряется единицей так же само, как один из членов соотношения обозначается другим из этих членов». Похожую трактовку числа давал и Омар Хайям.

Древние математики, изучая отношения между геометрическими и числовыми величинами, столкнулись с иррациональными числами, Эти числа они назвали трансцендентными. К таким числам и относится число π. В Древней Индии встречается значение, т.е. 3,162…Китайский Астроном Ван Фань (229—267гг. н.э.) утверждал, что, т.е. 3,155…, а Цзу Чун-Джи (428—499гг.) говорил о «неточном» значении и о «точном», показав, что содержится между 3,1415926 и 3,1415927.В индийских сутрах (VII–Vвв. до н.э.) имеются правила, из которых вытекает, что. Арибхатта и Бхаскара брали значение, т.е. 3,1416….В своей книге «Об измерении окружности» (1424г.) аль-Каши нашел для значение, далеко превосходящее по точности все ранее известные. Рассмотрев вписанный и описанный многоугольники с 800 335 168 сторонами, он получает окончательный результат, выраженный в шестидесятиричных и в десятиричных дробях в виде, т.е. — 16 верных знаков. Если обозначить радиус круга через, то речь будет идти о построении круга, площадь которого равна, а сторона равна. Теперь известно, что число — отношение длины окружности к своему диаметру — число иррациональное, которое выражается бесконечной десятичной дробью 3,141592… Первое строгое доказательство иррациональности этого числа было дано на основе работы И. Г. Ламберта в 1766г. математиком А. М. Лежандром. Это доказательство, тем не менее, не исключает возможности квадратуры круга, так как известны иррациональные числа, которые могут быть построены с помощью циркуля и линейки (). Затем немецкий математик Ф. Линдеман, опираясь на исследования Ш. Эрмита, в 1882г. нашел строгое доказательство того, что число не только иррационально, но не может быть корнем алгебраического уравнения. Из этого следует, что с помощью только циркуля и линейки построить отрезок, равный длине окружности, невозможно. [27]

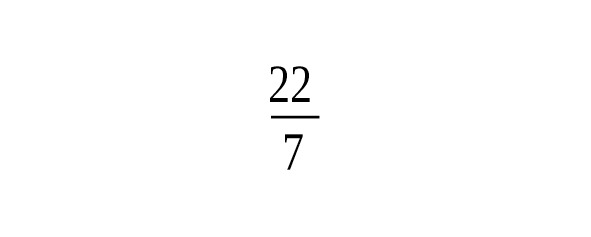
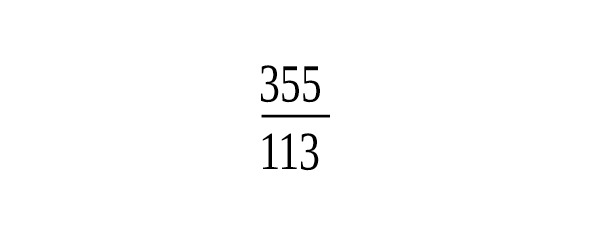
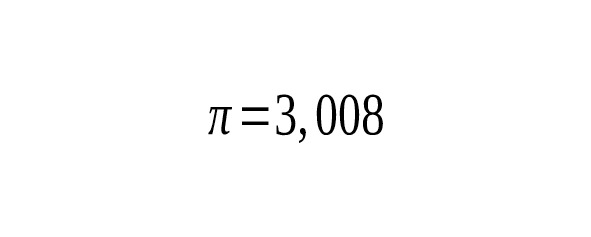
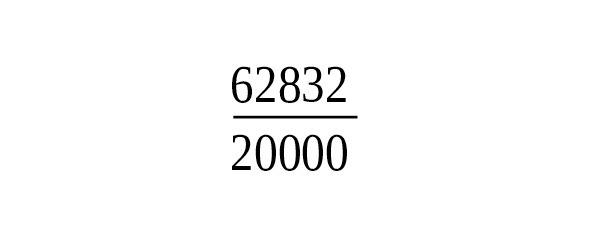
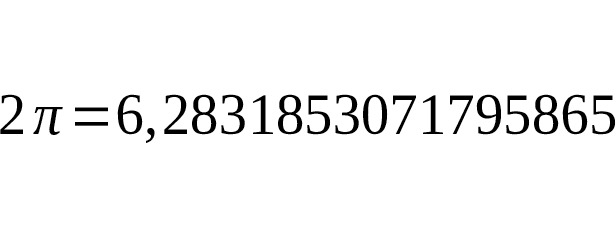
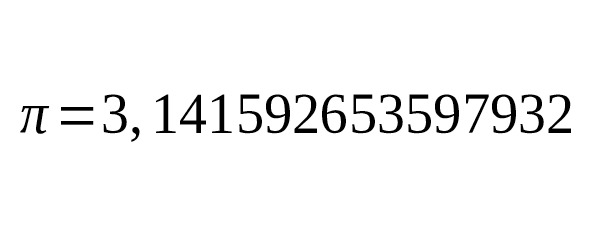
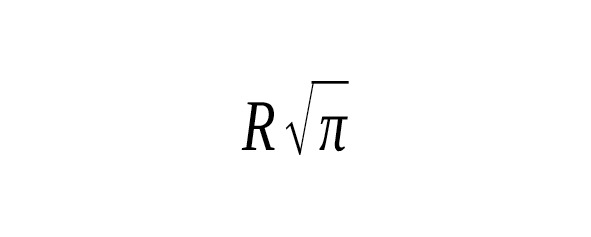
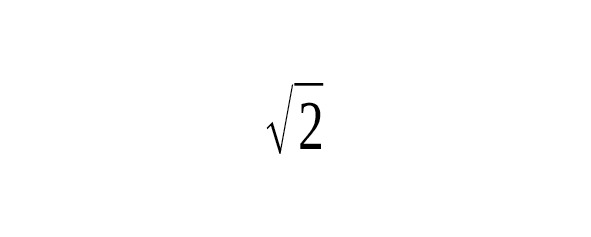
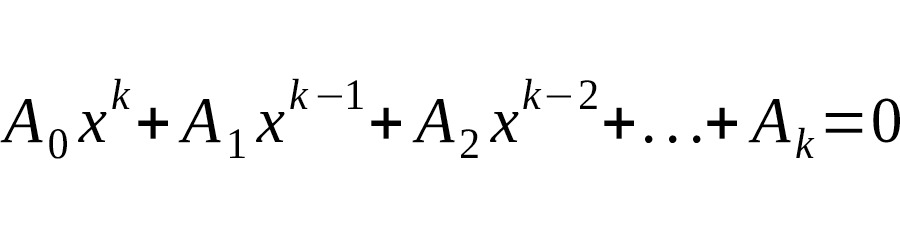
Первым ввел обозначение отношения длины окружности к диаметру современным символом английский математик У. Джонсон в 1706 году. В качестве символа он взял первую букву греческого слова «периферия», что в переводе означает «окружность». Введенное обозначение стало общеупотребительным после опубликования работ Л. Эйлера в 1736 году. Число определяется аналитически. В современной математике число — не только отношение длины окружности к диаметру, но и элемент различных формул, в том числе формулы неевклидовой геометрии и знаменитой формулы Л. Эйлера. Последняя устанавливает связь числа и числа е следующим образом (см. ниже). Эта и другие взаимосвязи позволили математикам еще глубже выяснить природу числа.

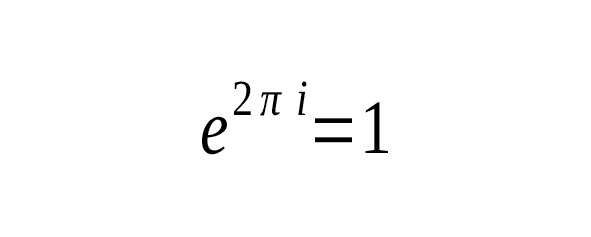
Рациональные и иррациональные числа вместе называются действительными или вещественными числами. Геометрически их можно представить точками на прямой, при этом дроби оказываются в промежутках между целыми числами, а иррациональные числа — в промежутках между дробями, Выделим характерные особенности рассмотренных (натуральных, рациональных, действительных) чисел: они моделируют только одно свойство — количество; они одномерны и все изображаются точками на одной прямой, называемой координатной осью, то есть можно показать что система действительных чисел обладает свойством, известным как «полнота» и означающим, что каждой точке на прямой соответствует некоторое действительное число. Действительные числа иногда подразделяют также на алгебраические и трансцендентные. Алгебраическими называют числа, которые являются корнями алгебраических многочленов с целыми коэффициентами. Все остальные (неалгебраические) числа относятся к трансцендентным. Так как каждое рациональное число является корнем соответствующего многочлена первой степени с целыми коэффициентами, то все трансцендентные числа иррациональны.

В Европе существование геометрических несоизмеримых величин в средние века не оспаривалось, но для многих иррациональные числа были лишь символами, лишенными точно определенного содержания, поэтому их называли «глухими», «недействительными», «фиктивными» и т. д. Только после появления геометрии Декарта в 1637 году началось применение иррациональных, как впрочем, и отрицательных чисел. Идеи Декарта привели к обобщению понятия о числе. Между точками прямой и числами было определено взаимно однозначное соответствие. В математику была введена переменная величина.

Итак, в начале XVIII столетия существовало три понятия иррационального числа: иррациональное число рассматривали как корень n-ой степени из целого или дробного числа, когда результат извлечения корня нельзя выразить «точно» целым или дробным числом; иррациональное число трактовали как границу, к которой его рациональные приближения могут подойти как угодно близко; число рассматривали как отношение одной величины к другой величине того же самого рода, взятой за единицу; когда величина несоизмерима с единицей, число называли иррациональным. Позднее Эйлер, Ламберт показали, что иррациональные числа можно представить бесконечными непериодическими десятичными дробями, например, π=3,141592….

Свое дальнейшее развитие теория иррациональных чисел получила во второй половине XIX века в трудах Дедекинда, Кантора и Вейерштрасса в связи с потребностями математического анализа. Таким образом рациональные и иррациональные числа на третьем уровне обобщения образовали действительные числа. [30]

Более странными, чем иррациональные, оказались числа новой природы, открытые итальянским ученым Кардано в 1545 году. Он показал, что система уравнений, не имеющая решений во множестве действительных чисел, имеет решение. Нужно только условиться действовать над такими выражениями по правилам обычной алгебры. Кардано называл такие величины «чисто отрицательными» и даже «софистически отрицательными», считал их бесполезными и старался не употреблять. Долгое время эти числа считали невозможными, несуществующими, воображаемыми. Декарт назвал их «мнимыми», Лейбниц — «уродом из мира идей, сущностью, находящейся между бытием и небытием». Казалось бы, что с помощью таких чисел нельзя выразить ни результат измерения какой-нибудь величины, ни изменение какой-нибудь величины. Мнимым числам не было места на координатной оси. Однако ученые заметили, что если взять действительное число b на положительной части координатной оси и умножить его на i, то получим мнимое число b i, неизвестно где расположенное. Если это число еще раз умножить на i, то получим –b, то есть первоначальное число, но уже на отрицательной части координатной оси. Итак, двумя умножениями на i мы перебросили число b с положительного в отрицательные, и ровно на середине этого броска число было мнимым. Так нашли место мнимым числам в точках на мнимой координатной оси, перпендикулярной к середине действительной координатной оси. Точки плоскости между мнимой и действительной осями изображают числа, найденные Кардано, которые в общем виде a + b·i содержат действительные числа а и мнимые b·i в одном комплексе (составе), поэтому называются комплексными числами. Было дано геометрическое истолкование комплексных чисел. Около 1800-го года сразу несколько математиков (Вессель, Арган, Гаусс) поняли, что комплексными числами можно моделировать векторные величины на плоскости. Если действительные числа (состоящие из одного элемента) одномерны — они размещаются на одной координатной оси. Комплексные числа состоят из двух элементов, для их представления необходима уже плоскость и две координатные оси. Это значит, что они двумерны.

Оказалось, что комплексное число z = a + b · i можно изобразить точкой М (a,b) на координатной плоскости. Позднее выяснили, что удобнее всего изображать число не самой точкой М, а в виде вектора, идущего из начала координат в точку с координатами а и b.

Вектор можно задавать не только его координатами a и b, но также длиной r и углом φ, который он образует с положительным направлением оси абсцисс.

a = r · cos φ, b = r · sin φ

z = r · (cos φ + i · sin φ)

При этом формула называется тригонометрической формой комплексного числа. Число r называют модулем комплексного числа z. Число φ называют аргументом z и обозначают ArgZ. Заметим, что если z = 0, значение ArgZ не определено, а при z ≠ 0 оно определено с точностью до кратного 2π. Упомянутая ранее формула Эйлера позволяет записать число z в виде показательной форме.

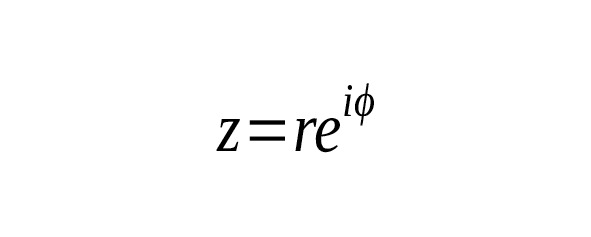
Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного, расширило область их применения. Так как квадраты положительных и отрицательных действительных чисел положительны, на прямой действительных чисел нет точки, соответствующей числу, квадрат которого был бы равен –1. Если бы мы попытались решать квадратные уравнения типа x2 +1 = 0, то необходимо было бы поступать так, как если бы существовало некоторое число i, квадрат которого был бы равен –1. Поскольку такого числа нет, нам не остается ничего другого, как воспользоваться «воображаемым», или «мнимым», числом. Соответственно, «число» i и его комбинации с обычными числами (типа 2 +3i) стали называться мнимыми. [29]

Современные математики предпочитают называть такие числа «комплексными», поскольку они, как мы увидим, столь же «реальны», как и те, с которыми нам уже доводилось встречаться раньше. Долгое время математики свободно пользовались мнимыми числами и получали полезные результаты, хотя не до конца понимали то, что они делали. До начала 19 века никому и в голову не приходило «оживить» мнимые числа с помощью их явного определения. Для этого нужно построить некоторую совокупность математических объектов, которые с точки зрения алгебры вели бы себя как выражения a + bi, если условиться, что i 2 = –1. Такие объекты можно определить следующим образом. Рассмотрим в качестве наших новых чисел упорядоченные пары действительных чисел, сложение и умножение которых определяется формулами:

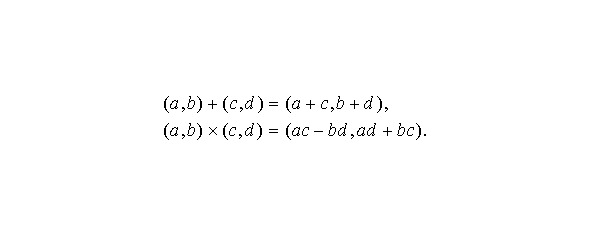
Назовем такие упорядоченные пары комплексными числами. Пары частного вида (a,0) со вторым членом, равным нулю, ведут себя как действительные числа, поэтому мы условимся обозначать их так же: например, 2 означает (2,0). С другой стороны, комплексное число (0,b) по определению умножения обладает свойством (0,b (0, 0) b) = (0 — b2, 0 +0) = (–b2,0) = –b2. (0,1) мы находим произведение (–1,0). Например, в случае (0,1) (0,1) 2 = (–1,0). Мы уже условились записывать комплексное число (–1,0) как –1, поэтому если число (0,1) обозначить символом i, то мы получим комплексное число i, такое, что i 2 = –1. Кроме того, комплексное число (2,3) теперь можно записать в виде 2 +3i. Важное отличие такого подхода к комплексным числам от традиционного состоит в том, что в данном случае число i не содержит ничего загадочного или мнимого: оно представляет собой нечто, хорошо определяемое посредством уже существовавших ранее чисел, хотя, разумеется, и не совпадает ни с одним из них. Точно так же, действительное число 2 не является комплексным, хотя мы и используем символ 2 для обозначения комплексного числа. Так как на самом деле в мнимых числах нет ничего «мнимого», то неудивительно, что они широко используются в реальных ситуациях, например в электротехнике (где вместо буквы i обычно используют букву j, так как в электротехнике i — символ для текущего значения силы тока).Алгебра комплексных чисел во многом напоминает алгебру действительных чисел, хотя имеются и существенные различия. Например, правило для комплексных чисел не выполняется:, поэтому, в то время как

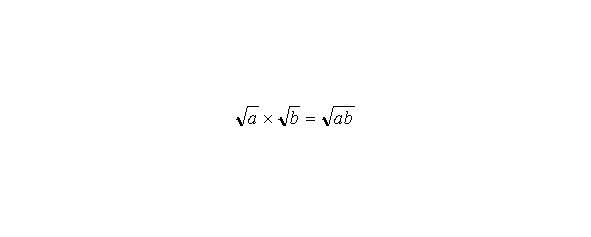
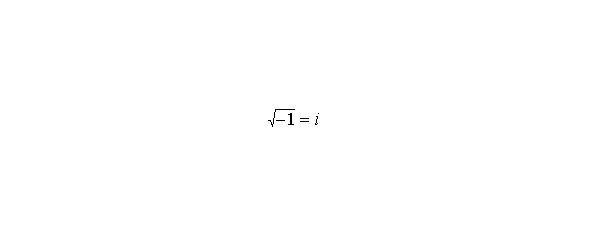
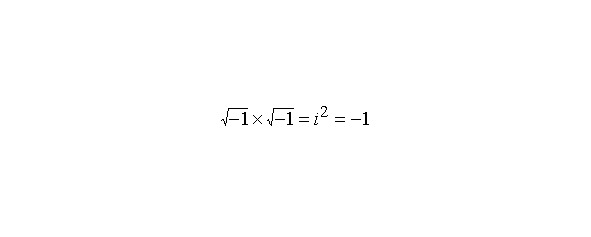
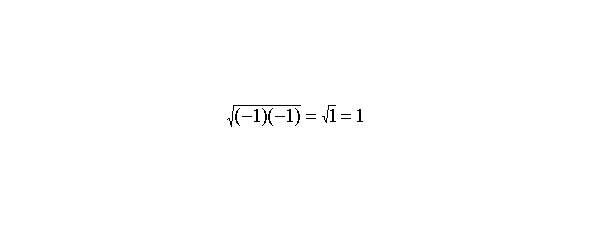
Определение комплексных чисел как пар действительных чисел подсказывает способ их наглядного геометрического представления. Хотя прямая не может вместить и действительные, и комплексные числа, их вполне может вместить плоскость. Сложение комплексных чисел допускает простую геометрическую интерпретацию. Например, сумма чисел 2 +3i и 3 — i есть число 5 +2i, которому соответствует четвертая вершина параллелограмма с тремя вершинами в точках 2+3i и 3–i.

Точку на плоскости можно задавать не только прямоугольными (декартовыми) координатами (x,y), но и ее полярными координатами (r,х), задающими расстояние от точки до начала координат и угол. Следовательно, комплексное число x + iy может быть записано и в полярных координатах. Длина радиус-вектора r равна расстоянию от начала координат до точки, соответствующей комплексному числу; величина r называется модулем комплексного числа и определяется по формуле. Часто модуль записывают в виде

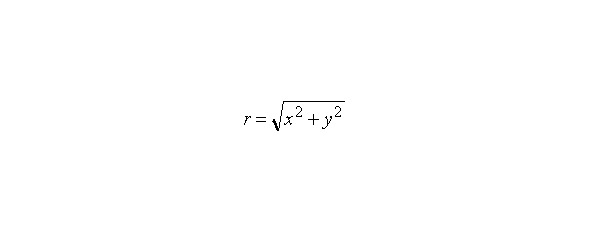
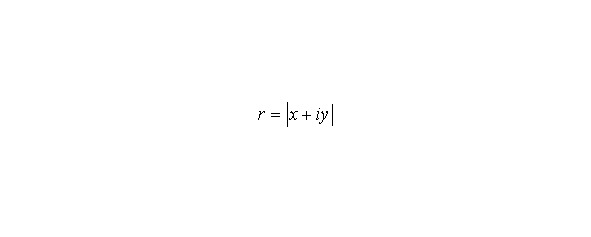
Угол называется «углом», «аргументом» или «фазой» комплексного числа. Такое число имеет бесконечно много углов, отличающихся на величину, кратную 360°. В полярных координатах справедливо равенство

x = r cos х, y = r sin х

x + iy = r (cos х + i sin х).

Если z = x + iy, то число x — iy называется комплексно сопряженным с z и обозначается, а в технике z*. Формула удобна для вычисления модуля комплексного числа z, особенно если это число определяется сложной формулой. Пользуясь формулами тригонометрии, находим:

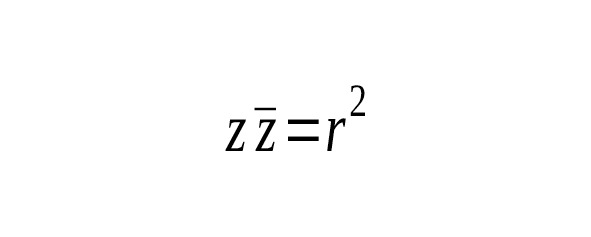
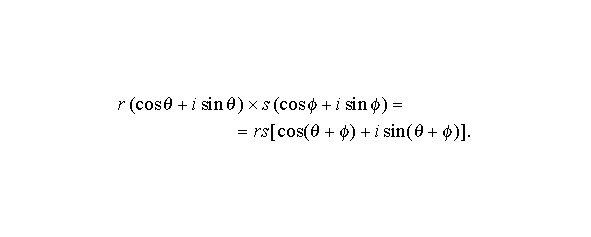
Отсюда правило: чтобы перемножить два комплексных числа, необходимо умножить их модули и сложить их аргументы, более общая, n-я степень того же числа равна rn (cos хn + i sin хn) (формула Муавра). Эта формула справедлива при надлежащей интерпретации, даже если n — не положительное целое число. Например,

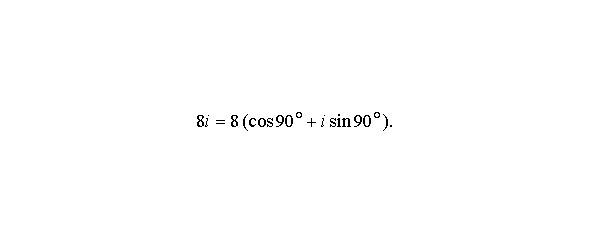
Следовательно, можно ожидать, что кубический корень из 8i (n = 1/3) будет равен

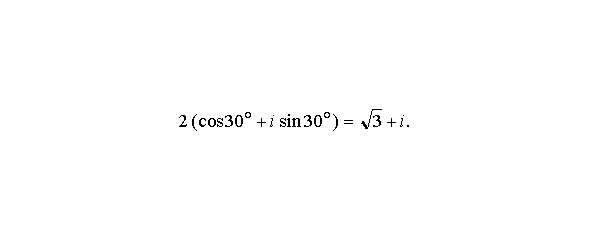
Поскольку аргумент числа i можно считать равным и 90°+360°= 450°, и 90°+360°+360°= 810°, мы можем найти еще два кубических корня из 8i, а именно: