Бесплатный фрагмент - Исследование и оценка параметров сигналов в распределенных информационных системах

Физика информации

Имеются различные понятия определения информации. Есть философские понятия информации, определение информации в широком смысле как понимают люди, в узком научном смысле какой ему придал Шеннон и другие подходы.

ГОСТ Р 50922—96 определяет информацию как сведения о лицах, предметах, фактах, событиях, явлениях и процессах независимо от формы их представления

Рассмотрим физическую модель информации. Введем понятие информация — физическое поле.

Физическим полем называется область пространства, где проявляют себя физические, достоверно зарегистрированные и точно измеренные силы. В рамках современной физики известны и изучены четыре вида материальных полей: гравитационное, электромагнитное — магнитное и/или электрическое, поля сильных взаимодействий — ядерное, слабых взаимодействий (Рис.1).

Имеются силовые поля в веществе и в средах, которые проявляются только при наличии материальной среды. К таким полям относятся: акустические, вибрационные, гидроакустические поля и др. Эти поля отсутствуют, если будет отсутствовать среда. Они характеризуются давлением, скоростью, ускорением и другими характеристиками.

Рассмотрим ряд элементарных примеров для понятия «информация — это поле».

Человек видит окружающий мир это отражение от объектов в видимом спектре электромагнитного поля. Восприятие или создание звука это акустическое поле. Электрический ток — движение заряженных частиц под действием электрического или электромагнитного поля. Передача и прием сообщений по каналам связи обеспечивается в различных частотных диапазонах электромагнитного поля.

Образец вооружения и военной техники. Пока он закрыт полностью — нет информации. Движение, работа, функционирование узлов, агрегатов все это создает физические поля, значит, есть информация.

Перемещение материальных частиц и тел, их информационное взаимодействие происходит в поле тяготении, в гравитационном поле.

Процессы в микромире происходят в полях сильных и слабых взаимодействий. Ряд примеров легко продолжить, но на каком конкретном случае мы бы ни остановились, принципы и идеи определяющие, раскрывающие физические процессы создания информации и ее отображения, везде оказываются одинаковыми — это физическое поле. Следовательно, физическое поле как и информация, существует независимо от того воспринимается или регистрируется кем то или чем то.

Физическое поле это особый вид материи. Материя — объективная реальность, данная нам в ощущениях. Считается, что материя существует либо в виде вещества, либо в виде поля.

Основное отличие поля от тел или частиц заключается в том, что оно локализовано в пространстве. Для описания состояния частицы требуется задать ограниченное число параметров равное числу степеней свободы. (Для материальной точки это радиус-вектор r, задаваемый тремя проекциями на оси координат).

Чтобы знать параметры поля в любой точке пространства нужно задать закон, по которому меняется поле в пространстве и начальные параметры. Поле проявляется в силовом воздействии на тела или частицы (действует сила F). Одной из важных количественных характеристик поля, является напряженность. Напряженность поля определяется как отношение силы, действующей на тело, к величине той количественной характеристики, которая участвует в создании поля и определяется полем, поэтому напряженность называют силовой характеристикой поля. Существенно, что напряженность поля является векторной величиной, так же как и сила, через которую она определяется. Таким образом, поле задано, если в каждой точке пространства известна его напряженность.

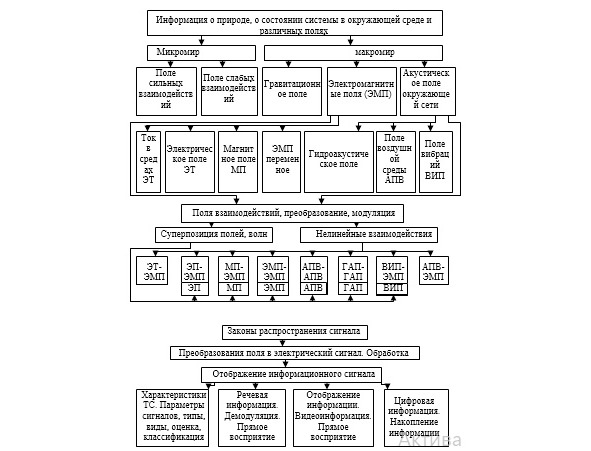
Создание, формирование поля, его распространение, регистрация, прием, измерение характеристик поля и преобразованного поля в электрический сигнал для отображения информации — этот физическая суть создании и получение информации.

Если использовать конструктивный подход к понятию информации и рассматривать понятие «информация» как объект защиты, то этот объект будет описываться меньшим числом факторов, свойств, признаков.

Поэтому целесообразно информацию представить в виде многообразия физических полей, которые отражают среду переноса проявления источников информации, но не сущность информации.

Физические поля (информация) формируются, создаются природой, техническими системами, средствами (ТС), биологическими объектами.

Технические средства имеют так называемые техногенные физические поля. Эти поля несут данные, сведения, как о самом техническом средстве, так и о содержание сведений, которые циркулирует в техническом средстве (например, речевое сообщение в средствах связи, сведения в видеосистемах, в ЭВМ и др.)

Информация — это не только физическое поле определенного вида, но это и так называемые поля взаимодействия электромагнитных полей, поля взаимодействия электромагнитных и акустических полей. При этом наблюдается два вида взаимодействий суперпозиция полей, волн и нелинейные взаимодействия (Рис.1).

Принцип суперпозиции. В общем случае, принцип суперпозиции — это допущение, согласно которому результирующий эффект сложного процесса воздействия эквивалентен сумме эффектов от каждого воздействия в отдельности. Разумеется, это определение предполагает, что эффекты не влияют друг на друга.

Сформулированный принцип справедлив, если система описывается линейными уравнениями. Слабое гравитационное поле с хорошей точностью подчиняется принципу суперпозиции. Для ряда случая электромагнитных полей принцип суперпозиции применим к системе, описываемой нелинейными уравнениями, т.е. меняющейся под действием внешних эффектов, принцип суперпозиции неприменим. Примером нарушения принципа суперпозиции может служить магнитное поле в ферромагнетике. Другой пример — свет (сильное световое поле) в среде. Такое поле может генерировать в среде за счет нелинейного взаимодействия с ней свет на длине волны в два, три или более раз меньшей.

Сильное гравитационное поле не подчиняется принципу суперпозиции, поскольку оно описывается нелинейными уравнениями Эйнштейна. Разделы физики, которые изучают явления, в которых нарушается принцип суперпозиции, обычно называют нелинейными. Например, нелинейная оптика.

В математической модели будут рассмотрены слабые гравитационные, электромагнитные, акустические поля, к которым принцип суперпозиции применим. В дальнейшем рассмотрим суперпозицию, и взаимодействия таких полей: электромагнитного поля (ЭМП), электрического поля (ЭП), магнитного поля (МП), гидроакустического поля (ГАП), акустического поля (АПВ), вибрационного поля (ВП). Примером такого взаимодействия может являться любое излучение акустическое или электромагнитное, в реальных условиях распространения при отражениях.

Нелинейные взаимодействия

Рассмотрим, приведем ряд примеров описание преобразований составляющих ЭМП с ЭМП при наличии нелинейных элементов или структур. Кроме того, будем рассматривать взаимодействие акустического и вибрационного полей с электромагнитным полем на нелинейных элементах и нелинейных средах. Обратимся к рисунку 1.

ЭТ-ЭМП. Классическим примером такого взаимодействия является модуляция электрическим током излучения переменного электромагнитного поля. Это передающие средства связи, телекоммуникаций, радиолокации, телевидения и т. д.

ЭП-ЭМП, МП-ЭМП, Составляющая ЭМП — электрическое поле (ЭП) и магнитное поле (МП) воздействует на радиотехнические цепи радиопередающих устройств, где путем наводки или воздействия на нелинейные элементы транспонируются в другой частотный диапазон. Кроме того, наводятся на линии связи, электропитания и коммуникаций.

ЭМП-ЭМП. Наиболее объемное взаимодействие полей на нелинейных структурах. Охватывает широкий частотный диапазон электромагнитных волн. Воздействие на электрические цепи аналогично ЭП и МП, только защита от такого воздействия сложна. Сведения, которые находятся в таких сформированных полях, иногда очень объемные и не всегда дешифруется. Например, излучение от биологической структуры человека [1].

АПВ-ЭМП. Информационное акустическое поле преобразуется в электрический сигнал, который прямо или после последующих преобразований формируется в электромагнитном поле. Например, акустоэлектрическое преобразование на поверхности.

ВП-ЭМП. Вибрационные колебания модулируют высокочастотные электромагнитные колебания на отражающихся поверхностях. Информация передается электромагнитным полем.

ГАП-ГАП. За счет нелинейности жидкой среды формируются поля и спектры частот, которые содержат сведения о технических средствах. Например, кавитационный спектр, модуляционный спектр и др.

АПВ-АПВ. Формирование и снятие данных за счет взаимодействия акустических волн низких и высоких частот на нелинейных структурах.

Математическая модель физических полей макромира

Математическая модель охватывает класс неопределяемых абстрактных, символических математических объектов, таких как числа или векторы, и отношения между этими объектами.

Под математической моделью понимают количественную формализацию абстрактных представлений об изучаемой системе. Математическая модель это формальное описание системы с помощью математических средств, дифференциальных, интегральных, разностных, алгебраических уравнений, а также неравенств, множеств и т. д.

Рассмотрим математическую модель физических полей макромира (гравитационного, электромагнитного, акустического) (Рис.1), которая характеризует информацию.

Математическая модель гравитационного поля

Математическую модель гравитационного поля представим дифференциальным уравнением гравитационного поля в ньютоновской механике [2].Такое уравнение получаются переходом от закона всемирного тяготения Ньютона, где сила взаимного притяжения двух тел, которые могут быть приняты за материальные точки, прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними, к дифференциальным уравнениям в теории ньютоновского потенциала.

Итак, имеются две материальные точки с массами m и m они притягиваются друг к другу по закону Ньютона и на точку m со стороны точки m действует сила (1.1), где rk — расстояние между точками т и mk, γ — гравитационная постоянная, r — единичный вектор направления от m к m.

Потенциальный характер сил тяготения т. е. Fk = grad Φk, позволяет ввести скалярную характеристику гравитационного поля — потенциал, который для двух материальных точек (1.2).

Если и пространстве имеется n материальных точек с массами m (k = 1, 2,.. п) и рассматривается их влияние на одну материальную точку массы m = 1, которая может быть помещена в разные точки пространства (пробная масса), то со стороны всех точек mk на пробную массу m = 1 будет действовать сила F = ΣFk и ее потенциал (1.3).

Распределение масс mk создает в пространстве гравитационное поле с потенциалом Φ, которое можно обнаружить с помощью пробной массы, помещенной в рассматриваемую точку пространства. Напишем дифференциальное уравнение, которому должен удовлетворять потенциал сил тяготения Φ. [2] Рассмотрим функцию 1 /, где (1.4) — расстояние между точкой х, у, z, в которой помещена пробная масса, и точкой xk, yk, zк, в которой находится k-тая масса, создающая гравитационное поле, является гармонической функцией. Во всех точках х, у, z, для которых rk, функция 1/rk удовлет­воряет уравнению Лапласа (1.5).

Следовательно, потенциал Φk гравитационного поля одной ма­териальной точки удовлетворяет уравнению (1.6).

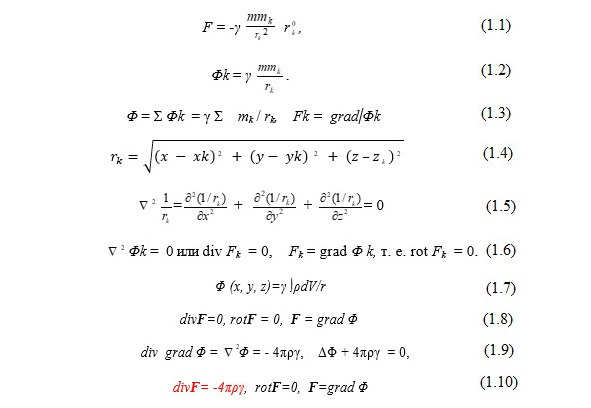
Уравнение Лапласа является линейным уравнением. Потенциал гравитационного поля Φ (х, у, z), создаваемого непрерывным распределением масс по некоторому объему V, на основании (1.3) можно написать в виде (1.7), где ρdV=dm, ρ- плотность распределения массы элемента объема dV, dm-прирост массы.

Эта функция Φ (х, у, r) удовлетворяет уравнению Лапласа Φ (х, у, r) = 0 в точках, где нет масс.

Уравнение Лапласа для Φ равносильно уравнениям (1.8).

Можно показать при весьма общих практически приемлемых допущениях относительно распределения плотности ρ, что потенциал Φ гравитационного поля (1.7) для точек х, у, z, расположенных внутри V, удовлетворяет уравнению Пуассона (1.9).

Уравнение (1.9) равносильно уравнениям (1.10).

Практически приходится обычно иметь дело со слабыми гравитационными полями, для которых уравнения поля линейны. Для таких полей в первом приближении справедлив принцип суперпозиции. Волновое уравнение слабого гравитационного поля можно получить, если добавить вторую производную по времени в уравнение (1.9), превратив уравнение Пауссона в уравнение Д"Аламбера.

Математическая модель акустического поля

Акустика — область физики, исследующая упругие колебания и волны, их взаимодействие с веществом и применение.

Во всех средах (жидких, газообразных и твердых) распространение упругих волн происходит так: частицы среды в волне приобретают скорость, деформируются, и в них возникают упругие напряжения, которые и передают волну дальше.

Акустика жидкостей и газов рассматривается на основе гидродинамики, где возмущения передаются силами давления, которые возникают при сжатии и расширении частиц. В твердых телах возникают еще и поля (сдвиговые) упругих напряжений.

Математическая модель акустического поля представлена полной системой уравнений акустики, которая состоит из уравнений движении, уравнения непрерывности и уравнения состояния. Уравнения акустики кратко можно характеризовать так. [3].

Уравнения Эйлера — уравнения движения частиц под действием сил упругости среды. Рассмотрим ча­стицу среды малого объема, ограниченную поверхностью. Так как частица мала, а характеристики среды непрерывны, можем считать плотность по всей среде постоянной, массу частицы приравнять произведению плотности на объем. Далее, полагая, что вся частица движется как одно целое, найти ее ускорение как производную dv/dt ее скорости v по времени t. Рассмотрим давление p и сторонние cилы F а. ст, действующие на частицу со стороны окружающей среды, — силы давления.

Применяя к частице, находящейся под дей­ствием только сил давления, второй закон Ньютона и используя теорему Гаусса — Остроградского заменяя интеграл по поверх­ности интегралом по объему, а также учитывая непрерывности всех характеристик среды, что позволяет градиент давле­ния на протяжении малой частицы считать постоянным, получить уравнение Эйлера (2.1).

Если помимо сил давления на среду действуют сторонние силы Fа. ст, распределенные с плотностью ρ на единицу объема, то уравнение (2.1) примет вид (2.2).

Уравнение движения среды есть нелинейное векторное уравнение первого порядка относительно характеристик среды р, v, ρ.

Уравнение неразрывности среды. Если в среде не образуется разрывов (как, например, разрывы при кавитации), то уравнение неразрывности применимо к исследуемой среде.

Рассмотрим объем среды, ограниченный неподвижной по­верхностью S. Если разрывов нет, то приращение массы в объеме равно массе среды, втекшей через поверхность S. Запишем скорость прира­щения массы в малом объеме, массу, втекающая за единицу времени через элемент поверхности dS, равную v dS.

Заменяя интеграл по поверхности интегралом по объему, получим уравнение неразрывности в виде (2.3).

Уравнение неразрывности скалярно и, как уравнение Эйлера, нелинейно относительно характеристик среды. В дальнейшем встретятся случаи движения среды, удовлетво­ряющие вместо уравнения неразрывности уравнению вида (2.4).

Это уравнение можно также интерпретировать как уравнение не­разрывности, но примененное к среде, куда поступает «из ниоткуда» дополнительное «стороннее» количество среды. Величину Vст назы­вают плотностью сторонней объемной скорости: она дает допол­нительный объем, поступающий за единицу времени в единичный объем.

Уравнение состояния связывает давление, плотность (или сжатие) и температуру среды. Уравнение состояния не имеет какого-либо стандартного вида для всех веществ, наподобие урав­нения Эйлера или уравнения неразрывности. В общем виде уравнение можно записать в виде (2.5).

Уравнение состояния также нелинейно.

Если при данном движении среды плотность однозначно свя­зана с давлением (так бывает обычно в акустике), то уравнение состояния можно записать в виде (2.6).

Система уравнений (2.1), (2.3) и (2.5) или (2.6) является полной системой уравнений гидродинамики.

Волновое уравнение. Полная система уравнений гидродинамики это — нелинейные, точные уравнения. В дальнейшем будем пользоваться приближенными уравнениями линейного типа. Исключая все величины, характеризующую волну, кроме давления приведем полную систему уравнений акустики к одному уравнению относительно давления p (2.7).

Это волновое уравнение второго порядка для давления, где с — скорость звука.

Если записать выражение для давления гармонического колебания волн и затем подставить его в волновое уравнение (2.7), то получим волновое уравнения Гельмгольца (2.8).

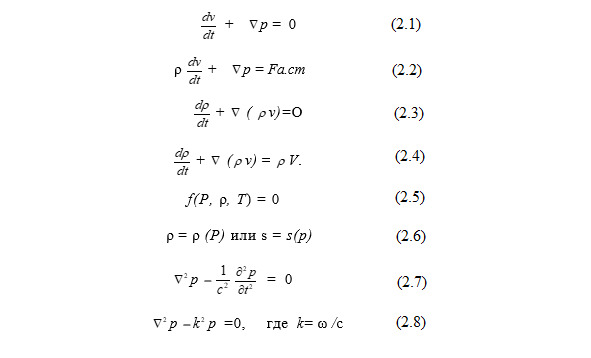
Математическая модель электромагнитного поля

Математическая модель электромагнитного поля представляет систему уравнений электромагнитного поля в полном виде или систему уравнений Максвелла [4].

Электромагнитное поле характеризуются следующими векторными величинами: E и H — векторы напряженности электрического и магнитного полей, D и B — векторы электрической и магнитной индукции, I и Im — плотность токов электрической и магнитной проводимости, ρ и ρm — плотность электрических и магнитных зарядов.

Дифференциальная форма системы уравнений выглядит (3.1 — 3.7), где — магнитная проницаемость, — диэлектрическая проницаемость, — удельная проводимость

Эти уравнения будут исходными при рассмотрение переменных электромагнитных полей и процессов.

Первое уравнение Максвелла. является дифференциальной формулировкой закона полного тока. Физический смысл 1-го уравнения Максвелла: источниками вихревых магнитных полей являются токи проводимости и токи смещения.

Величина δ в правой части (3.1) есть плотность тока проводимости. Это вектор, указы­вающий направление движения зарядов.

Законы электромагнетизма — это законы макро­скопических процессов, в которых усредняется действие огромных количеств элементарных частиц материи. С точки зрения этих законов, среда представляется сплошной.

Второе уравнение Максвелла (3.2) является дифференциальной формулировкой закона электромагнитной индукции и выражает скорость изменения магнитной индукции В через пространственную производную (rot) напряженности электрического поля Е.

Физический смысл: вихревое электрическое поле создается переменным магнитным полем

Третье уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для электрических полей. Физический смысл: источниками электрического поля (векторов Е и D) являются заряды с плотностью ρ. Дифференциальные уравнения (3.3) показывает, что расходимость электрической индукции равна объемной плотности заряда.

Четвертое уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для магнитных полей. Физический смысл. Дивергенция вектора В в любой точке пространства равняется нулю, т.е. — источников нет (магнитные заряды в природе отсутствуют). Нет ни стыков, ни источников. Линии магнитной индукции непрерывны.

Из уравнений (3.1) и (3.3) можно прийти к уравнению (3.8).

Это уравнение непрерывности. Закон сохранения заряда.

Уравнения (3.5), (3.6), (3.7) характеризуют связь векторов поля с материальной средой.

Установим волновой характер ЭМП. При распространении ЭМП с конечной скоростью происходит запаздывание его по фазе, результатом чего является волновой характер распространения. Можно записать первые два уравнения Максвелла в комплексной форме и заменить в них индукции B и D напряженностями rot E и rot H и ввести функцию комплексной диэлектрической проницаемости проводящей среды при монохроматическом поле. Затем получится полная система уравнений монохроматического ЭМП с комплексными проницаемостью и напряженностями E и H. Волновой характер ЭМП этого гармонического во времени процесса в области без источников получается, если исключить вектор E или вектор H из в уравнениях (3.1) и (3.2), применив оператор rot и учитывая, что расходимость (div) вектора H = 0.

Для однородной непроводящей среды волновое уравнение переходит в уравнение Гельмголца, которое запишется в уравнения (3.9 — 3.10), где k = ω εμ — волновое число.

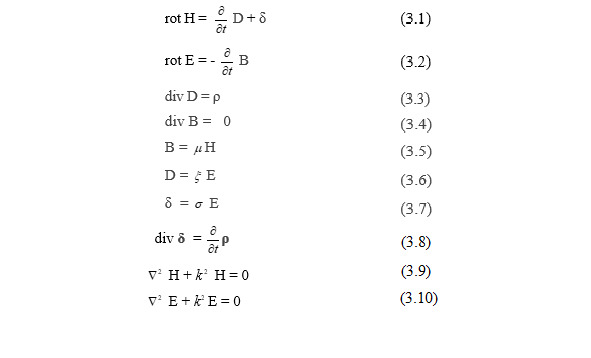
Об аналогии описания физических полей

Из рассмотренных математических моделей физических полей микромира видно, что гравитационное, акустическое и электромагнитное поля описываются при определенных условиях волновыми уравнениями (1.9, 2.7, 2.8, 3.9, 3.10). Мы имеем ситуацию, когда различные физические явления (поля) описываются аналогичными дифференциальными и другими уравнениями. То есть между физическими явлениями существует аналогия, которая основывается на сходстве уравнений, лежащих в основе описания данных физических явлений

Аналогия ЭМП и акустического поля.

Например, акустические волны описываются уравнениями Гельмгольца (2.8). Электромагнитные волны описываются уравнениями Максвелла, которые после соответствующих преобразований также переходят в уравнения Гельмгольца для однородной среды (3.9). Т.е. в двумерном случае уравнения Максвелла сводятся к двум независимым уравнениям для векторов напряженности электрического и магнитного полей (4.1 — 4.2).

Такие же уравнения можно записать для каждой из составляющих векторов вдоль осей x, у, z. В результате для каждой составляющей получаем уравнение Гельмгольца. Поэтому в двумерном случае решения акустических и электромагнитных задач совпадают. Однако при сопоставлении решений задач необходимо привести в соответствие и граничные условия. Рассмотрим примеры [5].

При абсолютно мягкой поверхность (для ЭМП-абсолютная проводящая поверхность и для АП–давление на поверхности равно нулю), если электромагнитная волна, падающая на поверхность имеет Е-поляризацию (вектор Е параллелен оси y),решениедля вектора Е полностью переносится на величину звукового давления р для абсолютно мягкой поверхности.

При абсолютно жесткой поверхности решение для вектора H, поляризованного параллельно образующей оси y, переносится на величину звукового давления p для абсолютно жесткой поверхности.

Промежуточный случай для электромагнитных волн, когда векторы E и H не параллельны границам раздела, распадается на два рассмотренных случая.

Задача об отражение звуковых волн от плоской границы раздела двух различных сред аналогична задаче об отражения ЭМВ от плоской границы двух диэлектрических сред. Было получено, что аналогом звукового давления р в рассматриваемой задаче будет Еу, а аналогом нормальной составляющей колебательной скорости Vz — величина Нх. Выражение, определяющее коэффициент отражения для вектора E=Еу, будет аналогично формуле для коэффициента отражения звуковой волны (по давлению).

Для акустических волн сохраняется известный закон преломления в оптическом диапазоне ЭМВ. Сохраняются также другие закономерности.

В трехмерном случае за редким исключением векторные уравнения Максвелла не сводятся к скалярным, и найти решения для электромагнитных волн, которые бы соответствовали и звуковым волнам, невозможно. Однако несоответствие между решениями акустических и электромагнитных задач постепенно уменьшается при увеличении волнового размера тела.

Поэтому все результаты, полученные в теории излучения электромагнитных волн, остаются справедливыми и в акустическом случае.

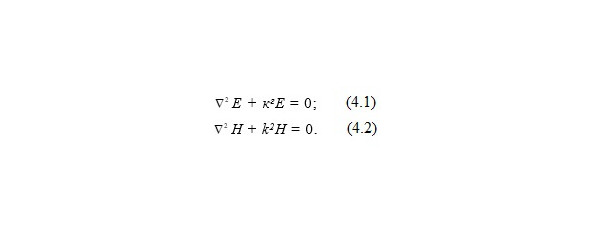
Аналогия ЭМП и гравитационного поля

В математической модели гравитационное поле описывается уравнениями (1.9 и 1.10). Покажем, что это уравнение аналогично уравнению Максвелла для электростатического поля. Так как задача определения потенциала гравитационного поля и силы, действующей со стороны поля на пробную единичную массу, может быть поставлена как задача об определении функции Φ (х,у,z), исчезающей в бесконечности и удовлетворяющей уравнению Лапласа всюду вне V и уравнению Пуассона всюду внутри V, или как задача определения сил F, удовлетворяющих уравнениям (1.8) и (1.10). Такого рода постановка задачи в теории ньютоновского потенциала полностью аналогична постановке задачи электростатики на основе уравнений Максвелла. Можно показать, что решение в бесконечном пространстве задачи об отыскании функции Φ (х,у,z) исчезающей в бесконечности, приводит к формуле (1.7), выражающей собой закон гравитационного тяготения.

Векторной характеристикой гравитационного поля является его напряженность — силовая характеристика точки поля тяготения, равная отношению силы тяготения F, действующей на помещенную в него материальную точку к массе этой точки m.

Предположение о существовании гравитационных волн есть один из вариантов решения уравнений Эйнштейна.

Существование электромагнитных волн также было результатом одного из возможных решений уравнений Максвелла (переменное движение электрических зарядов и переменные электрические токи являются источниками электромагнитных волн).

Точно также считается, что переменное движение массы приводит к излучению гравитационных волн. В настоящее время гравитационные волны определяют как переменное гравитационное поле, распространяющееся со скоростью света и проявляющееся в возникновении относительных ускорений тел.

Интерпритация модели для реальных объектов защиты информации

На рис.2 представлена реальная картина наличия физических полей, их суперпозиция и взаимодействия для простого объекта информатизации, в качестве которого выбрано автоматизированное рабочее место на базе одного персонального компьютера. Разнообразие параметров физических полей представлено напряженностью электрического поля E, напряженностью магнитного H и электромагнитного E,H полей, частотой f, коэффициентом модуляции, спектром сигнала, напряжением, током и другими параметрами.

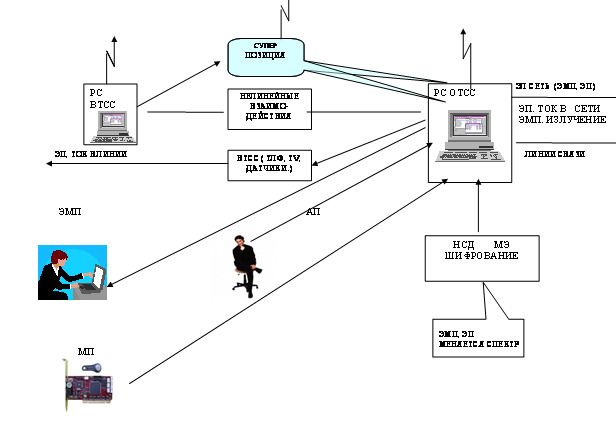
Рис.3 отражает картину акустического поля, его суперпозицию и нелинейные взаимодействия на примере помещения, где циркулирует защищаемые акустические поля. Поле характеризуется такими параметрами: как: частота f, давление P, колебательная скоростьVk, ускорение а, разборчивость речи W и др.

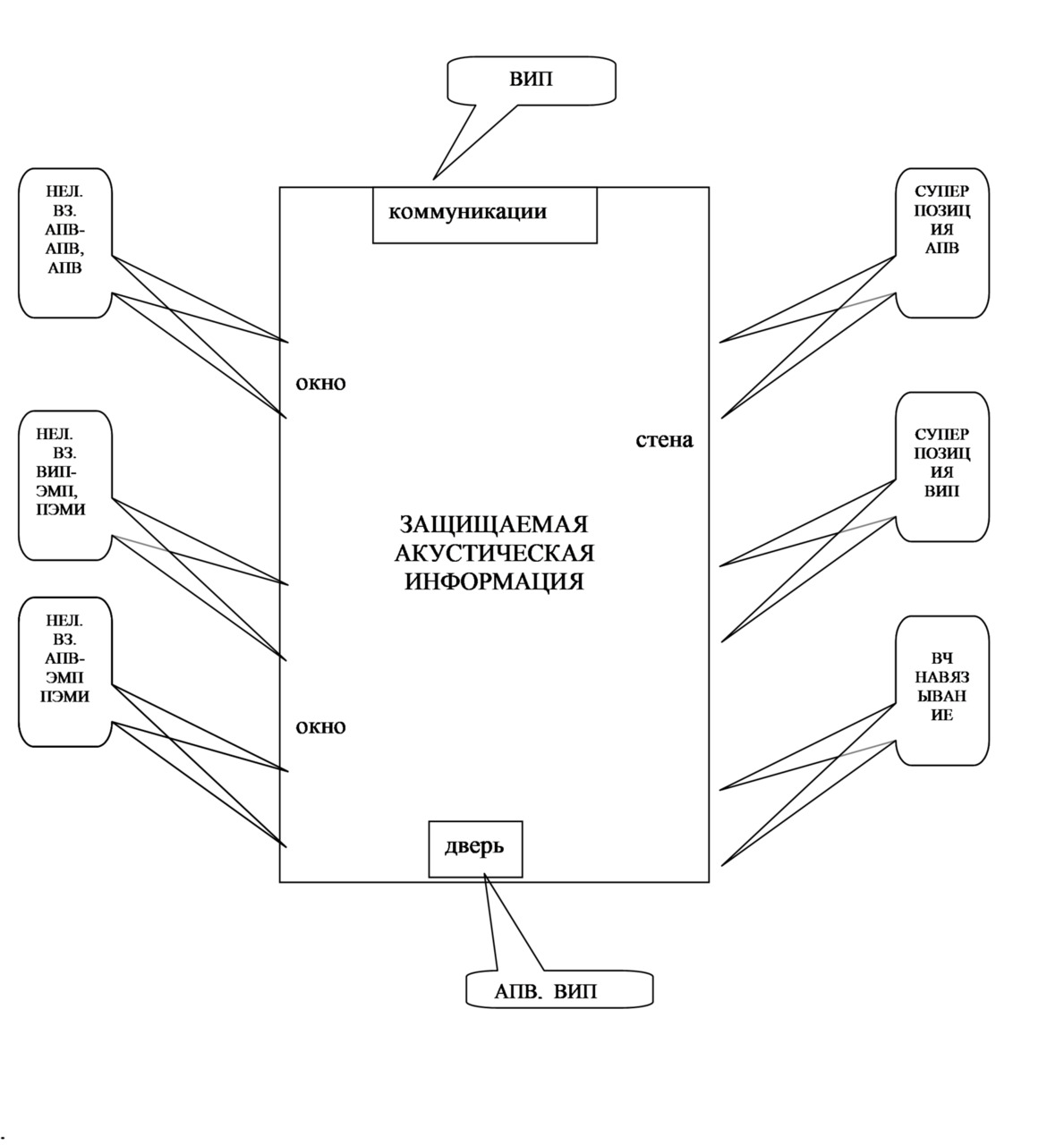
Вывод

1 Введено понятие информации как физическое поле.

2 Показано, что вся информация, сформированная и воспринимаемая — это физическое поле или суперпозиция и взаимодействие полей.

3 Представлена математическая модель физических полей.

4 Показана аналогия описания и изучения физических полей с помощью волновых уравнений.

5 Материал данной работы является исходными данными для реализации модели исследования согласно Рис. 1.

Взаимодействие полей

Исследование взаимодействия физических полей для задач защиты информации

Рассмотрим информацию как многообразия физических полей, их суперпозиции и нелинейных взаимодействий. Взаимодействие составляющих физических полей показаны на рисунке 4.

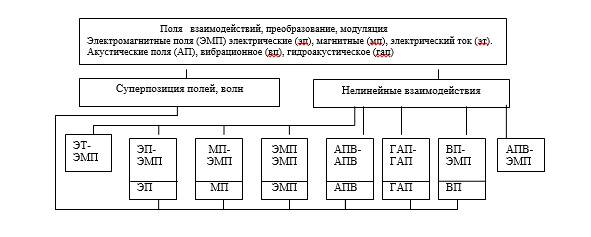
Модель линейных взаимодействий

Отклик или реакция среды на внешнее воздействие физического поля или результат взаимодействия физических полей обозначим буквой О. Воздействия — В.

В отсутствие нелинейных структур, сред, элементов результат взаимодействия описывается линейной зависимостью (5.1),где α — восприимчивость воздействия.

Линейность описывает выполнение принципа суперпозиции (наложения, сложения). Линейные процессы, линейные закономерности и линейные зависимости встречаются часто в физических системах и в процессе взаимодействия.

Линейность предполагает выполнение принципа суперпозиции (наложения, сложения). В этом смысле линейность — категория конструктивная. Зная результат действия каждой из двух (или многих) сил на тело заданной массы и пользуясь принципом суперпозиции, можно ответить на вопрос: «Как будет двигаться это же тело под действием суммарной силы?». Это же можно сказать и о действии суммарного электрического или магнитного полей. Примеры можно продолжить

В природе встречаются линейные процессы, линейные закономерности и линейные зависимости. Как теперь стало понятно, линейные закономерности скорее исключение.

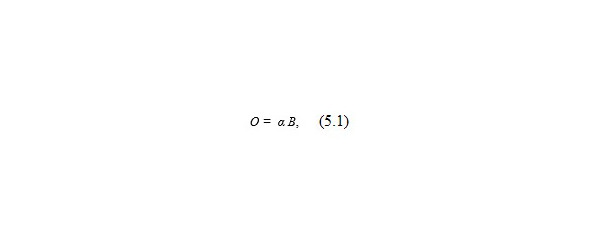
Рассмотрим суперпозицию ЭМП-ЭМП и поляризацию

ЭМП рассматривали как волновой процесс, который описывается однородным уравнением Гельмгольца (6.1), где (6.2) — оператор Лапласа, (6.3) — волновое число или постоянная распространения, (6.4) — абсолютные диэлектрическая и магнитная проницаемости, (6.5) — относительные диэлектрическая и магнитная проницаемости.

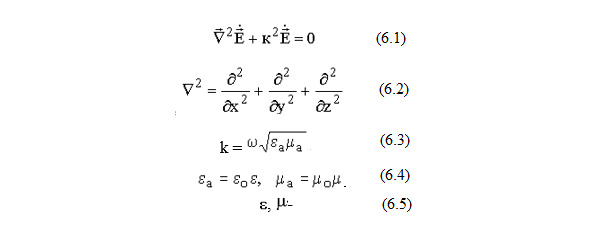
Рассмотрим плоскую электромагнитную волну. Это волновой процесс, у которого амплитуды электрической и магнитной составляющих поля во всех точках плоскости, перпендикулярной направлению распространения волны, имеют одинаковые значения.

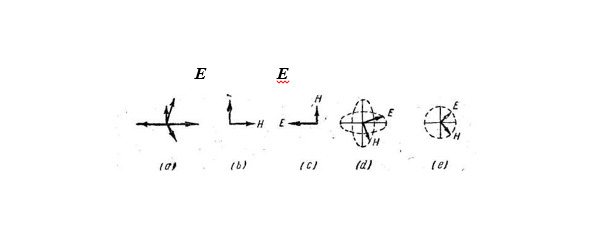
Волновое уравнение для плоского поля является линейным дифференциальным уравнением, сумма нескольких его решений также будет являться решением этого уравнения. Таким образом, сложные типы электромагнитных волн можно представлять себе составленными из большого числа элементарных плоских волн с различными амплитудами, фазами и направлениями распро­странения. В большинстве практических задач, однако, эта точка зрения имеет лишь методиче­ское значение; методы количественного анализа для таких задач будут рассмотрены ниже. Лишь в случае, когда элемен­тарные плоские волны распространяются в одном и том же направлении, имеет смысл вместо суммарной волны рассматривать её элементарные составляющие и находить суммарные свойства путём суперпозиции свойств составляющих. Для таких сложных волн ориентация векторов поля описывается понятием поляризации волны (рис.5).

Для элементарной плоской однородной волны векторы электрического и магнитного полей всегда взаимно перпенди­кулярны в любой точке пространства.

Сочетание элементарных волн, распространяющихся в одном направлении, при произволь­ной ориентации их векторов поля, называется неполяризованной волной. Её отдельные составляющие волны могут иметь также произвольные амплитуды и фазы [рис.].

Если векторы поля для всех элементарных волн, распространяющихся в одном направлении, сохраняют одно и то же общее направление, то суммарная волна называется плоскополяризованной. Здесь может возникнуть вопрос, относятся ли эти определения только к волнам одной и той же длины или нет. В радиотехнике чаще всего приходится иметь дело с волнами, распространя­ющимися в свободном пространстве, для которого постоянная распространения не зависит от частоты; поэтому вышеприведенные определения относятся к волнам любой длины. Тем не менее, в случае волны, составленной из двух элементарных волн различной длины и имеющих общее направление распро­странения и ориентацию векторов поля, мы предпочтительнее будем говорить не о суммарной волне, а о двух элементарных волнах с одинаковой поляризацией, но имеющих различную длину.

Плоскость поляризации обычно определяется в радиотех­нике ориентацией вектора электрического поля, в противопо­ложность оптике, где принято, что плоскость поляризации» совпадает с вектором магнитного поля. Таким образом, согласно радиотехнической терминологии, волны с вектором электриче­ского поля, направленным вертикально, будут называться вертикально поляризованными. Волны с горизонтально на­правленным электрическим вектором будут называться горизон­тально поляризованными [рис. (b) и (с)].

Сочетание двух однородных плоских волн, отличающихся по амплитуде, фазе и ориентации векторов поля, но имеющих одну и ту же длину, называется эллиптически поляризованной волной. Для того чтобы уяснить смысл этого термина, мы разложим каждую из элементарных волн на две одну с элек­трическим вектором, направленным вдоль оси х, и другую — вдоль оси у. Сложим теперь обе волны, имеющие электрический вектор в направлении x; в результате мы получим волну определённой амплитуды и фазы, которая запишется, если воспользоваться тригонометрическим выражением, в виде (6.6).

Две волны, имеющие электрический вектор в направлении у, дадут, в результате их сложения другую волну, отличную от первой по амплитуде и фазе (6.7).

Для некоторой плоскости, например z = 0, оба выражения упрощаются (6.8 — 6.9).

Это является уравнением эллипса в параметрической форме: конец вектора электрического поля вычерчивает в плоскости, перпендикулярной к направлению распространения, эллипс. Это обстоятельство и служит поводом для названия «эллипти­ческая поляризация» [рис. (d)].

Если исходные волны таковы, что составляющие по осям xи уравны по амплитуде и расходятся по фазе на 90°, эллипс вырождается в окружность, и волна обладает

круговой поляризацией. Действительно, если (6.10 — 6.11), что является уравнением окружности, рис.

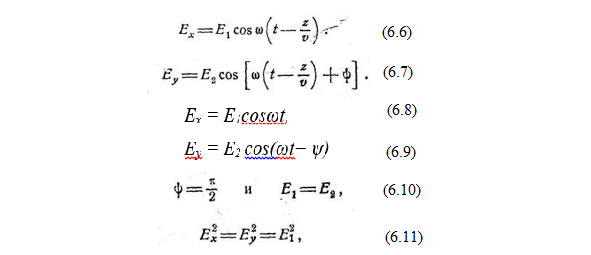
Линейные закономерности можно рассматривать как частный случай нелинейных.

Суперпозиция акустических волн

В практике защиты информации мы будем иметь акустические и звуковые волны, которые распространяются в газообразных, жидких и твердых средах. Для жидкости и газа могут существовать только продольные волны, для которых направление колебаний частиц среды совпадают с направлением распространения волны. Эти волны мы будем сейчас рассматривать. Точнее рассмотрим плоскую волну, у которой фронт представляет собой плоскость

Если через некоторую точку среды проходит ряд гармонических волн, то колебания при малых амплитудах суммируются (принцип суперпозиции), т. е. результирующее колебание равно сумме ко­лебаний, создаваемых отдельными волнами. Возникает явление интерференции волн. При ин­терференции гармонических волн амплитуда результи­рующего колебания определяется по следующему прави­лу: если складываются гармонические колебания одина­ковой частоты, то вектор результирующего колебания является суммой векторов составляющих колебаний (рис. 5). Амплитуда и фаза результирующего колеба­ния зависят, следовательно, от отношения между фаза­ми слагаемых колебаний.

Рассмотрим основные соотношения, касающиеся интерференции волн. Пусть в некоторую точку С среды доходят гармонические колебания, распространяющиеся от двух источников 1 и 2 (рис. 6). Если считать, что фазы колебания источников одинаковы (синфазные источники), то сдвиг фаз φ колебаний, достигших точки С, зависит лишь от разности ε расстояний от источников до рассматриваемой точки или, иначе говоря, от раз­ности хода лучей. Разность фаз φ определяется форму­лой (7.1) т. е. отношением разности хода лучей к длине волны.

Если амплитуды слагаемых колебаний одинаковы и равны а, то, складывая векторы, соответствующие этим колебаниям (рис. 7), найдем величину А вектора результирующего колебания (7.2), где Ат=2а — максимальная амплитуда. Подставляя φ = 2лε/λ,, получим (7.3).

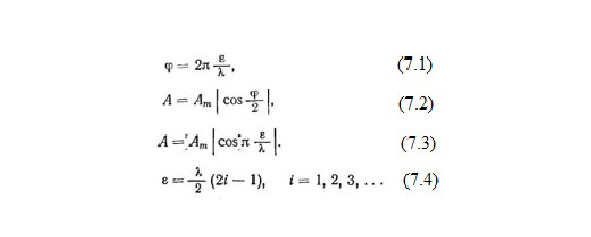
Рассматривая амплитуду результирующего колеба­ния, мы всегда будем иметь в виду абсолютное значе­ние величины А. Как видим, амплитуда результирующе­го колебания зависит от отношения разности хода к длине волны λ. Если разность хода лучей равна цело­му числу длин волн, то колебания складываются в фазе и амплитуда результирующего колебания равна удвоенной амплитуде слагаемых колебаний Если разность хода лучей равна нечетному числу полуволн, то колеба­ния складываются в противоположных фазах и в ре­зультате получится ноль.

Таким образом, максимум Ат=2а будет при условии ε=λ i, i=l, 2, 3, …, минимум A= 0 при (7.4).

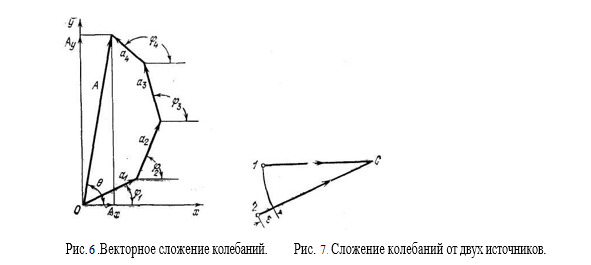
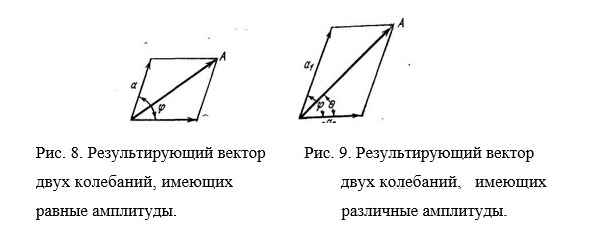
Накладываются две волны с неравными амплитудами а1 и а2 (рис.9)

Определяя амплитуду А результиру­ющего колебания, получим (7.5). Максимальная амплитуда равна а1 + а2 при ε=λ i. Минимальная амплитуда равна а1 — а2 при ε= λ/2 (2i-1).

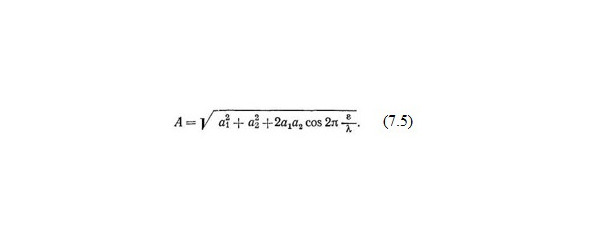
Амплитуда результирующего колебания А в случае сложения п волн

Обратимся к векторной диаграмме изображенной на рис. 1. Проведя оси х и у, имеем (8.1), где Ах и Ау — проекции замыкающей на оси х и у. Так как проекция замыкающей равна алгебраической сум­ме проекций ах и av составляющих многоугольника, то из этого следует (8.2). Поэтому уравнение примет вид (8.3).

Подставляя ах и av получим (8.4), где α амплитуды слагаемых колебаний; φ- фазы слагаемых колебаний.

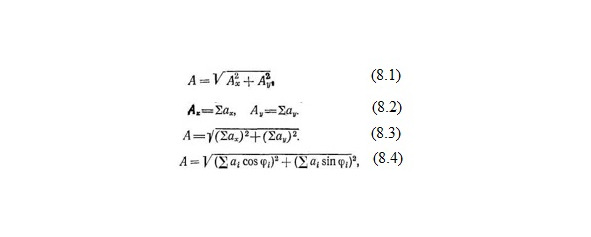
Для фазы θ результирующего колебания амплитуда равна А θ = А cos θ.

Модель нелинейных взаимодействий

При наличии нелинейности или проявлении ее при интенсивных воздействиях восприимчивость α становится нелинейной функцией внешнего воздействия и тогда отклик системы: О = αн В

Рассмотрим нелинейное преобразование различных воздействий физических полей. Результат воздействия на нелинейную среду Вi (t) соответствующих i воздействий (i = 1,2,3…n).

Пусть среда, область взаимодействия полей характеризуется амплитудной функцией преобразования выходного параметра, отклика О от входного воздействия В полиномом k–той степени, которая записывается (9.1).

На область взаимодействия поступает воздействие различных градаций параметров поля, которое характеризует воздействия суммы n излучений и определяется функцией (9.2). Результат нелинейного преобразования процесса В (t) запишется (9.3), где bk — определяет крутизну нелинейной функции взаимодействия. Представленную модель взаимодействия применяют для описания любых физических полей.

Для примера, рассмотрим взаимодействия полей (электромагнитных или гидроакустических) с амплитудной функцией нелинейности, которая характеризуется полиномом третей степени (k=3). Тогда характеристика поля (напряженность поля или уровень давления) при синусоидальном входном воздействии запишется так:

Ввх = В1 +В2 =В1соsω1+ В2 cosω2. В результате взаимодействия по расчету будем иметь основные частоты ω1, ω2, 2ω1, 3ω1, частоты от квадратичного члена полинома ω1 ± ω2, частоты от кубического члена 2ω1- ω2; 2ω2- ω1.

В общем случае возникают комбинационные колебания на частотах nfi ± k fi от квадратичных, кубичных и k-ых степеней полинома, описывающего воздействия. Натурные измерения, которые выполнялись автором в различные периоды на нелинейных средах и элементах для ЭМП, ЭП, ГАП, показали наличие комбинационных частот. Один из результатов приведен в /2/.

При воздействии на физическую систему различных полей важно учитывать состояния, поведения системы. В линейных системах имеется одно состояния равновесия. Если система нелинейная, то могут существовать несколько состояний равновесия. Устойчивое состояние сохраняется, неустойчивое не сохраняется. Имеются разные критерии состояния (Гурвица, Ляпунова и др.), когда физическая система описывается системой n-дифференциальных уравнений.

Часто применяют уравнение вида (9.4), где функция f (v, dv/dx) в общем случае является нелинейной, а е (х) представляет собой периодическую внешнюю силу; τ — безразмерное время; τo — период внешней силы, воздействия.

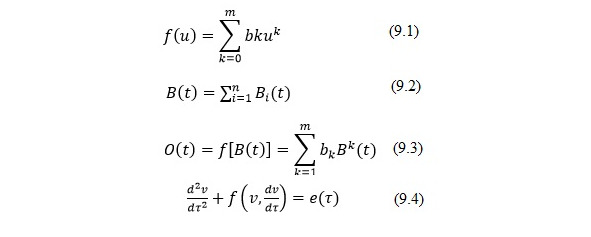
Важно, что в одной и той же нелинейной системы могут существовать различные виды периодических колебаний.

Рассмотрим характерные виды колебаний.

1. Случай гармонических колебаний, в которых основная составляющая преобладает над более высокими гармоническими колебаниями.

2. Если условия устойчивости нарушаются, то происходит аномальное возбуждение ультрагармоник на частотах f 1гор, f 2гор… f iгор.

3. Субгармонические колебания с основной частотой f iсуб.= f осн. (1/ n), где (n=2,3,4) возникают на нелинейностях и относятся к определенному типу нелинейных колебаний.

Приведенную модель можно использовать для основного класса взаимодействий физических полей.

Нелинейный эффект — это эффект, описываемый нелинейной зависимостью, нелинейным уравнением. Нелинейная теория — это теория, в основе которой лежат нелинейные связи между объектами. Совсем простое нелинейное уравнение может иметь бесчисленное множество решений. Множеству решений соответствует множество путей эволюции нелинейной системы и тогда эта система может пойти по одному или качественно иному пути развития.

Разные процессы в разных естественных науках (физики, химии, биологии и др.), а также в экономике, социологии, медицине, в технических приложениях описываются одинаковыми или сходными моделями. Эти модели предсказывают сходные конечные результаты.

В решении проблемы комплексной защиты объектов информатизации задачи защиты информации прежде всего следует рассматривать как изменение физических полей. Многообразие физических полей и особенно продуктов взаимодействия, например, таких как наличие большого класса излучений ставит задачу скрытия и изменения характеристик поля в задачах защиты информации. Требуется энергетические затраты и использование технических средств. Наличие широкого спектра частот с другой стороны говорит о «размазывании» сигнала в пространстве физического поля, что является показателем скрытности, большой базы сигнала. И тогда имеется путь повышения эффективности защиты в создании технических средств обработки информации с большой базой.

Электромагнитное поле

Вид электромагнитного излучения

Электромагнитное излучение характеризуется частотным диапазоном от постоянного тока до рентгеновского (3.1019 Гц) и радиационного излучения. Ниже приводится шкала частот и длин волн электромагнитного излучения. По горизонтальной оси отложены: внизу λ — длина волны в метрах; вверху ν — частота колебаний в герцах. Чаще частота обозначается буквой f или F.

Длины электромагнитных волн радиодиапазона заключены в пределах от 10 км до 0,001 м (1 мм). Диапазон от 1 мм до видимого излучения (т. е. 760 нм) называется инфракрасным диапазоном. Электромагнитные волны с длиной волны короче 390 нм называются ультрафиолетовыми волнами. Наконец, в самой коротковолновой части спектра лежит излучение рентгеновского и гамма-диапазонов.

Всякое излучение можно рассматривать как поток квантов — фотонов, распространяющихся со скоростью света, равной c = 3.108 м/с. Скорость света связана с длиной и частотой волны соотношением (10.1).

Энергию квантов света E можно найти, зная его частоту: E = hν, где h — постоянная Планка, равная h ≈ 6,626∙10–34 Дж∙с. Энергия квантов измеряется в джоулях или электрон-вольтах: 1 эВ = 1,6∙10–19 Дж. Кванту с энергией в 1 эВ соответствует длина волны λ = 1240 нм.

Глаз человека воспринимает излучение, длина волны которого находится в промежутке от λ = 390 нм (фиолетовый свет) до λ = 760 нм (красный свет). Это — видимый диапазон.

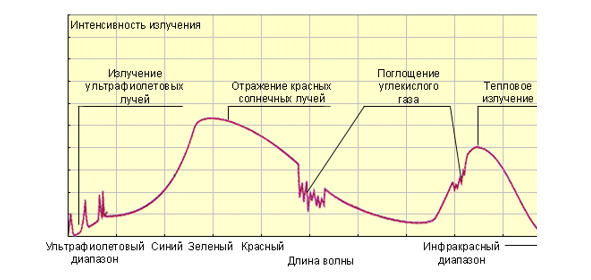
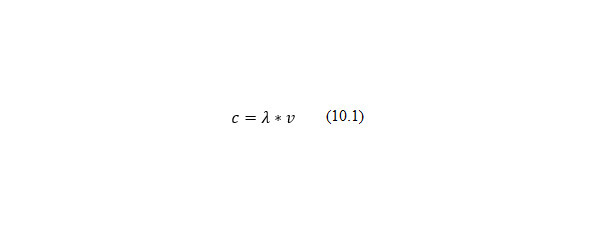
Излучение в видимой области спектра играет основную роль в жизни человека и хорошо пропускается земной атмосферой. Во многих других участках спектра земная атмосфера поглощает излучение. Видимая область спектра регистрируется оптическими телескопами, а также невооруженным глазом. Глаз — это естественный измерительный прибор, регистрирующий электромагнитное излучение в видимой области спектра.

Площадь зрачка может изменяться в 100 раз, тем самым регулируя поток света, поступающего на сетчатку в дневное время. Днем освещенность от Солнца составляет 105 лк; в то время как ночью звездное небо создает освещенность всего в 10–5 лк. Поэтому для того, чтобы видеть в темноте, регистрировать излучение должны не колбочки, а палочки — другие элементы глаза. Максимальная чувствительность глаза при дневном зрении приходится на длину волны λ = 555 нм и соответствует желто-зеленому цвету. Ночью она сдвигается в коротковолновую часть спектра λ = 513 нм. Лабораторные исследования показали, что ночью глаз может зарегистрировать изменение звездной величины на 0,1m.

Ниже представлены виды ЭМП, АП, спектр, энергия и мощность

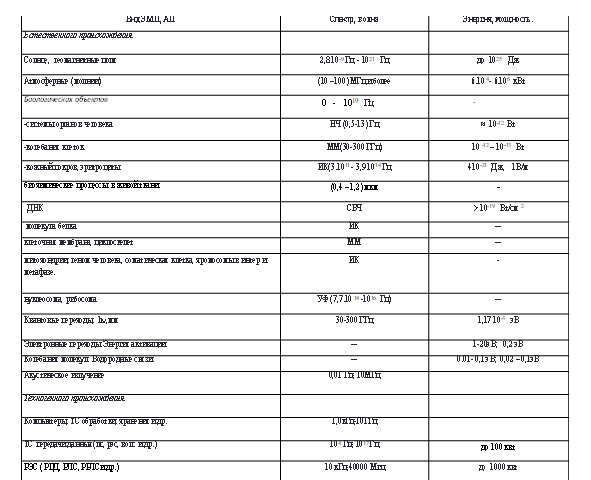
Энергия ЭМИ

Рассмотрим ЭМИ следующих спектральных диапазонов:

электромагнитное ионизирующее излучение с длиной волны от 5.10~4 до 0,01 нм (у-излучение) и от 0,01 до 6 нм (рентгеновское излучение);

Ультрафиолетовое (УФ) излучение от 0,05 до 0,4 мкм;

Видимое излучение от 0,4 до 0,77 мкм; инфракрасное (ИК) излучение от 0,77 до 1000 мкм; сверхвысокочастотное (СВЧ) излучение от 1 мм до 3м.

Специфика воздействия ЭМИ в основном объясняется различ­ными значениями энергий квантов соответствующих частот. Энер­гия кванта WKB связана с частотой излучения ν следующей зависимостью: Wm = νf,

где h — постоянная Планка, равная 6,62—10~34 Дж-с. Если энер­гию кванта измерять в электрон-вольтах, а длину волны излуче­ния λ в нанометрах, то имеем преобразование:

WKB=1240/λ, 1 ГэВ = 109 эВ, 1 эВ = 1,6*10—12 эрг = 1,6*1019 Дж.

Минимальная энергия кванта, способная вызвать ионизацию воды и атомов кислорода, водорода, азота и углерода, составля­ет 12 … 15 эВ [66]. Энергию кванта 12 эВ можно рассматривать как нижний предел ионизации для биологических систем. Этой энергии соответствует Х,= 100 нм. Квант электромагнитного излу­чения, в зависимости от энергии, может вызвать ядерные превра­щения, ионизацию атомов вещества или возбуждение электрон­ных оболочек. В биологических системах поглощение квантов ЭМИ неионизирующих уровней энергии может приводить к дис­социации молекул при передаче энергии электронам связи, рас­сеянию энергии возбуждения в виде флуоресцентного или фосфоресцентного излучения, к образованию свободных радикалов, к превращению энергии излучения в энергию колебательного, вра­щательного, поступательного движения молекул, т. е. в теп­ло.

Биологический эффект воздействия ЭМИ на живые организмы зависит как от энергии квантов ЭМИ, так и от глубины проник­новения излучения в систему, способности участвующих в процес­се взаимодействия молекул испытывать в результате поглощения энергии химические превращения, а также от других физико-би­ологических факторов. Важное значение имеют энергия и мощность излучения.

Характерная энергия объединения оценивается по порядку величины как 102 ГэВ (ГэВ — это сокращенное от гигаэлектрон-вольт, 1 ГэВ = 109 эВ,

1 эВ = 1,6*10—12 эрг = 1,6*1019 Дж). Для сравнения отметим, что характерная энергия электрона в основном состоянии атома водорода порядка 10—8 ГэВ, характерная энергия связи атомного ядра порядка 10—2 ГэВ, характерная энергия связи твердого тела порядка 10—10 ГэВ. Таким образом, характерная энергия объединения электромагнитных и слабых взаимодействий огромна по сравнению с характерными энергиями в атомной и ядерной физике. По этой причине электромагнитное и слабое взаимодействия не проявляют в обычных физических явлениях своей единой сущности.

Общая картина разделения единого великого взаимодействия на отдельные сильное, слабое и электромагнитное взаимодействия выглядит следующим образом. При энергиях порядка 1015 ГэВ и выше существует единое взаимодействие. Когда энергия становится ниже 1015 ГэВ, сильное и электрослабое взаимодействия отделяются друг от друга и представляются как различные фундаментальные взаимодействия. При дальнейшем уменьшении энергии ниже 102 ГэВ происходит отделение слабого и электромагнитного взаимодействий. В результате на масштабе энергий, характерных для физики макроскопических явлений, три рассматриваемых взаимодействия выглядят как не имеющие единой природы.

Заметим теперь, что энергия 1015 ГэВ отстоит не так далеко от планковской энергии (11.1), при которой становятся существенными квантовогравитационные эффекты.

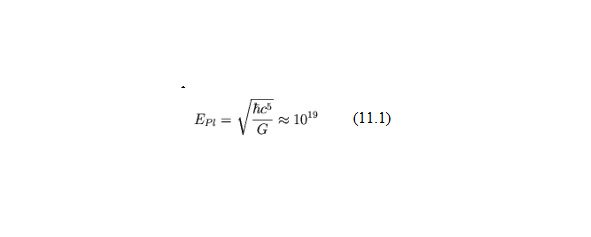
Излучения ЭМП

1. Элементарная антенна

Простейшим примером вычислении излучаемой мощности и расчёта поля вокруг антенны по известному распределению тока на поверхности антенны является вычисление в случае линейного элемента, выбранного настолько коротким, чтобы ток можно было считать неизменным по всей его длине. Позднее некоторые более сложные антенны мы будем рассматривать как бы состоящими из большого числа таких элементарных антенн, с соответствующими величинами и фазами токов в них. Мы будем рассматривать только случаи, когда ток изменяется синусоидально во времени. Соответственно, он может быть, выражен как J0 ejωt или, ещё лучше, через его амплитудное значение J0 с только подразумевающимся множи­телем ejωt.

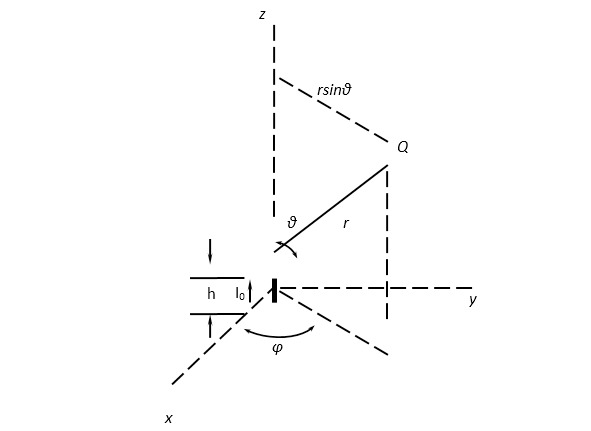
В качестве направления тока выбираем направление оси z. Элемент поместим в начале сферической системы координат (см. рис. 1).

Длину элемента h будем считать очень малой по сравнению с длиной волны.

Согласно третьему уравнению Максвелла, которое является дифференциальной формулировкой теоремы Гаусса для электрических полей. Физический смысл уравнения состоит в том, что источниками электрического поля (векторов Е и D) являются заряды с плотностью ρ. Дифференциальные уравнения показывает, что расходимость электрической индукции равна объемной плотности заряда (12.1).

Для случая переменных токов, когда установилось стационарное состояние системы и все величины изменяются пропорционально ejωt то есть, значение тока задано, определение полей может быть про­изведено с помощью запаздывающих потенциалов, рассмотренных в Л1. Было найдено подходящее для этих целей выражение для вектор-потенциала A. Так как вектор тока направлен по оси z, то и вектор-потенциал может быть только в этом направлении. Для любой точки Q, ра­диус-вектор которой равен r, век­тор А, согласно Л1, выразится простой формулой (12.2), или, в сферической системе координат (12.3 — 12.4) (рис.11).

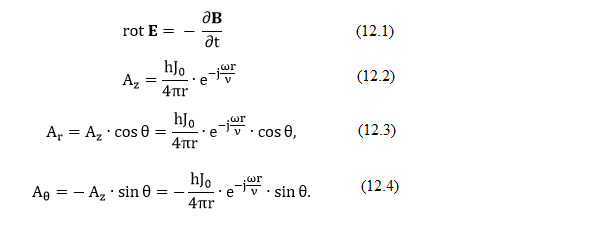
Вектор A не имеет соста­вляющей по углу φ и, кроме того, у него нет вариаций по φ вследствие симметрии системы относительно оси. Компонен­ты электрического и магнитного полей можно найти с по­мощью вектора А, пользуясь соотношениями, приведёнными в Л1 получаем (12.5 — 12.7), где k=ω/ν = ω√με = 2π/λ.

Для того чтобы вычислить средний поток энергии через окружающую элемент поверхность, можно взять поверхность любой формы и размеров. В частности, если поверхность находится на большом удалении, одни члены в приведённых выше формулах для компонент ноля становятся пренебрежимо малыми по сравнению с другими. Их можно было бы опустить сразу же, но они были оставлены с намерением выяснить некоторые свойства различных компонент. В области, очень близкой к элементу (r– мало), и в выражении для Нφ наибольшее значение имеет член, пропорциональный 1/r2. В выражениях для Еrи Еθ наибольшее значение имеют члены, содержащие 1/r3. Та­ким образом, в близкой к элементу области магнитное поле находится почти и фазе с током, и Hφ можно рассматривать как обычное поле индукции, определяющееся согласно закону Ампера. Электрическое поле в этой области можно рассматри­вать как поле электростатического диполя. (Если ток течёт только и одном направлении, положительный заряд должен собираться на одном конце, а отрицательный — на другом, что и объясняет появление решения для диполя.) Главные компо­ненты электрического и магнитного полей в этой области сдви­нуты во времени на 90°, так что, в соответствии с теоремой Пойнтинга, они не дают среднего во времени значения потока энергии.

На очень больших расстояниях от источника в вы­ражениях Е и Н наибольшее значение играют члены, содер­жащие только 1/r (12.8 — 12.10).

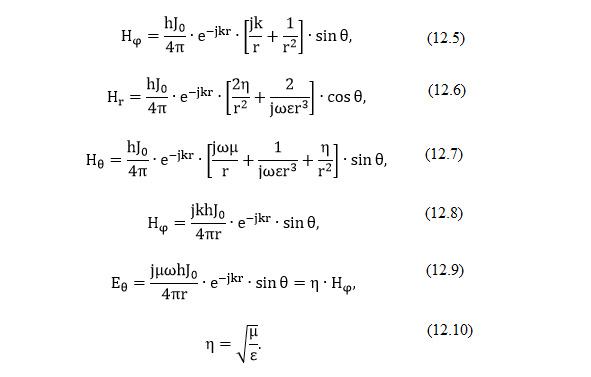
На больших расстояниях от источника любая часть сфери­ческой волны становится, по существу, плоской волной, так что появление приведённых выше выражений, типичных для однородных плоских воли, не является неожиданным Еθ и Hφ изменяются синфазно. Отношение Еθ к Нφ равно η. Векторы Е и Н направлены под прямым углом друг к другу и к на­правлению распространения. Вектор Пойнтинга при такой ори­ентации векторов Е и Н будет направлен по радиусу.

Зоны излучения ЭМП

Другой подход к определению закона изменения уровня электромагнитного поля можно рассматривать как в книги Гольдштейн, Л. Д. Зернов, Н. В. Электромагнитные поля и волны. М.: Советское радио, 1956 г.

После решения волновых уравнений получены следующие выражения для расчета уровня электромагнитного поля.

В общем виде поле, создаваемое элементарным электрическим (или магнитным) вибратором в какой-либо точке, состоит из не­скольких составляющих, величины которых зависят от направле­ния излучения, излучаемой длины волны и расстояния г от излучающего вибратора. В сферической системе координат дей­ствующие значения составляющих поля (без учета фазы) имеют вид (13.1 — 13.4).

Для электрического вибратора (13.5 — 13.6).

Для магнитного вибратора (рамки) (13.7 — 13.8).

Где θ — угол между осью диполя или осью рамки (витка), перпен­дикулярной к ее плоскости, и направлением на точку, где определяется поле;

Eθ и Еφ — тангенциальные составляющие вектора напряженности электрического поля в плоскости, параллельной оси вибратора, и в, плоскости, перпендикулярной оси вибратора;

Hθ и Hφ — соответствующие составляющие вектора напряженности магнитного поля;

Еr и Нr — соответственно радиальные составляю­щие векторов электрического и магнитного полей;

Iа — ток антенны, равномерно распределенный по всей длине вибратора;

μ, ε — соот­ветственно магнитная и диэлектрическая проницаемости воздуха.

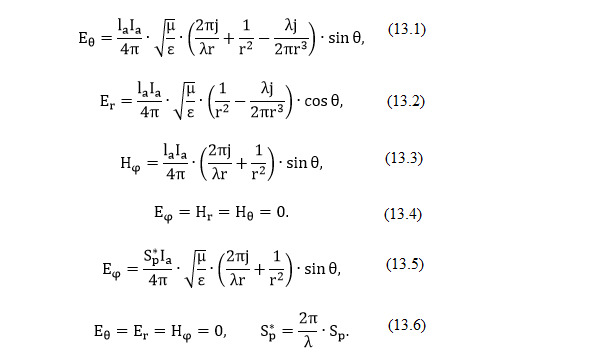
Все составляющие полей вибраторов (пропорциональные 1/г, 1/г2, 1/г3) требуется учитывать, когда приемная антенна находится в промежуточной зоне, ограниченной пределами r = λ/2π и r = 10λ.

В ближней зоне, т. е. на расстоянии r <<λ, преобладают со­ставляющие, пропорциональные 1/r3 для Eθ, Er, Нθ и Нr и пропор­циональные 1 /r2 для Eφ, Нφ.

Вариант интерпретации напряженности поля в ближней и промежуточной зоне.

Из представленного выше выражения для Eθ (13.7).

Наибольший интерес представляет поле в ближней и промежуточной зоне. Закон изменения уровней напряженности электромагнитного поля, измеренного на единичном расстоянии E0, в зависимости от расстояния, имеет вид (13.8).

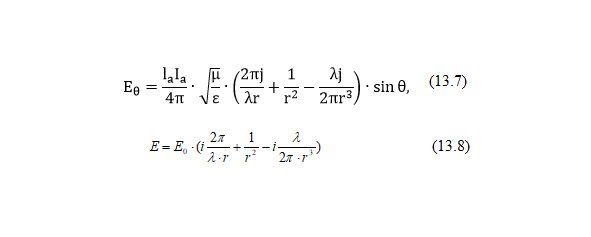
Построим и проанализируем график изменения каждой составляющей поля, а также суммарную напряженность. Он представлен на рисунке.

Пунктирными линиями показаны все составляющие поля (1/r3,1/r2, 1/r), а сплошной линией соответствует суммарная напряженность.

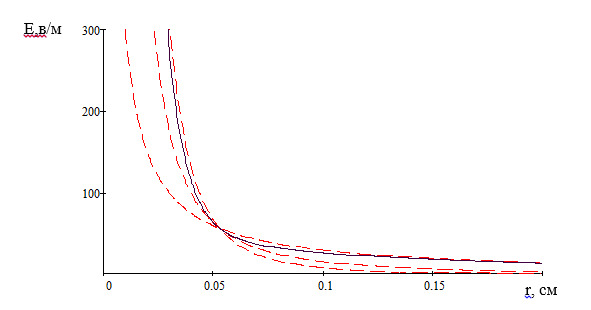
В дальней зоне влияние составляющих 1/r3,1/r2, сводится к минимуму и приближенно можно считать изменение поля по закону 1/r.

В практических измерениях определяется принадлежность точки измерения к зоне излучения.

Об измерении электромагнитных полей.

Для оценки защищенности ПЭМИ технических средств (ТС) в диапазоне 0,01- 1000Мгц приемник ЭМП (антенну) размещают на расстояниях один метр, что соответствует ближней и промежуточной зоны излучения от исследуемых средств. Как известно граница зон определяются условиями Rбз = λ/2π и Rпз = 6λ.

Определим принадлежность расчетного расстояния rрас. к одному из следующих интервалов (13.9).

Корректность использования антенн для проведения измерений определяется характером поля в ближней и промежуточной зонах, типом и характеристиками антенн. Ка, hд

Заключение о соответствия ПЭМИ ТС нормам проводится по соотношению с/ш (Ес/Eш) на границе контролируемой зоны.

О распределении поля.

Будем рассматривать поле, создаваемое элементарным электрическим (или магнитным) излучателем в какой-либо точке. Наиболее типичное излучение имеют электрические излучатели. Для этого случая в сферической системе координат дей­ствующие значения составляющих поля, указанные выше.

Распределение поля вблизи излучателя характеризуется отношением напряженностей электрической и магнитной составляющей, которые можно получить из выражений для Eθ и Hφ.

Для электрического излучателя в ближней и промежуточной зоне имеем: E/H=W0 (λ/2πr), в дальней зоне: E/H=W0. Для магнитного излучателя, используя литературные данные, имеем значения E и H,: E/H=W0 (2πr/λ).

Здесь (13.10) — волновое сопротивление в свободном пространстве.

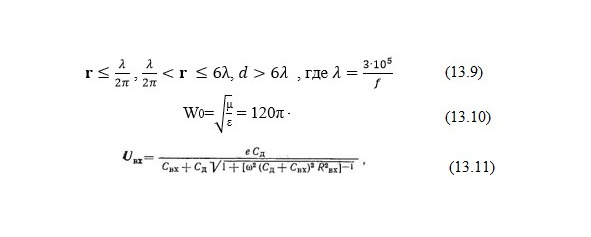
Из приведенных отношений видно, что в ближней зоне однозначной связи между электрической и магнитной составляющей нет. Поэтому для измерения электрической составляющей поля в ближней и промежуточной зоне нельзя использовать магнитные антенны, с целью пересчета значений H в E.

Об измерении полей в ближней зоне (зоне индукции).

Напряженность электромагнитного поля в БЗ и ПЗ значительно превосходят поля в волновой зоне; кроме того, они обла­дают значительной неоднородностью, усиливающейся наличием вблизи исследуемых ТС проводящими предметами, случайными антеннами и линиями коммуникаций. В силу этого в зоне индукции (в отличие от волновой зоны) нет определенной связи между компонентами электромагнитного поля, и поэтому невоз­можно по результатам измерения одной из них вычислить значе­ние второй. Из-за неоднородности поля в зоне индукции размеры измерительной антенны должны быть настолько малы, чтобы в области, занимаемой ею, поле можно было считать достаточно приближенным к однородному.

Для уменьшения погрешности вносимый в поле измеритель­ный прибор по возможности удаляют от измерительной антенны, основные элементы цепей измерителя (селективного вольтметра) помещают во внутренний экран, изолированный от корпуса прибора, входные цепи вольт­метра размещают в непосредственной близости от измерительной антенны, вход измерителя напряженности поля строго симметрируют по отношению к земле. На­рушение последнего требования может вызвать нежелательную разность потенциалов, наводимую большими полями, на входных клеммах прибора и так далее.

В качестве антенны для измерения электрическо­го поля применяется диполь, для измерения маг­нитного поля — рамка. С точки зре­ния конструкции и удобства обращения с измери­телем напряженности поля исследуем пассивную антенну, подключенную к входу селективного вольтметра или анализатора.

В теории приема и измерения характеристик электромагнитного поля часто используют эквивалентную схему, представленную на рис. 1, на которой Z А — полное входное сопротивление антенны; Zпр — полное входное сопротивление приемника; е — электродвижущая сила на выходе антенны

е = Е hд, где Е- напряженность электромагнитного поля, hд — действующая высота.

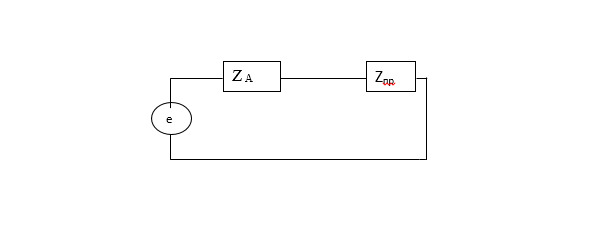
При согласованной нагрузки (оптимальный режим) Z А = Z ПР

Мощность и напряжение на входе приемника P, U.

На рис. 14 представлена эквивалент­ная схема входной цепей измерителей напряжен­ности поля с диполем. Схема простая, так как отсутствуют усилители, какие либо согласующие устройства, кабели.

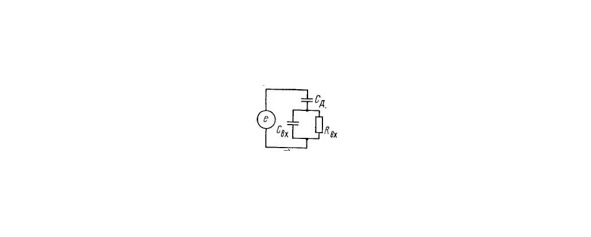
Для схемы (рис. 13) напряжение на входном сопротивлении вольтметра (13.11),

где е= EhД — эффективное значение ЭДС, наведенной полем в диполе, В;

Сд — собственная емкость диполя, Ф; RBX — активная составляющая входного сопротивления вольтметра, Ом; Свх — входная емкость вольтметра, Ф.

Из выражения для Uвх видно, что показания измерителя будут зависеть от час­тоты. Эта зависимость практически исключается, если величина ω2 (Сд+Свх) 2R2вх выбрана достаточно большой (что реализуется в активных антеннах). Для пассивного вибратора при низком входном сопротивлении измерителя (RBX =50 ом), малом значении Сд = 5 пф Uвх будет <<е. Это означает, что измерения нельзя проводить (практически трудно измерить).

Проведенные натурные измерения для различных приемников и антенн дают другую картину.

Уровни измерений Е имеют отклонения от показаний, полученных с использованием калиброванных активных и пассивных антенн, соизмеримые с погрешностью метода измерения ближнего поля.

Коэффициент калибровки стандартных антенн приведенных в паспортах на антенны для дальнего поля и согласованных с регламентированной нагрузкой.

Отклонения результатов измерений лежат в пределах нескольких дБ на различных частотах. Это говорит о коэффициенте согласования Kc диполя с входом селективного вольтметра. Эта связь выражается так.

Е =e /hд = Ка Uвх Kc

Коэффициент согласования для схем измерения имеет важное значение при проведении измерений, влияет на точность метода измерения в ближней и промежуточной зонах.

Действующая высота антенны hД

Связь между геометрической и действующей высо­той вертикального вибратора при la <<λ: hд=lа /2. Действующая высота четвертьволнового вибратора hд = λ/2π. Эти значения получены путем интегрирования косинусоидальной функции распределения тока штыревой антенны по ее физической высоте.

О коэффициенте калибровки.

Измерение Eс+п и Еп для оценки защищенности ПЭМИ проводится вблизи технического средства при размещении антенны или измерителя в следующих случаях.

а. рядом с ТС на фоне естественных помех

б. рядом с ТС при использование генераторов помех.

в. на границ КЗ на фоне естественных помех

г. на границе КЗ при использование генераторов помех.

д. для получения абсолютных значений напряженностей при использовании в расчетах нормируемых помех.

е. для определения реального коэффициента затухания Кр. з.

Для вариантов б,г,е измерения требуются для получения отношения сигнал шум q и определения реального коэффициента затухания Кр. з.

q= EсСП / EпСП = (Ка Uвхсп Кс) / (Ка Uп сп. Кс) = Uвх сп /Uп сп.

Кр. з.=Ес1/Ec кз = (Ка Uвх. с1 Кс) / (Ка Uс кз. Кс) = Uвх. с1 /Uс кз.

Как видно из полученного выражения результаты оценки q не зависят от коэффициента согласования и калибровки при линейности входного измерительного тракта в динамическом диапазоне сигнала.

Для вариантов а,в,д проводится измерения абсолютных величин, их усреднение оценки параметров измерения.

Антенны

В практике измерения ЭМП с целью оценки защиты информации в настоящее время используются антенны различных типов.

Антенны предназначены для измерения напряжённости электрического, магнитного и электромагнитного полей совместно с измерительными приёмными устройствами.

Антенны характеризуются назначением, частотным диапазоном, коэффициентом калибровки, и другими различными параметрами.

Рассмотрим особенности использования различных антенн для целей проверки эффективности защиты ПЭМИ.

1. Антенны бывают пассивными и активными.

О характеристиках пассивных антенн.

Сопоставим мощность принимаемых сигналов с полной мощностью различных шумов на входе приемника разведки.

Шумы антенн характеризуются внешними и внутренними шумами.

Внешние шумы антенн вызваны электромагнитными помехами естественного и техногенного происхождения.

Внутренние шумы антенн вызваны тепловым движением электронов в неидеальных проводниках и диэлектриках антенн и фидерном тракте.

Спектральный состав внешних и внутренних шумов для диапазонных антенн можно принять одинаковыми.

Полная мощность шума на входе приемника равна

Pш полн = Pш а + P ш. пр., где

Pш а = kTa D f, Вт — мощность шумов антенны, подводимая к приемнику.

Pш пр. = kTпр D f, Вт — мощность шумов приемника.

Шумовая температура антенн Та = Та ф.+ Та. S., где

Та ф. — флюктуационные шумы антенны.

Та. S. — температура внешних источников шумов.

Значение Та. ф. находится с использованием формулы Нейквиста для ЭДС и импенданса приемника Zвх.

Та. ф. = T0 (1-h).

Очевидно, что величина Та. ф. не превышает 288К, т.е. вклад пассивной антенны в Uвх. ш. мал.

Значение Та. S. определяется яркостной температурой в окружающем пространстве, атмосферными, индустриальными и космическим помехами радиоизлучением земли и др. Возможно уменьшения значения Та. S. за счет направленности пассивных антенн.

В диапазоне длинных, средних и КВ значения Та. S. значительно больше Та. ф.. (Та. S.>> Та. ф.).

В децеметровом и СВЧ диапазонах за счет направленности антенн значения Та. ф и. Та. S. соизмеримы или Та. S. <Та. ф.

Однако значение Та. S. <Та. ф. не относятся к индустриальным помехам, которые часто нельзя устранить направленными антеннами.

Достоинство пассивных антенн.

Динамический диапазон входного сигнала не ограничивается.

Шум антенны регламентируется внешним шумом.

Нижняя граница Uш а = Рша /ka

Динамический диапазон имеет линейную характеристику.

Недостатки пассивных антенн.

Малый коэффициент калибровки или коэффициент калибровки

Требуется иногда согласование антенны с приемником.

Требуется частотная корректировка коэффициент калибровка и из-за рассогласования

Активные антенны

Недостатки и требования активных антенн

Требуется электропитание на усилительные блоки.

Наличие мощных станций и помех и применение широкополосных усилителей вызывает создание перекрестных помех на входе измерительного приемника. Происходит нелинейное преобразование входных сигналов различных частот и появление помех.

Мгновенный динамический диапазон должен быть достаточно большим (порядка 120 дБ), что трудно реализовать в широком частотном диапазоне.

Мгновенный динамический диапазон должен быть линейным в исследуемом частотном диапазоне.

Преимущество активных антенн

Малые размеры антенны.

Повышена чувствительность измерительной системы.

Характеристики антенн

Коэффициент калибровки и действующая высота антенны.

Рассмотрим заземленный или несимметричный вибратор под которым понимают такой, который подключается к одному зажиму источника э. д. с., а другой зажим источника заземляется (рис.15). Заземленный вибратор в совокупности со своим зеркальным изображением образует симметричный вибратор.

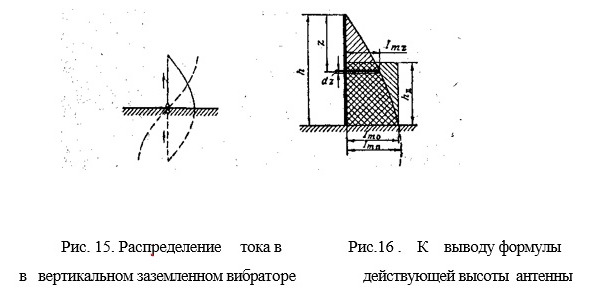
Поэтому диаграмма направленности заземленного вибратора представляет собой верхнюю поло­вину диаграммы направленности соответствующего симметричного вибратора. Отсюда следует также, что максимум излучения верти­кального заземленного вибратора при идеальной проводимости Земли находится на ее поверхности.

Для определения сопротивления излучения заземленного виб­ратора обратимся к рис. 15, на котором начало координат совпадает с вершиной вибратора, ось z направлена по оси вибратора,

1т z — амплитуда тока на расстоянии zот вершину вибратора.

1т п — амплитуда тока в пучности, 1т0 — амплитуда тока в осно­вании; антенны,

h — геометрическая высота вибратора, hд — его действующая высота.

Будем считать эквивалентными вибраторы, которые создают поле одинаковой напряженности в направлении максимального излучения антенны. В этом направлении отсутствует разность хода волн от симметричных элементов вибратора, вследствие чего результирующее поле равно алгебраической сумме полей всех элементарных участков вибратора, каждый из которых эквивалентен элементарному вибратору.

Амплитуда напряженности поля элементарного вибратора пропорциональна моменту тока, измеряемого в микроамперах. Следо­вательно, вибраторы являются эквивалентными, если равны их моменты токов.

В заземленном вибраторе, где ток распределяется неравномерно по высоте, момент тока равен интегралу

∫oh1т zdz

Если в качестве эквивалентного вибратора выбрать такой, в котором па всей высоте ток одинаков и равен току у основания заземленного вибратора 1т0, то к последнему можно применить формулы, выве­денные для элементарного вибратора. Высота эквивалентного вибратора называется действующей высотой истинного вибратора. Очевидно, что действующая высота вибратора hд меньше его гео­метрической высоты h.

Из условия равенства моментов тока действительной и экви­валентной антенн

Учитывая известные тригонометрические формулы (14.1 — 14.2) найдем (14.3).

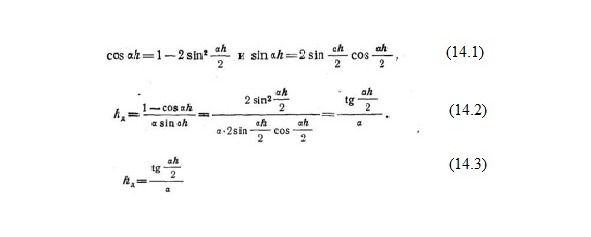
Формула для hд устанавливает связь между геометрической и действующей высо­той вертикального заземленного вибратора. Если h <<λ, то (14.4). Действующая высота четвертьволнового вибратора (14.5 — 14.6).

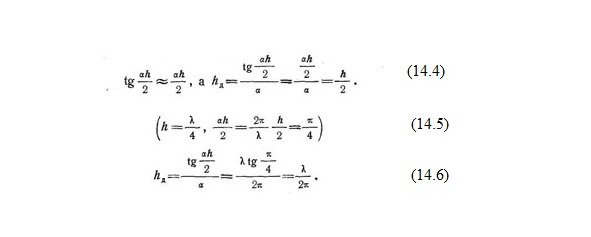
Так как в данном случае λ/2π =2h/π, то можно сказать, что увеличение геометрической высоты заземленного вибратора от весьма малой величины до λ/4 сопровождается увеличением его действующей высоты от 0,5 до 2/π=0,64 его геометрической высоты.

Заземленный вертикальный вибратор высотой h в совокупности со своим зеркальным изображением образует симметричныйвиб­ратор длиной l = 2h, а поэтому действующая высота симметрич­ного вибратора в 2 раза больше действующей высоты соответ­ствующего заземленного.

Следовательно, длина симметрич­ного вибратора hд= l/2 при 1 <<λ., а действующаявысота полуволнового вибратора hд= λ/π.

АНТЕННЫ ИЗМЕРИТЕЛЬНЫЕ

Основное назначение: измерение напряженности поля радиосигналов и радиопомех. Позволяют проводить измерения на испытательных площадках, в лабораториях и на локальных объектах. Могут быть использованы в составе автоматизированных измерительных комплексов. Приводится некоторые данные и характеристики антенн с опубликованного сайта в сети интернет.

1 АНТЕННА ФЕРРИТОВАЯ АФА-1

Полоса рабочих частот от 10 Гц до 100 кГц. Коэффициент калибровки антенны в рабочей полосе частот: не более 6 дБ (1/Ом·м).Неравномерность коэффициента калибровки не более 6 дБ. Погрешность определения коэффициента калибровки антенны — не более 2 дБ. Максимальное измеряемое значение: не менее 120 дБ (мкА/м). Возможна поставка антенны с переключаемым встроенным аттенюатором (для измерения полей большой напряженности).

2 АНТЕННА РАМОЧНАЯ АКТИВНАЯ АРА СР

Полоса рабочих частот 0,009 — 30 МГц. Диаметр приемных рамок 0,15 м; 0,3 м; 0,6 м. Коэффициент калибровки антенны в полосе рабочих частот: -10 дБ 1/Ом м; -18 дБ 1/Ом м; -25 дБ 1/Ом м. Неравномерность коэффициента калибровки антенны не более 6 дБ.

3 АНТЕННА ДИПОЛЬНАЯ АКТИВНАЯ АДА-1

Полоса рабочих частот от 30 Гц до 30 МГц. Антенна снабжена двумя парами сменных вибраторов длиной 0,1 и 0,25 м. Среднее значение коэффициента калибровки антенны в полосе рабочих частот не более: с вибраторами длиной 0,1 м — 36 дБ; с вибраторами длиной 0,25 м — 24 дБ. Неравномерность коэффициента калибровки антенны не более 6 дБ. Погрешность определения коэффициента калибровки антенны — не более 2 дБ

4 АНТЕННА ДИПОЛЬНАЯ АКТИВНАЯ АДА-2

Полоса рабочих частот от 9 кГц до 30 МГц. Антенна снабжена тремя парами сменных вибраторов длиной 0,1; 0,25 и 0.5 м. Среднее значение коэффициента калибровки антенны в полосе рабочих частот, дБ (1/м),дБ, не более: с вибраторами длиной 0,1 м — 36 дБ; с вибраторами длиной 0,25 м — 24дБ; с вибраторами длиной 0,5 м — 15 дБ. Неравномерность коэффициента калибровки антенны не более 6 дБ. Погрешность определения коэффициента калибровки антенны — не более 2 дБ.

5 АНТЕННА ДИПОЛЬНАЯ АКТИВНАЯ АДА-3

Полоса рабочих частот от 30 до 300 МГц. Длина съемного вибратора (диполя) 320 мм. Среднее значение коэффициента калибровки антенны в полосе рабочих частот: не более 25 дБ (1/м).Неравномерность коэффициента калибровки антенны не более 6 дБ. Погрешность определения коэффициента калибровки антенны — не более 2 дБ.

6 АНТЕННЫ БИКОНИЧЕСКИЕ

7 СИММЕТРИЧНЫЙ ВИБРАТОР

Является наиболее простейшим типом антенно-фидерных устройств, и представляет собой прямолинейный проводник, у которого в симметричных (относительно середины) точках токи равны по величине и имеют одинаковое направление в пространстве. На рис. 17. показан пример распределения тока, характерного для симметричного вибратора. Здесь в симметричных точках Z и -Z выполняется условие Iz=I-z. Стрелки на рисунке показывают, что токи в указанных симметричных точках имеют одинаковое направление. Естественно, что это направление показано для некоторого момента времени.

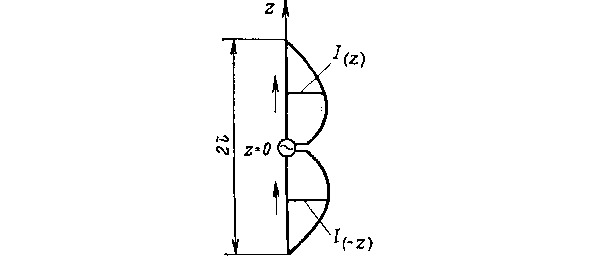
На рисунке ниже показаны диаграммы направленности симметричных вибраторов с разным соотношением L/l. Указанные фигуры представляют собой диаграммы направленности в плоскости, проходящей через ось вибратора. Пространственные диаграммы направленности представляют собой поверхности тел вращения, образуемых при вращении каждой кривой вокруг оси вибратора.