Бесплатный фрагмент - Исследование движения одиночной частицы в вертикальной трубе

Исследование движение одиночной частицы в вертикальной трубе.

Экспериментальные исследования по определению скорости витания частицы в вертикальном закрученном потоке проводились на лабораторной установке. Она состояла из вертикально установленной стеклянной трубы с внутренним диаметром 56 мм, длиной 3.0 м, к нижнему концу которой подсоединялись тангенциальные закручиватели 2 с формпараметрами 0.45; 0.81; 1.32. Установка (рис.3.19) работала по всасывающей схеме, производительность вентилятора 5 контролировалась измерительным блоком 4, показания которого дублировались термоанемометром ТА-1ОМ. В эксперименте использовалась сферическая гранула сульфата натрия δ=2,85 мм, G=0.02 г.

Опыты выполнялись в следующей последовательности. Устанавливался закручиватель с φ* = 0.45 и заслонкой в трубе 1 создавалась скорость равная скорости витания частицы в незакрученном потоке. Через отверстие 3 в восходящий поток вводилась частица, которая при установленной ранее скорости удерживалась между плоскостью ввода и верхней кромкой трубы. Затем заслонкой 6 постепенно снижалась скорость воздуха в трубе до тех пор, пока вращающаяся частица не опустится на высоту H=0/3м от закручивателя. При этом фиксировалась среднерасходная скорость, которая в данном случае имела величину 8.57 м/с. Далее плавно увеличивался расход воздуха до величины, при которой частица, обкатывая внутреннюю поверхность трубы, поднималась на следующую фиксированную высоту. Следует отметить, что вертикальный участок от 0.3 м до 0.5 м частица проходила за 5с, а затем скорость подъема резко снижалась и последующий участок она проходила за (50—60) с. Аналогично частица переводилась на высоту 1.0 м и 1.7 м, после чего устанавливался новый закручиватель и опыт повторялся. Результаты эксперимента приведены на рис.3.18.

Численный эксперимент проводился по двум моделям: с учетом либо только качения (по уравнениям (3.89)), либо только скольжения (по уравнениям (3.96)), по алгоритмам, отмеченным в предыдущих разделах. На рис.3.19 показаны изменения осевых скоростей частицы, рассчитанных по двум моделям. Важно отметить, что механизм движения частицы по первой модели принципиально отличается от эксперимента, где отсутствуют колебания осевой скорости частицы, а наблюдается только монотонное приближение частицы к равновесному положению (нулевой осевой скорости). Напротив, механизм движения частицы по второй модели адекватен экспериментальным наблюдениям. Следует также отметить, что зависимость высоты зависания частицы от параметров закрученного потока удовлетворительно согласуется с экспериментом. На рисунке 3.20 показано изменение высоты зависания частицы от тех же параметров, при которых проводился натурный эксперимент. Линии 1,2 и 3 построены по результатам численного эксперимента, но согласование с натурным получено при несколько отличных значениях формпараметра φ* (см. рис.3.20). Возможно, это связано с дефектами при изготовлении закручивателей, повлекших за собой отклонение истинного φ* от расчетного. Более подробно это явление рассматривается в гл.5.

Таким образом, проведенные исследования позволяют сделать вывод о том, что для разработки инженерных расчетов параметров транспортирования частиц в закрученных потоках может быть применена упрощенная модель в виде уравнений (3.96).

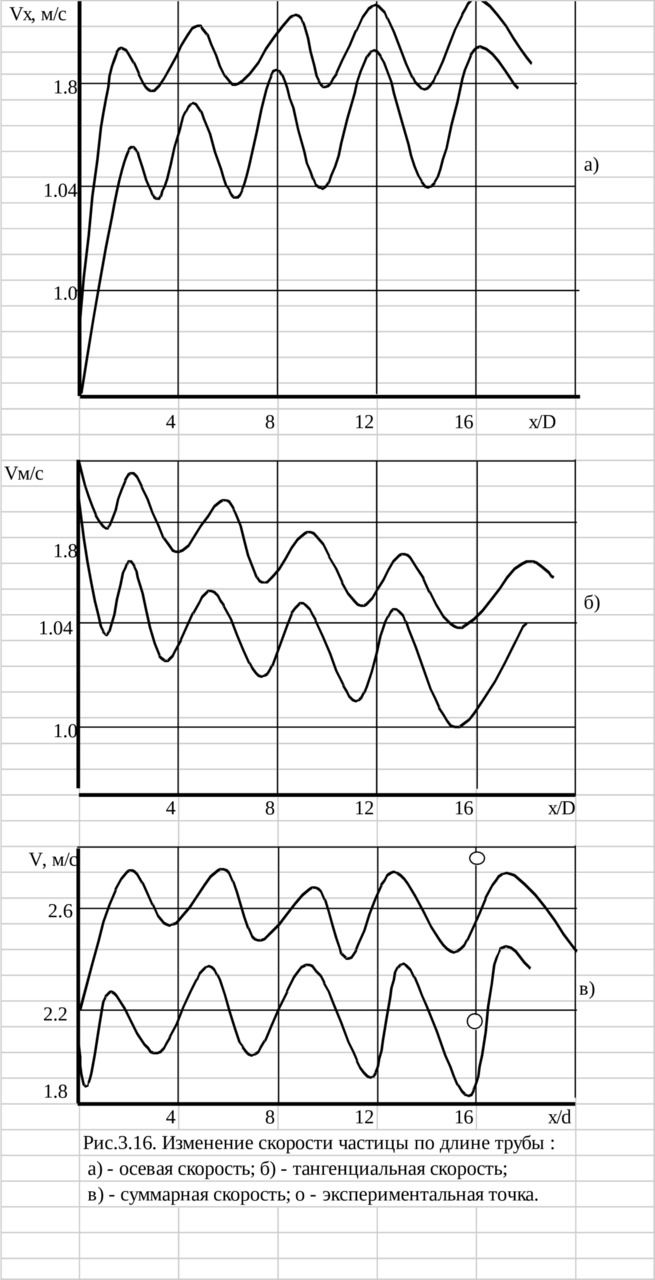
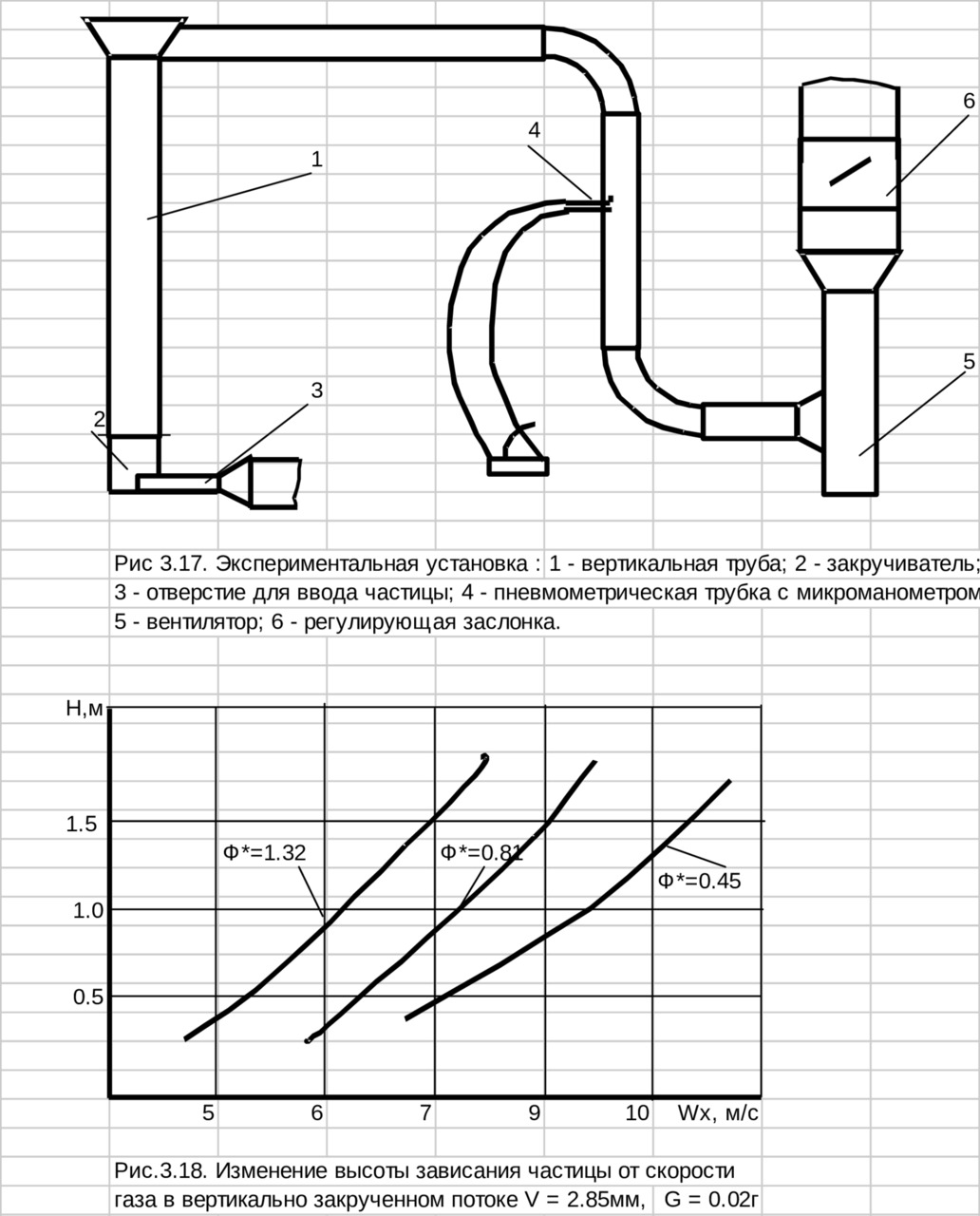
Рис 3.19. Изменение высоты подъема частицы от времени по результатам численного эксперимента: 1 — по уравнениям (3.96); 2 — по уравнениям (3.89); 3 — предельная высота зависания Xn. Условие эксперимента: {} ч = 1000 кг/м³; {} x = 10 м/с; D = 0.1м; {} * = 1; {} = 1мм; {} = 0.7.

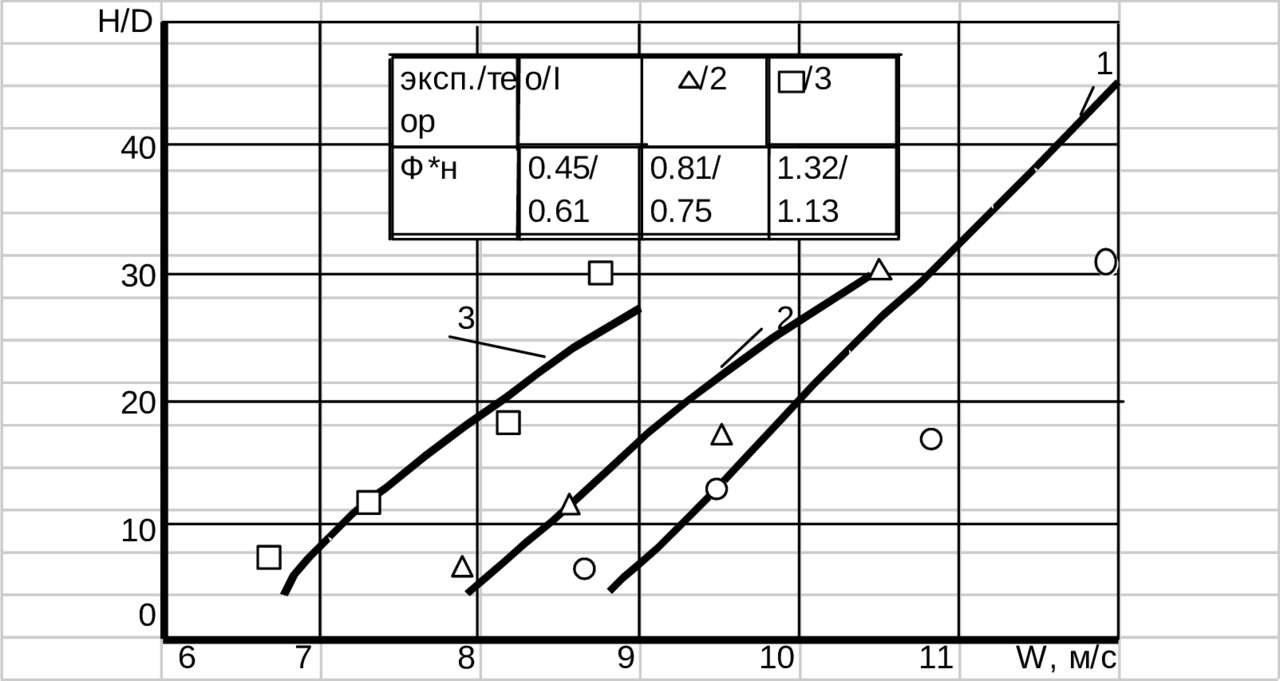
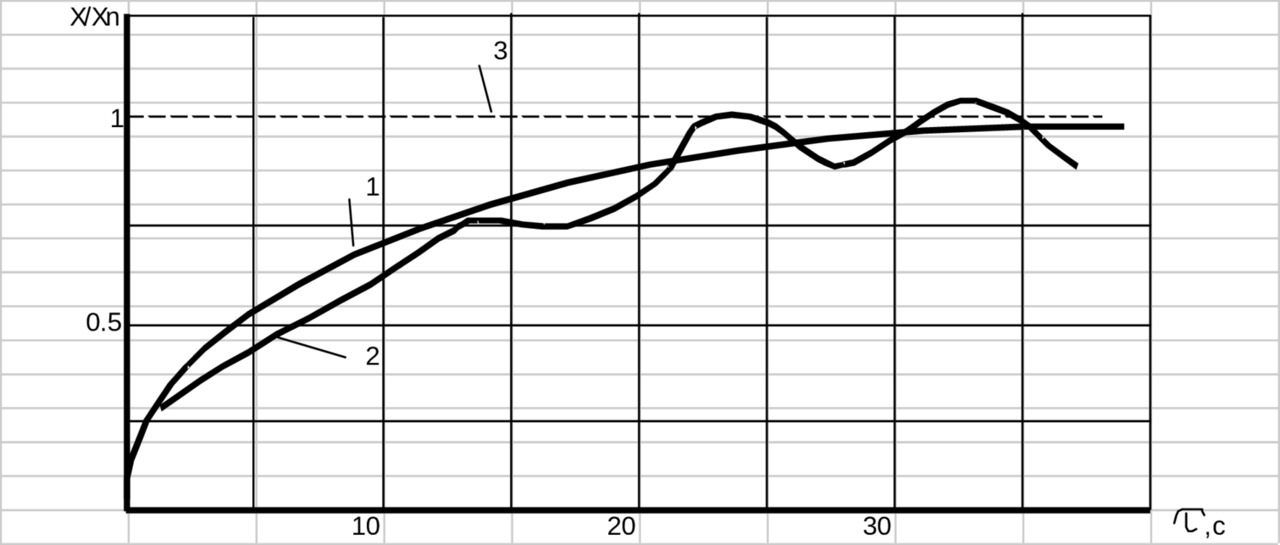
Рис.3.20. Изменение высоты зависания частицы от скорости газа в вертикальном закрученном потоке {} = 2.85; G = 0.02г. Численный эксперимент.

— Определение несущей скорости газа при транспортировании частиц вертикальном закрученном потоке.

Для практики представляет интерес определение минимальной скорости газового закрученного потока, способного транспортировать частицы на определенную высоту в вертикальной трубе.

Рассмотрим ситуацию, при которой частица будет равномерно обкатывать периметр трубы, находясь в динамическом равновесии. Определение всех сил, действующих на частицу требует знания ее тангенциальной скорости. Однако можно упростить задачу.

Рассмотрим две крайних ситуации в поведении частицы и выберем ту, которая дает искомую завышенную оценку несущей способности закрученного газового потока.

Крайние ситуации можно представить в виде: частицы движутся по периметру трубы и тангенциальные скорости частицы и газа равны; частицы упирается в препятствие и ее тангенциальная скорость равны нулю.

Тогда для первой ситуации условие равновесия частицы запишется в виде

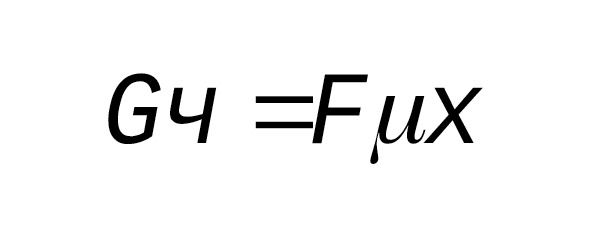
(3.99)

для второй

(3.100)