
Бесплатный фрагмент - Искусственный разум. Параллельная специализированная гибридная машина
Метод точного мгновенного решения NP задачи
Введение
В данной работе по возможности доступно, ясно мной излагаются основные понятия и функционирование параллельной специализированной гибридной вычислительной машины (МПСГВМ).
Главное внимание уделено общему представлению об операциях параллельной специализированной гибридной вычислительной машины при решении задач класса NP.
Функциональная схема параллельной специализированной гибридной вычислительной машины подчинена схеме метода точного мгновенного решения задач класса NP.
В данной работе предлагается эффективный безпереборный метод точного решения на МПСГВМ следующих комбинаторных оптимизационных задач:
• задача коммивояжера;
• задача Штейнера;
• задача о ранце;
• задача о назначениях;
• задача о назначении целей;
• задача теории расписаний;
• транспортная задача.
Этот метод мной разработан на примере задачи коммивояжера (ЗК), которая относится к классу NP и изложен мной в книге «Искусственный разум Задача коммивояжера Проблема перебора P=NP».
Данный метод вместо перебора осуществляет поиск оптимального решения на основе закономерности, присущей задачам класса NP.
Принципиальная новизна данной работы состоит в том, что она является первой и единственной, раскрывающей сущность почти мгновенного точного решения задач класса NP практически любого размера.
Модель параллельной специализированной гибридной вычислительной машины
Как известно, специализированные гибридные вычислительные машины предназначены для эффективного решения узкого класса задач.
К такому классу можно отнести и задачи класса NP комбинаторной оптимизации (КО). Комбинаторная оптимизация заключается в поиске оптимального решения в конечном множестве решений, то есть комбинаторные задачи можно решить методом полного перебора.
Во многих задачах КО полный перебор нереален. В настоящее время построение точных эффективных методов для так называемых труднорешаемых задач КО считается проблематичным и маловероятным.
К таким задачам относятся:
• задача коммивояжера;
• задача Штейнера;
• задача о ранце;
• задача о назначениях;
• задача о назначении целей;
• транспортная задача.
Доказано что они являются труднорешаемыми и относятся к классу NP. Для данного класса задач существующая проблема перебора в теории алгоритмов является открытой. Утверждается, что если будет решена эта проблема, то задачи класса NP можно будет решать с помощью одного единственного эффективного метода, так как эти задачи можно свести друг к другу.
В настоящее время разработанные точные методы решения задач КО являются, по сути, методами неявного перебора с экспоненциальной временной сложностью.
К ним относятся:
• метод ветвей и границ;
• метод динамического программирования.
Данные методы являются неэффективными по определению, так как требуют для решения задач КО экспоненциально зависящее от размера задачи время решения. Поэтому для решения задач КО разработаны приближённые эффективные методы.
К ним относятся:
• приближённые алгоритмы с гарантированными оценками качества получаемого решения;
• вероятностные алгоритмы.
В данной работе предлагается эффективный безпереборный метод точного решения комбинаторных оптимизационных задач.
Этот метод разработан на примере задачи коммивояжера (ЗК), которая относится к классу NP и изложен мной в книге «Искусственный разум Задача коммивояжера Проблема перебора P=NP».
Данный метод вместо перебора осуществляет поиск оптимального решения на основе закономерности, присущей задачам комбинаторной оптимизации (ЗКО).
Задача о ранце
Введение
Задача о ранце одна из труднорешаемых задач дискретной математики.
Название своё получила от максимизационной задачи укладки как можно большего числа ценных вещей в ранец при условии, что общий вес (или объём) всех предметов способных поместиться в ранец, ограничен.
Следовательно, эта задача является двухкритериальной.
На первом этапе решения необходимо найти множество подмножеств грузов с максимальной мощностью числа ценных вещей помещаемых в рюкзак, с учётом ограничения для ранца по весу W, а затем выявить максимальную суммарную ценность грузов в результате перебора конечного числа этих подмножеств с целью получить глобальное оптимальное решение.
На втором этапе решения нужно определить локальный оптимум решения задачи о ранце, уменьшая мощность подмножеств грузов.
В настоящее время не найдено эффективного метода точного решения задачи о ранце.
Постановка задачи о ранце
Пусть для задачи о ранце имеется n грузов. Для каждого i-го груза определён вес и ценность p,. Дана грузоподъёмность W.
Необходимо выбрать подмножество грузов максимальной мощностью, так чтобы их общий вес не превышал W, а суммарная их ценность была бы максимальной.
Метод решения задачи о ранце
Принимаем в качестве числа угадывания (Nуг) определённое числа грузов и объединений грузов различной мощности.
Предварительно необходимо выбрать подмножества грузов с максимальной мощностью М, так чтобы их общий вес не превышал W, путём выбора М грузов с минимальным их весом, и запомнить это число.
Первоначально осуществляется объединение и упорядочение по весу подмножества грузов по два. В дальнейшем проводиться поэтапное объединение грузов в конечные подмножества грузов, с увеличением мощности подмножества с упорядочением этих подмножеств по возрастанию веса, до получения множества грузов мощностью М по различным правилам.
Конечные подмножества проверяются по суммарному весу, которые не должны превышать W. Осуществляется итерационное угадывание количества этих подмножеств с различной мощностью, с последующей проверкой возможности выбрать подмножество грузов мощностью М, так чтобы их общий вес не превышал W.
После выявления множества подмножества грузов мощностью М с суммарным весом грузов меньше или равно W., с помощью данного метода, находится среди этого конечного множества искомый результат решения задачи о ранце в виде подмножество грузов, суммарная ценность которого была бы максимальной.
В результате поиска, согласно данного метода путём увеличения значения Nуг, после получении первого подмножества с мощностью М суммарным весом грузов больше W, процесс поиска заканчивается. Затем осуществляется выбор локального оптимума решения задачи о ранце с мощностью меньше М, путём уменьшения значения М и выбора Nуг.
Индикатором нахождения оптимального решения является само появление первого подмножества с суммарным весом грузов больше или равно W.
Для данного метода существует зависимость, согласно закономерности, присущей задачам комбинаторной оптимизации, которая является объективной.
В общем виде её можно представить в виде положительного градиента со сдвигом относительно начала координат.
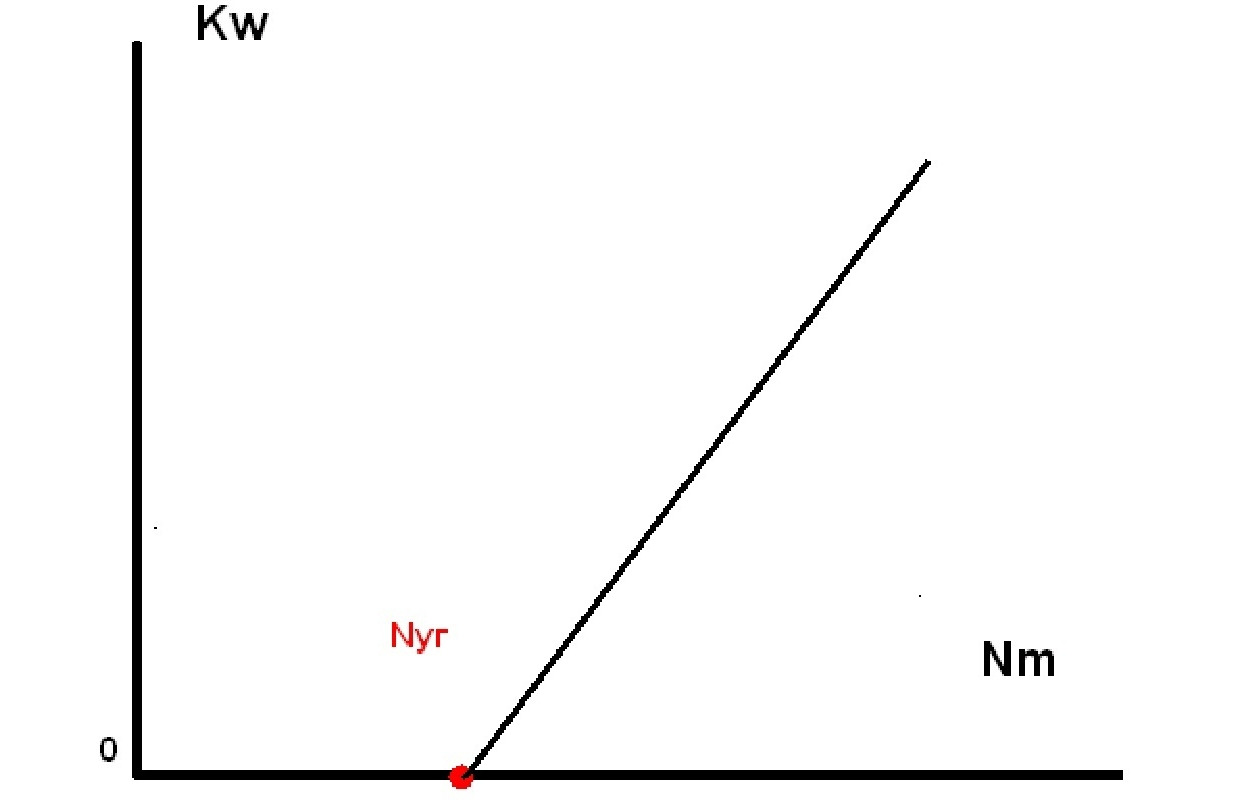
Где Кw — количество подмножеств мощностью М с суммарным весом грузов больше или равно W, Nm- шкала количества подмножеств грузов мощностью М, а Nуг — количество угаданных подмножеств грузов.
Метод включает:
1) выбор множества грузов с максимальной мощностью М, так чтобы их общий вес не превышал W, путём выбора грузов М с минимальным весом;
2) упорядочение множества грузов по возрастанию веса;
3) объединения грузов в подмножества грузов по два с последующим упорядочением и выбором этих подмножеств грузов с их наилучшими суммарными весами и соответствующей суммарной ценой согласно Nуг;
4) поэтапное объединение подмножества грузов меньшей мощностью грузов в подмножества грузов большей мощностью с последующим упорядочением до получения подмножеств грузов с числом грузов (М+1)/2 для М нечетных и с числом грузов М/2 +1 для М чётных и выбором, в дальнейшем, множества грузов подмножеств грузов большей мощности с их наилучшими суммарными весами и соответствующей суммарной ценой согласно Nуг.;
5) итерационный поиск подмножества грузов с числом грузов М с суммарным весом грузов больше или равно W;
6) выбор из множества подмножеств с максимальной мощностью М, подмножества, с суммарным весом грузов меньше или равно W, суммарная ценность грузов в котором была бы максимальной, путём перебора конечного числа этих подмножеств, т.е. получение искомого результата;
7) выбор локального оптимума решения задачи о ранце путём уменьшения значения М и выбора Nуг.
Алгоритм решения задачи о ранце
Шаг 1) Выбор подмножества грузов с максимальной мощностью М, так чтобы их общий вес не превосходил W, путём выбора М грузов с минимальным весом и запоминание его значения т.е. запоминание этого числа.
Шаг 2) Производится сортировка и запоминание грузов в соответствии с их весом, а также запоминается ценность этих грузов.
Шаг 3) Выбирается значение Nуг, и запоминается…
Шаг 4) Выбирается множество грузов с мощностью согласно Nуг с соответствующими им наилучшими весами и ценами.
Шаг 5) Производится объединения грузов в подмножества грузов по два. Осуществляется запоминание этих подмножеств грузов, с учётом их весов и цен.
Шаг 6) Производится сортировка и запоминание подмножеств грузов по два с соответствующими им наилучшими весами и соответствующей суммарной ценой.
Шаг 7) Выбирается множество подмножеств грузов по два с мощностью согласно Nуг с соответствующими им наилучшими суммарными весами и соответствующей суммарной ценой.
Шаг 8) Производится объединения грузов по два в подмножества грузов по три и запоминание этих подмножеств, с их суммарным весом и соответствующей суммарной ценой показанное на рис.10. Осуществляется проверка суммарного веса подмножеств грузов по три. Подмножества грузов по три с суммарным весом больше W не рассматриваются.
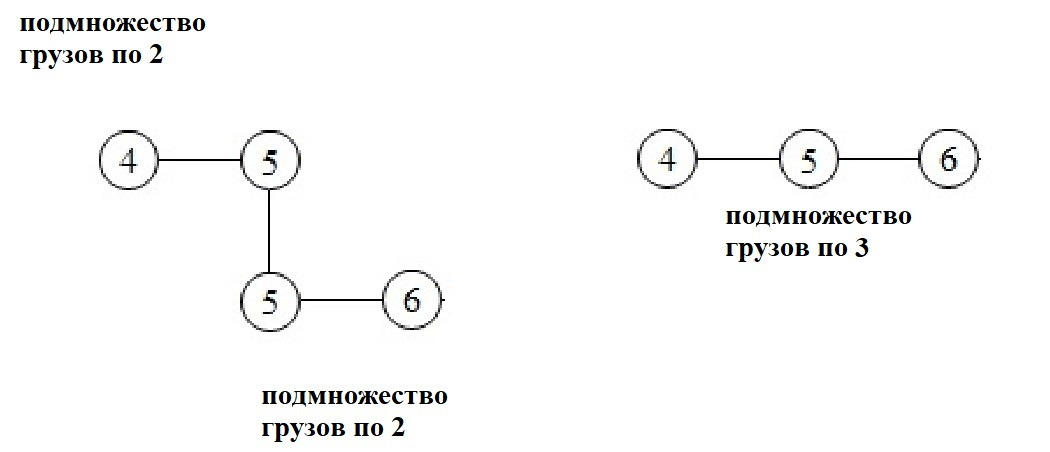
Данная процедура объединения подмножеств грузов меньшей мощности в подмножества грузов большей мощности, по различным правилам, должна повторятся до получения подмножеств грузов с числом грузов m = (М+1)/2 для M нечётных и с числом грузов m = M/2+1 для M чётных (пример объединения показан на рис. 4.12.). Где M максимальная мощность подмножества грузов в непустом множестве подмножеств грузов с общим весом меньше или равно W. Подмножества грузов большей мощности с суммарным весом больше W не рассматриваются. После каждого объединения, производится сортировка подмножеств грузов большей мощности в соответствии с их наилучшими суммарными весами и запоминание этих подмножеств грузов большей мощности с их суммарными весами и соответствующей суммарной ценой, а затем выбор подмножеств грузов большей мощности с их наилучшими суммарными весами и соответствующей суммарной ценой согласно Nуг. Если множество подмножеств грузов большей мощности в результате объединения на каком-то этапе данного объединения будет пусто то увеличиваем Nуг на определённое значение и запоминаем. Переходим к шагу 3. Если в результате объединения подмножеств грузов большей мощности будет равно и это множество этих подмножеств грузов будет не пусто, то переходим к шагу 9.
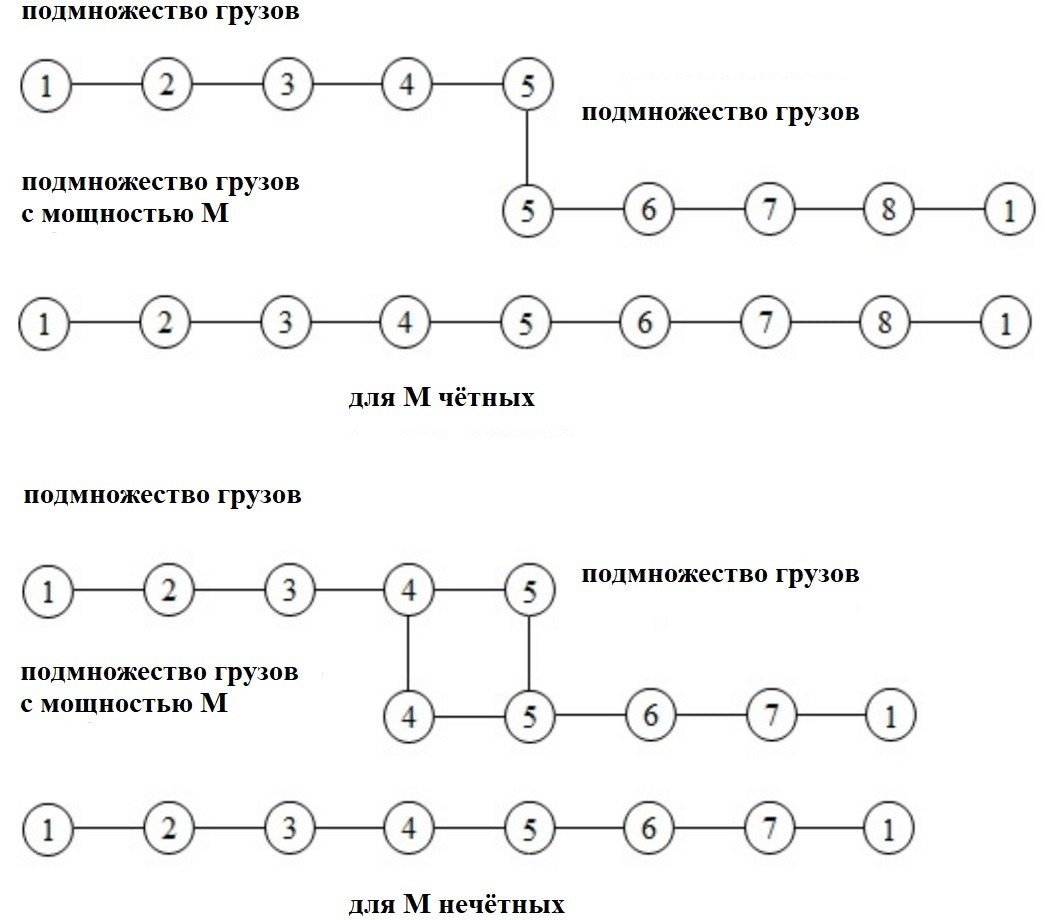
Шаг 9) В полученном множестве подмножеств грузов большей мощности числом грузов равным осуществляем их объединение, для получения множества подмножеств грузов мощности М. Если множества подмножеств грузов мощности М будет пусто то увеличиваем Nуг на определённое значение и запоминаем. Переходим к шагу 3. Если в результате объединение получим не пустое множество грузов мощности М, то выбираем из полученного множества подмножество грузов мощности М с суммарным весом грузов больше W. Если такое подмножество грузов мощности М, с суммарным весом грузов больше или равно W, будет не найдено то увеличиваем Nуг на определённое значение и запоминаем. Переходим к шагу 3. Иначе выбираем из полученного множества подмножеств грузов мощности М подмножество грузов с суммарным весом грузов меньше или равно W и с максимальной суммарной ценой, которое и будет искомым решением задачи о ранце.
Шаг 10) Уменьшаем значение М на 1, выбираем Nуг, и запоминаем. Если М> 0 то переходим к шагу 3. Иначе переходим к шагу11.
Шаг 11) Выбираем, из полученного множества локальных подмножество грузов с максимальной суммарной ценой для различных уменьшенных значений М, подмножество грузов с максимальной суммарной ценой, который и будет локальным оптимумом решения задачи о ранце.
Индикатором нахождения искомого результата является само появление такого подмножества грузов мощности М, суммарный вес грузов которого будет больше или равен W.
Демонстрационный пример решения задачи о ранце
Для задачи о ранце определим, что ранец имеет грузоподъёмность W = 12. Количество грузов n = 5. Значения весов грузов W зададим в виде таблицы 3.
Таблица 3. Определение весов грузов
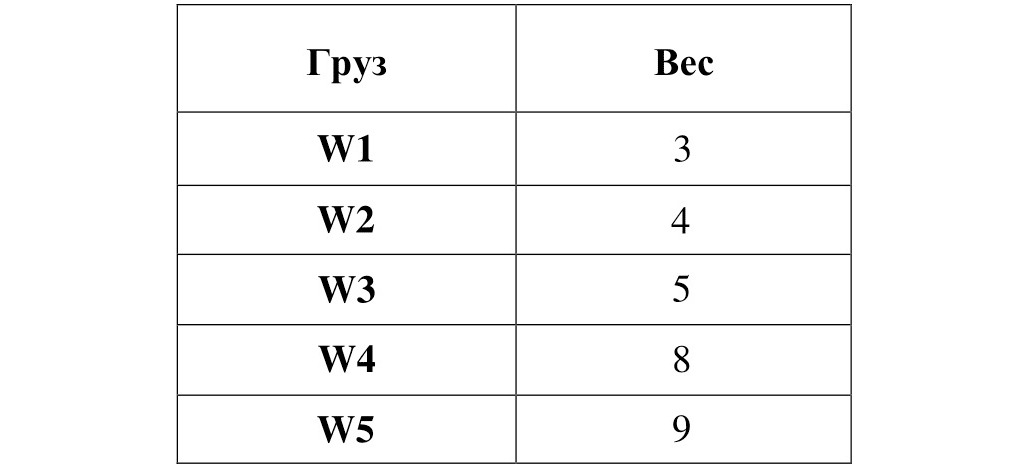
Для данного множества грузов максимальная мощность подмножеств грузов М = 3.
Согласно моего метода, для получения оптимального решения задачи о ранце, необходимо чтобы:
m = (М+1) /2 для M для нечётных;
m = M/2+1 для M для чётных.
Для данного примера задачи о ранце: М = 3, m = 2.
Значения цены грузов P зададим в виде таблицы 4.
Таблица 4. Определение цены грузов
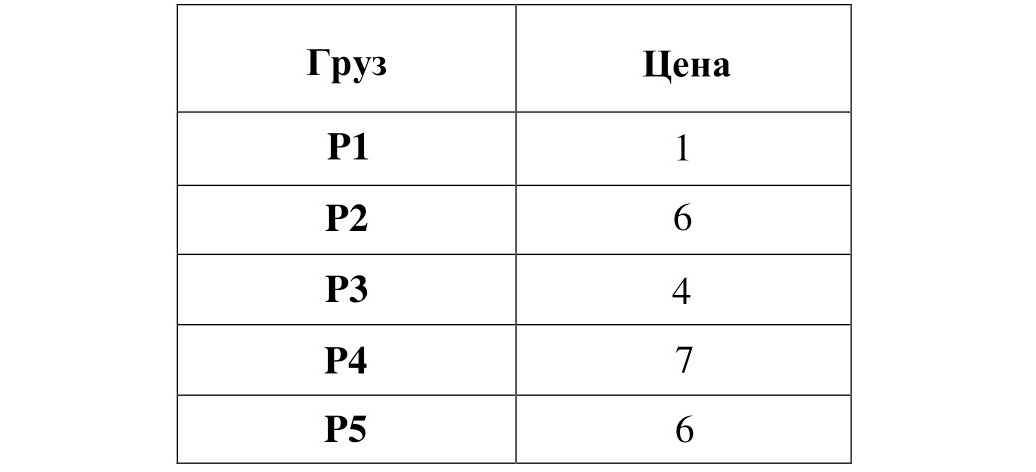
С помощью метода неявного перебора был получен оптимальный результат для данного примера задачи о ранце:
W = W2 + W4 = 4 + 8 = 12
P = P2 + P4 = 6 + 7 = 13
Занесём определённый упорядоченный вектор грузов относительно значений весов грузов и их цены в таблицу 5.
Произведём объединение грузов из множества грузов в подмножества грузов по два и по три.
Полученные упорядоченные вектора подмножества грузов по два и по три и их значений суммарных весов грузов и цен занесём в таблицу 5.
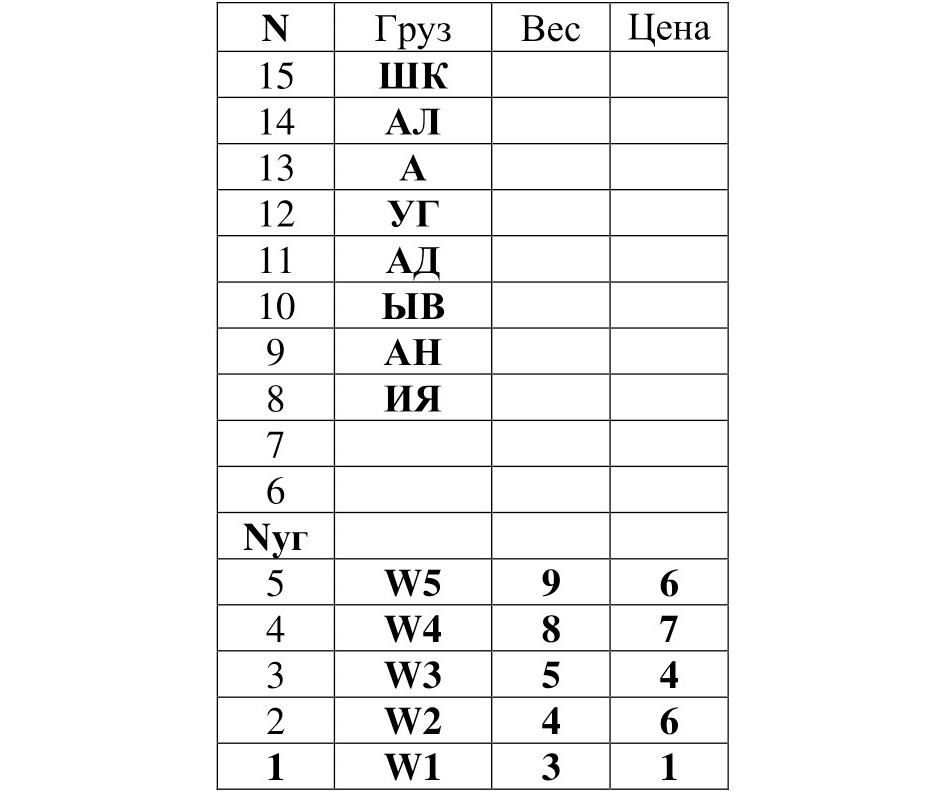
Таблица 5. Определённый и полученные упорядоченные вектора грузов
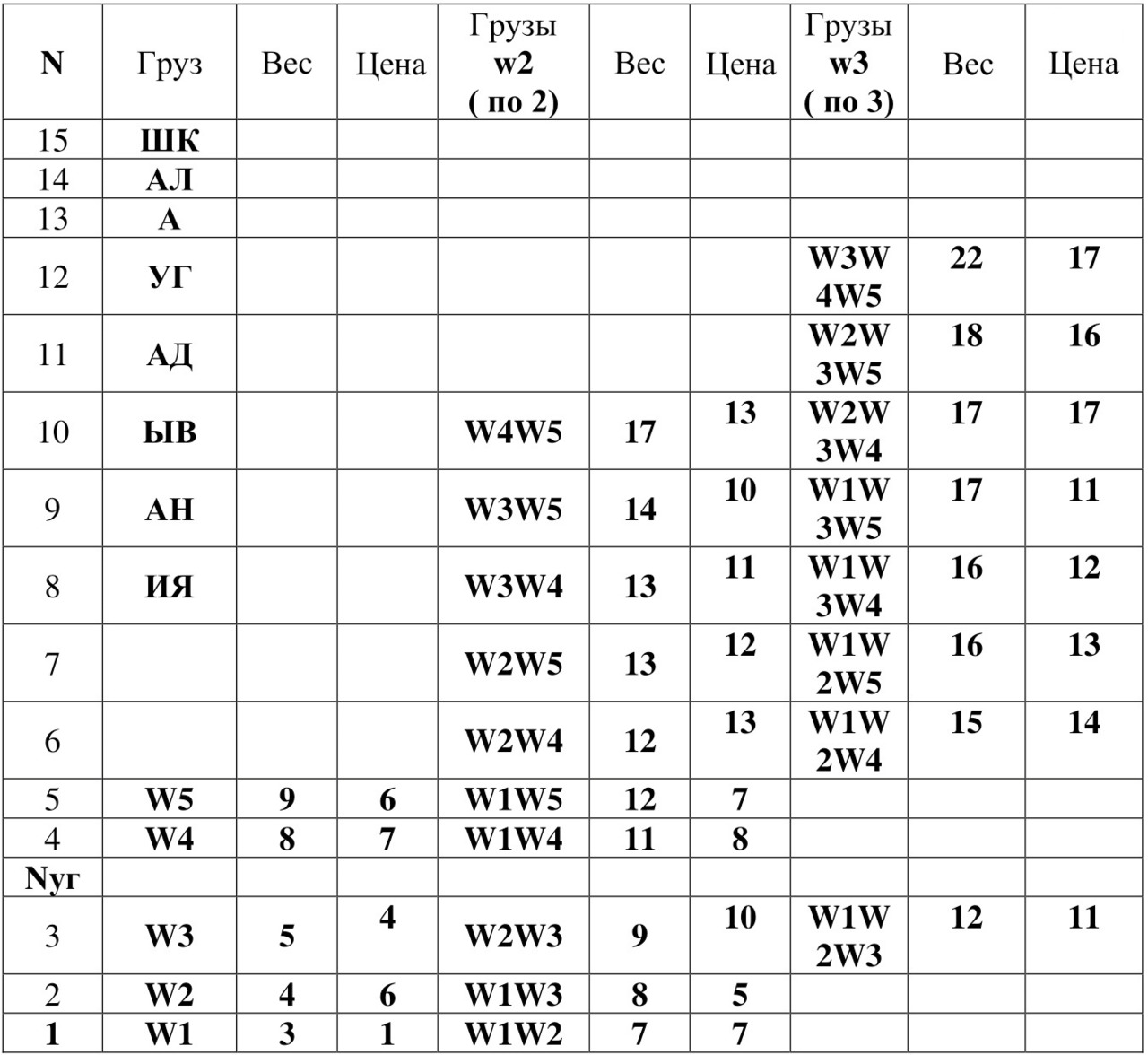
Из таблицы 5 видно, что для определения глобального оптимального результата в данном примере задачи о ранце: для данного метода достаточно чтобы Nуг = 3. Искомый результат:
W = W1 + W2 + W3 = 3 + 4 + 5 = 12
P = P1 + P2 + P3 = 1 + 6 + 4 = 11
Таким образом, без перебора вариантов решения задачи о ранце, находим данным методом глобальный оптимальный результат данного примера задачи о ранце.
Основываясь на данных из таблицы, определим зависимость числа подмножеств по три (Kw3) с суммарным весом грузов больше или равно W = 12, от числа угадывания (N) на шкале угадывания (Nm) для данного метода.
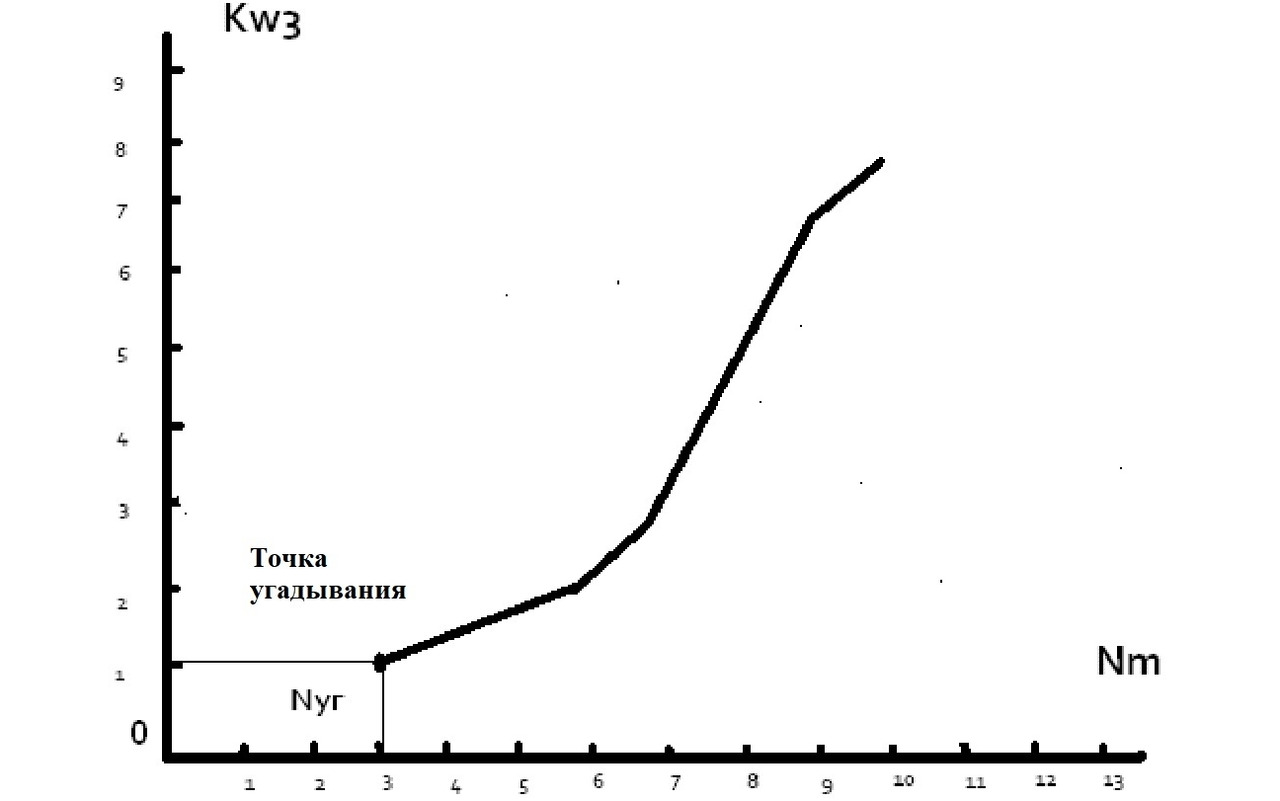
Где Кw3 — количество подмножеств грузов по три, с суммарным весом грузов больше или равно W.
Nm — шкала угадывания количества подмножеств грузов.
Nуг — количество угаданных подмножеств грузов.
Согласно данного метода определим локальное оптимальное решения задачи о ранце для значений:
М = 2 и Nуг = 4.
Рассмотрим таблицу 6 для значений М = 2 и Nуг = 4.
Таблица 6. Определённый и полученный упорядоченный вектор грузов для М = 2 и Nуг = 4.
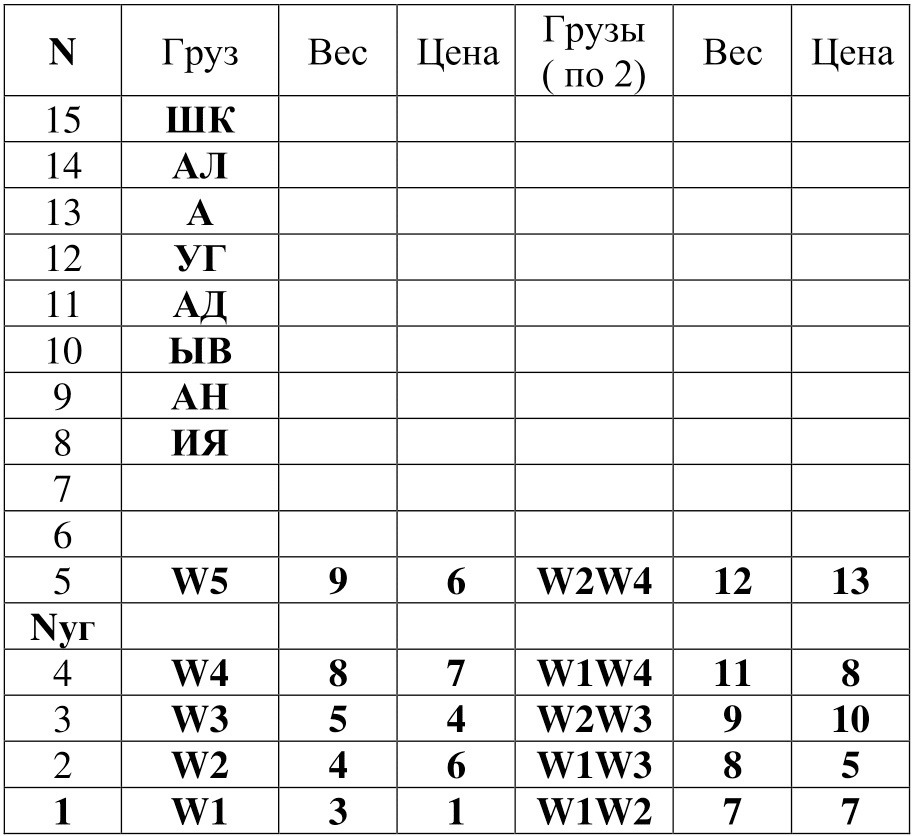
Из таблицы 6 определим локальное оптимальное решения задачи о ранце:
W = W2 + W4 = 4 + 8 = 12
P = P2 + P4 = 6 + 7 = 13
Согласно метода, определим локальное оптимальное решения задачи о ранце для значений М = 1 и Nуг = 5 согласно таблицы 7.
Таблица 7. Определённый вектор грузов для
М = 1 и Nуг = 5
Из таблицы 7 определим локальное оптимальное решения задачи о ранце для М = 1 и Nуг = 5 :
W = W4 = 8
P = P4 = 7
Исходя из вышеизложенного выбираем локальный оптимальный результат данного примера задачи о ранце:
W = W2 + W4 = 4 +8 = 12
P = P2 + P4 = 6 + 7 = 13.
Таким образом, без перебора вариантов решения задачи о ранце, находим данным методом локальный оптимальный результат и глобальный оптимального результат для данного примера задачи о ранце с помощью моего метода. Определение лучшего результата требует выполнение дополнительных условий. Необходимо определить, что для нас является более важным, число грузов или их ценность.
Что и требовалось доказать.
Задача о назначениях
Введение
Задача о назначениях — одна из фундаментальных задач комбинаторной оптимизации. Задача состоит в поиске минимальной суммы дуг во взвешенном двудольном графе.
В наиболее общей форме задача формулируется следующим образом:
Имеется некоторое число работ и некоторое число исполнителей. Любой исполнитель может быть назначен на выполнение любой одной работы, но с неодинаковыми затратами. Нужно распределить работы так чтобы выполнить работы с минимальными затратами.
В настоящее время неизвестен эффективный точный метод решения задачи о назначениях.
Постановка задачи
Для задачи о назначениях даны два множества А и Т одного размера и задана функция стоимости
С: А × Т → R
Необходимо найти биекцию ƒ: А → Т такую, что целевая функция
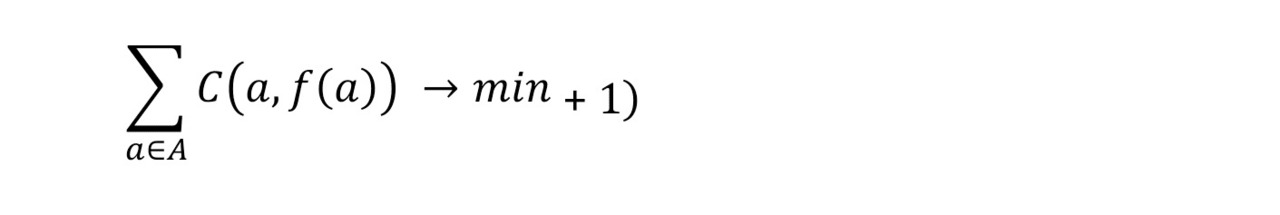
Метод решения задачи о назначениях
Определяется в качестве числа угадывания (Nуг) определённое числа исполнителей и подмножеств исполнителей различной мощностью.
Первоначально осуществляется объединение исполнителей по два и упорядочение по затратам подмножеств исполнителей. В дальнейшем проводиться поэтапное объединение исполнителей в конечные подмножества исполнителей, с увеличением мощности подмножества с упорядочением этих подмножеств по возрастанию затрат, до получения подмножества исполнителей мощностью m, где
m = (М+1)/2 для нечётной мощности множества исполнителей (M) и
m = M/2+1 для M чётных.
Осуществляется итерационное угадывание количества этих подмножеств с различной мощностью.
В результате поиска, согласно данного метода путём увеличения значения Nуг, после получении первого подмножества с мощностью М процесс поиска заканчивается.
Индикатором нахождения оптимального решения является само появление первого подмножества исполнителей мощностью М.
Для данного метода существует зависимость, согласно закономерности, присущей задачам комбинаторной оптимизации, которая является объективной.
В общем виде её можно представить в виде положительного градиента со сдвигом относительно начала координат.
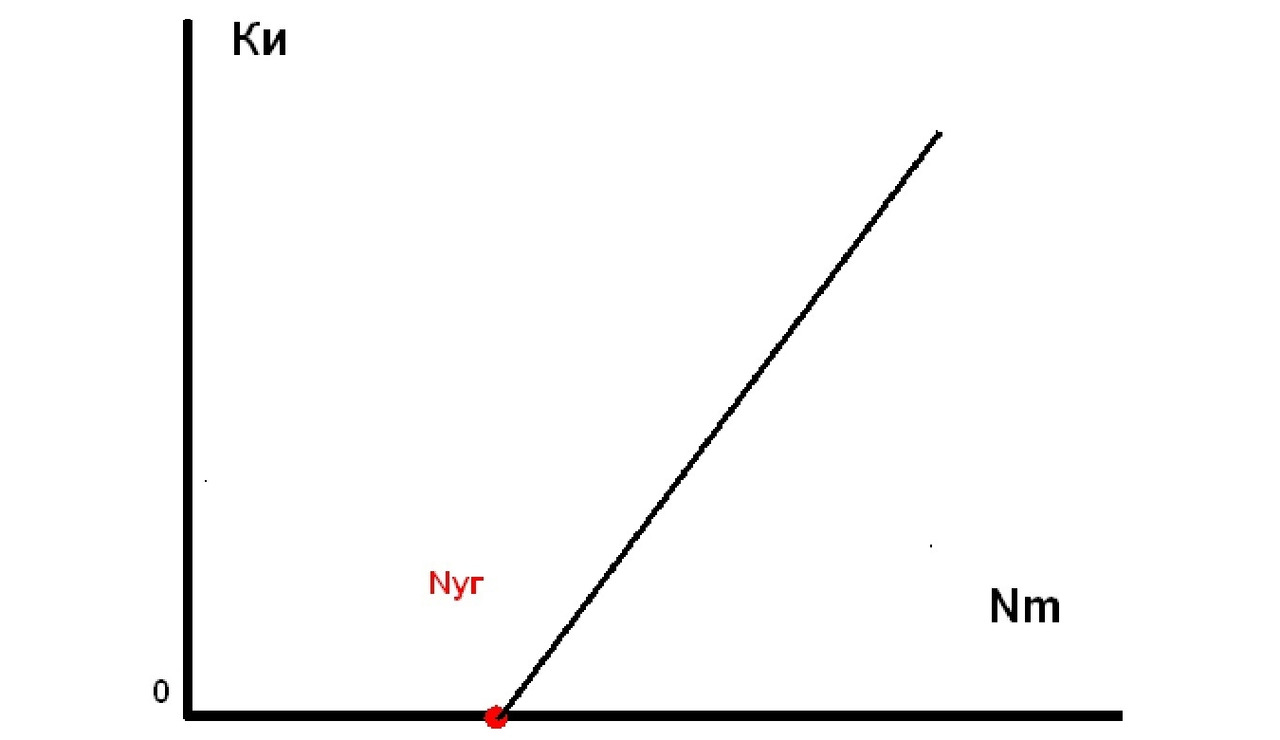
Где Ки — количество подмножеств исполнителей для всех работ, Nm — количество подмножеств исполнителей а Nуг — количество угаданных подмножеств исполнителей.
Алгоритм решения задачи о назначениях
Шаг 1) Определяем в качестве числа угадывания (Nуг) определённое числа исполнителей и подмножеств исполнителей различной мощностью.
Шаг 2) Производится сортировка и запоминание исполнителей в соответствии с их затратами.
Шаг 3) Выбирается значение Nуг, и запоминается…
Шаг 4) Выбирается множество исполнителей с мощностью согласно Nуг с соответствующими им наилучшими затратами.
Шаг 5) Производится объединения исполнителей в подмножества исполнителей по два и запоминание этих подмножеств исполнителей, с учётом их затрат.
Шаг 6) Осуществляется сортировка и запоминание подмножеств исполнителей по два с соответствующими им наименьшими затратами.
Шаг 7) Выбирается множество подмножеств исполнителей по два с мощностью согласно Nуг с соответствующими им наименьшими затратами
Шаг 8) Производится объединения исполнителей по два в подмножества исполнителей по три и запоминание этих подмножеств с их наименьшими затратами.
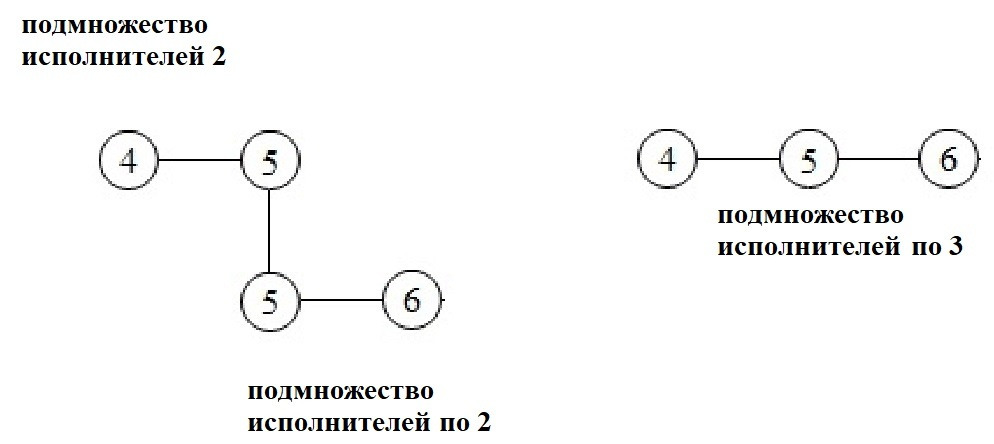
Данная процедура объединения подмножеств исполнителей меньшей мощности в подмножества исполнителей большей мощности, по различным правилам, должна повторятся до получения подмножеств исполнителей с числом исполнителей m = (М+1) /2 для М нечётных и с числом исполнителей m = M/2+1 для M чётных (пример объединения исполнителей в подмножество показан на рис.4.17.), где М является мощностью множества исполнителей.
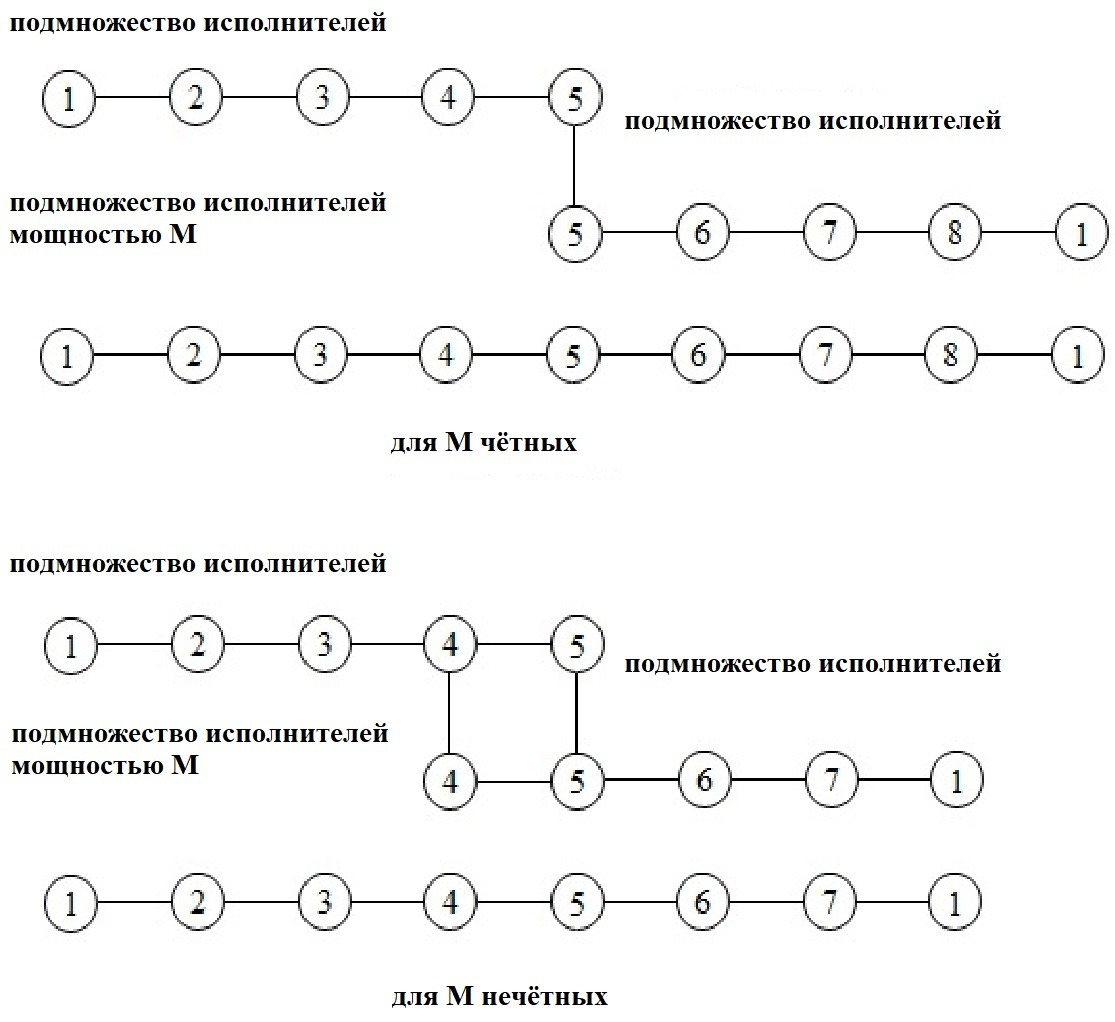
После каждого объединения, производится сортировка подмножеств исполнителей большей мощности в соответствии с их наименьшими затратами и запоминание этих подмножеств исполнителей большей мощности с их затратами, а затем выбор подмножеств исполнителей большей мощности с их наименьшими затратами согласно Nуг. Если множество подмножеств исполнителей большей мощности в результате объединения на каком-то этапе данного объединения будет пусто то увеличиваем Nуг на определённое значение и запоминаем. Переходим к шагу 3. Если в результате объединения подмножеств исполнителей большей мощности будет равно m и это множество этих подмножеств исполнителей будет не пусто, то переходим к шагу 9.
Шаг 9) В полученном множестве подмножеств исполнителей большей мощности числом исполнителей равным осуществляем объединение, для получения множества подмножеств исполнителей мощности М. Если множества подмножеств исполнителей мощности М будет пусто то увеличиваем Nуг на определённое значение и запоминаем. Переходим к шагу 3. Если а результате объединение получим не пустое множество исполнителей мощности М, то выбираем из полученного множества подмножество исполнителей мощности М подмножество исполнителей с суммарными наименьшими затратами, которое и будет искомым решением задачи о назначениях.
Индикатором нахождения искомого результата является само появление такого подмножества исполнителей мощности М.
Демонстрационный пример решения задачи о назначениях
Для задачи о назначении определим значения затрат исполнителей на выполнение определённых работ и зададим их в виде таблицы 8.
Таблица 8. Определение затрат исполнителей на выполнение определённых работ
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.