
Бесплатный фрагмент - Heron’s Triangles and Resonance Decays in Lobachevsky Velocity Space
Abstract
The ends of the velocity vectors of the decay resonance particles are represented by material points of the velocity pace located inside a sphere of radius C (C is the speed of light, the points are assigned the rest masses of the decay particles). The Lorentz group defines in the velocity space the Lobachevsky geometry of curvature k = -1/ C2. A pair of material points of 2-part resonance decay can be connected by a straight line segment and an arc of zero curvature line, called an oricycle [7]. Archimedes’ laws of levers define a 3rd velocity point “m” on the oricycle arc, in which the role of the lever forces is played by the rest masses of the decay particles, and the lever arms are equal to the oricycle arcs. Thus, to the two points with rest masses mπ, a 3-rd velocity point “m” with an additive mass ( mπ+ mπ) is added. Connecting 3 points with straight line segments, we obtain an isosceles triangle Δπmπ of the resonance decay inscribed in the oricycle. In the triangle Δπmπ the golden ratio is discovered and the Stewart and Bretschneider theorems are fulfilled on the arcs of the oricycle (see Appendix). The length of the base of the triangle Δπmπ of the resonance decay is determined by its effective mass.
Near the decay triangles of scalar, strange mesons and Δ, N baryons, satellite triangles with integer values of characteristics were discovered. Namely, for the satellite triangles, the function – the product of the length of the arc of the oricycle subtending their bases, multiplied by the cotangent of half the angle at the vertex opposite the base, takes on integer values. The function is called the oricyclic cotangent of a triangle (OCT) (see Tables 1–4). From Tables 1–4 it is clear that in addition to integer values of OCT, the sum of the hyperbolic cosines of the side lengths and the hyperbolic cosines of the base lengths of the satellite triangles are integers. Therefore, the satellite triangles are called Heron’s resonant triangles.Also in Tables 1–4 are given the obtained multiples of ½ values of the cosines of the angles between the tangent to the velocity point of the base of the Heron’s resonant triangles and the tangent to the velocity point of the additive mass (the values of the cosines > 1 mean that these tangents intersect outside the Absolute and the hyperbolic cosines of the lengths of the segments corresponding to such an angle are calculated).
Thus, the Heron’s resonant decay triangles determine the rigid structure of integers on the infinite radius of the oricycle. When moving along it to the center of the oricycle, new Heron’s resonant triangles with large integer values of OCT can be found. New scalar, strange mesons and Δ, N baryons with large effective masses can be located near them. The formation of Heron’s resonant triangles must be somehow related to the gravitational constant of free fall.
All rights reserved. Certificate No. 53172 dated 31.12.2024. Republic of Kazakhstan.
Introduction
The ends of the velocity vectors of the decay resonance particles are represented by material points of the velocity space located inside a sphere of radius C (C is the speed of light, the points are assigned the rest masses of the decay particles) [2, 9].
The Lorentz group defines in the velocity space the Lobachevsky geometry of curvature k = -1/ C2 [1–2]. Material points inside a sphere of radius C represent the Beltrami model of hyperbolic Lobachevsky velocity space (HLVS) [2,7].
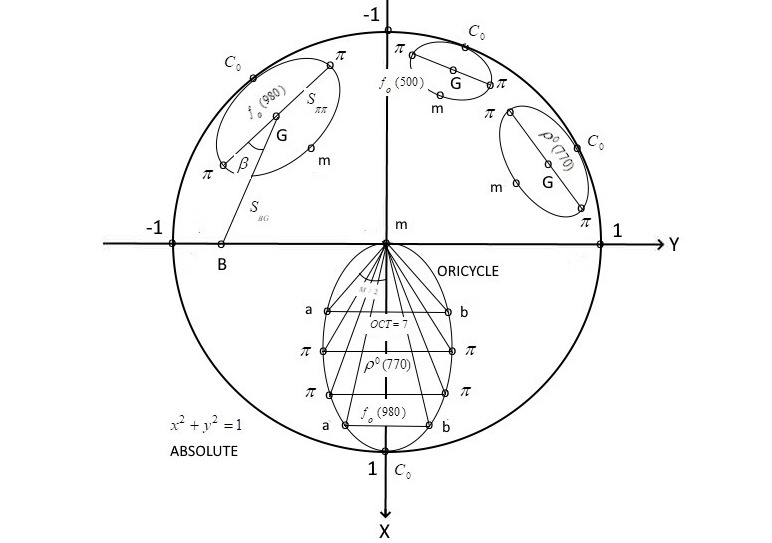
at the point “C0“ of the Absolute.
In the Beltrami model the straight lines and planes represent the straight lines and planes of HLVS [7]. The sphere of radius C, called the Absolute, represents infinitely distant points of HLVS.
A pair of material points of 2-part resonance decay in HLVS can be connected by a straight line segment and an arc of zero curvature line, called the oricycle [7,10]. All oricycles are congruent, just as straight lines in Euclidean space are congruent. In Fig_1, in the plane “π”, “π”, “B” (“B” is the velocity of the beam particle B), individual ellipses of oricycles of scalar mesons, whose centers “C0” lie on the Absolute, combined into one oricycle with a common center “C0”.
Archimedes’ laws of levers define a 3rd velocity point “m” on the oricycle arc, in which the role of the lever forces is played by the rest masses of the decay particles, and the lever arms are equal to the oricycle arcs. Thus, to the two material points “π”, “π” with rest masses mπ, a 3-rd velocity point “m” with an additive mass (mπ + mπ) is added. Connecting 3 points with straight line segments, we obtain an isosceles triangle Δπmπ of the resonance decay inscribed in the oricycle (Fig_1). In the triangle Δπmπ the golden ratio is discovered and the Stewart and Bretschneider theorems are fulfilled on the arcs of the oricycle (see Appendix). The length of the base of the triangle Δπmπ of the resonance decay is determined by its effective mass (2) [4–5].
Near the decay triangles of scalar, strange mesons and Δ, N baryons, satellite triangles with integer values of characteristics were discovered. Namely, for the satellite triangles, the function – the product of the length of the arc of the oricycle subtending their bases, multiplied by the cotangent of half the angle at the vertex opposite the base, takes on integer values. The function is called the oricyclic cotangent of a triangle (OCT) (see Tables 1–4). From Tables 1–4 it is clear that in addition to integer values of OCT, the sum of the hyperbolic cosines of the side lengths and the hyperbolic cosines of the base lengths of the satellite triangles are integers. Therefore, the satellite triangles are called Heron’s resonant triangles.
The discovery of Heron’s resonant triangles leads to the discovery of a regular structure in the directions of resonance decays. Usually, the decay of a resonance is studied in its rest frame through the angle between the direction of the momentum of the decay particle and a given quantization axis. In our case, it seems natural to study the decay of a resonance in the reference frame “m” of the additive mass of the decay particles and to choose the quantization axis along the tangent to the point “m”. Tables 1–4 show the values of the cosines of the angles between the tangent at point “m” of the additive mass and the tangent at the velocity point of the base of the Heron’s resonant triangle (cosine values > 1 mean that the hyperbolic cosines of the lengths of the segments corresponding to the angles at the intersection point of the tangents outside the Absolute are calculated) (Fig_7). From Tables 1–4 it is evident that Heron’s resonant triangles near scalar, strange mesons and Δ, N baryons have multiples of ½ of the cosine values of the angles.
Thus, Heron’s resonant triangles near the triangles of the listed resonances determine the rigid structure of integers on the entire infinite straight line (m – C0) (Fig_3). When moving along it, new Heron’s resonant triangles with large OCT can be found, near which new resonances with large effective masses can be found.
The decay of resonances along the oricycle occurs with acceleration under the combined action of the relative motion of the decay particles and the gravitational forces of the rest masses. Therefore, the formation of Heron’s resonant triangles must be somehow related to the constant of acceleration of gravity.
Decays of scalar, strange mesons and Δ, N baryons in the Beltrami model of Lobachevsky velocity space

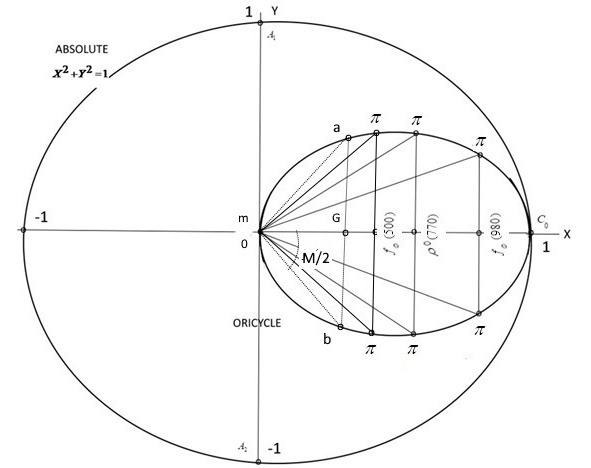
On the triangle Δamb the function oricyclic cotangent of a triangle (OCT) is introduced:
OCT = 𝑙ab * ctg (M/2), 𝑙ab = 2 * sh(Sab/2) (1)
where 𝑙ab is the length of the oricycle arc subtending the base of length Sab, M is the angle at the vertex “m”. The length Sab is called the rapidity [11]. When the base of the triangle Δamb is “near” the base of the Δπmπ decay of the scalar meson, the OCT function takes integer values. Table 1 shows the values OCT of those Δamb whose bases are at a “distance” 𝑙bπ / 𝑙ππ from the bases of the Δπmπ scalar mesons ( 𝑙bπ, 𝑙ππ are the lengths of the arcs of the oricycle between the points “b”, “π” and “π”, “π”). As can be seen from Table 1, for triangles Δamb, in addition to the integer OCT, the sum chSma + chSmb of the hyperbolic cosines of the lengths of the lateral sides and the hyperbolic cosines of the lengths of the bases chSab are also equal to integers. These triangles Δamb are called Heron’s resonant triangles.
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.