Бесплатный фрагмент - ФИЗИЧЕСКАЯ ПРИРОДА АТМОСФЕРНЫХ ВИХРЕЙ

3

Белов Николай Николаевич, кандидат педагогических наук,

учитель физики Карачевской ООШ

Козловского района Чувашской Республики

ФИЗИЧЕСКАЯ ПРИРОДА АТМОСФЕРНЫХ ВИХРЕЙ

Вначале рассчитаем динамичесчкое давление жидкости или газа плотности ρ на боковую поверхность герметически закрытого цилиндрического сосуда высотой h с радиусом оснований r, вращающегося стационарно и равномерно с угловой скоростью ω вне поля тяготения как твердое тело вокруг оси симмерии (см. Рис.1)

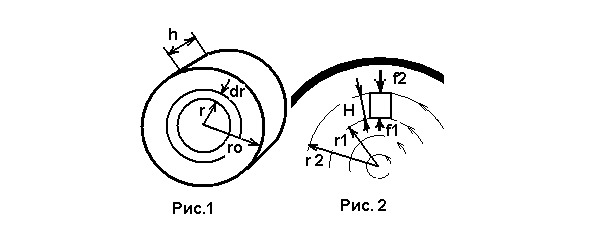
Для расчета давления разобьем цилиндр на совокупность полых цилиндров одинаковой высоты h толщиной стенок dr, во много раз меньший r, тогда можно считать, что все точки выделенного полого цилиндра находятся на расстоянии r от оси. В выделенном объеме dv = 2πrdrh заключена жидкость или газ массой dm = ρ2πhrdr. Этой массе жидкости сообщает центростремительное ускорение сила давления слоя, находящегося на расстоянии r + dr от оси. Согласно второму закону Ньютона df = dmdυ/dt, т.к. dυ/dt = ωr.

Динамическое давление, производимое выделенным слоем жидкости или газа на внешнюю боковую поверхность полого цилиндра dp = df/ds, где ds= 2πrh. — площадь боковой поверхности этого полого цилиндра.

С учетом всех указанных выше равенств находим элементарное давление:

dp=ρωrdr (1)

Суммарное давление, производимое всеми слоями вращающейся жидкости найдем, взяв определенный интеграл:

p = ρωrdr = 0,5ρ ωr. (2) Или, заменив в полученном выражении поизведение угловой скорости на радиус окружности через линейную скорость υ = ωr имеем:

р = 0,5ρυ. (3)

Выражения (2) и (3) выведены для случая, когда жидкость или газ целиком заполняют сосуд. Рассчитаем давление жидкости или газа толщиной потока. Рассмотрим два разных случая а) частицы вращаются с одинаковой угловой скоростью, тогда в выражении (2) следует изменить нижнюю границу интегрирования:

р = ρωr dr = ρω0,5 (r+ r) (r- r). (4)

Итак, в этом случае гидродинамическое давление прямо пропорционально плотности, квадрату угловой скорости, толщине потока (r- r) и радиусу кривизны среднего слоя — 0,5 (r+ r).

Если частицы потока имеют одинаковую скорость, например, совершая отражение, давят на лопасти турбины Пельтона при трогании с места, тогда в выражении (1) угловую скорость выразим

через линейную скорость и радиус кривизны ω = υ/r. При взятии интеграла (2) вынесем за знак интеграла плотность и линейную скорость. Давление в этом случае будет:

p = ρυ= ρυln. (5)

Из этого выражения видно, что гидродинамическое давление прямо пропорционально плотности, квадрату линейной скорости и натуральному логарифму отношения радиусов кривизны поверхностей слоев, между которыми заключен поток. Заметим, что математический запрет r не равен нулю имеет реальный физический смысл — изменение импульсов частиц потока не происходят моментально и точно по ломаным линиям, а по сопряженным.

Сила давления на неподвижную лопасть турбины:

F = s ρυln. (8)

,где s — площадь проекции рабочей части лопасти на пепендикулярную к начальной скорости частиц потока.

Если лопасть турбины наберет скорость υ относительно земли, то поток приближается к лопасти со скоростью υ — υ, то именно квадрату этой относительной скорости прямо пропорциональна сила давления

F = s ρ (υ- υ) ln. (9)

Мощность турбины равна изменению кинетической энергии потока за единицу времени:

N = F υ = s ρ υ (υ- υ) ln. (10)

ВВЕДЕНИЕ ПОНЯТИЯ ЦЕНТРОСТРЕМИТЕЛЬНО-ВЫТАЛКИВАЮЩАЯ — ГИДРО-АЭРОДИНАМИЧЕСКАЯ АРХИМЕДОВА СИЛА

На более удаленную и перпендикулярную к радиусу r грань небольшого тела, находящегося во вращающемся потоке (см. Рис. 2) действует большее динамическое давление f=0,5ρωr s- эта сила давления больше, чем на противоположную грань

f= 0,5 ρωr s, а на другие попарно-противоположные грани действуют одинаковые силы давления, попарно компенсирующие друг-друга, поэтому результирующая всех сил давлений направлена к оси вращения и является гидродинамической Архимедовой силой:

F = ρω (r +0,5H) Hs. (11)

выражение, стоящее в скобках –это радиус, проведенный к центру масс тела, а высота тела равна разности радиусов Н= r- r;

m =ρHs — масса вытесненной жидкости;

ω (r +0,5Н) — центростремительное ускорение частиц, окружающих тело.

Итак, Гидродинамическая Архимедова сила равна по модулю произведению массы вытесненной телом жидкости или газа на центростремительное ускорение окружающих его частиц среды. Ярким проявлением такой Архимедовой силы объясняется движение чаинок к области оси вращения — чем больше квадрат угловой скорости вращения, тем быстрее чаинки достигают центра дна чашки.

Принцип действия центрифуги и сепаратора объясняется тем, что если пренебречь действием силы тяжести на тело, то согласно второму закону Ньютона

F = ma= ρsH, где ρ- плотность тела и оно получает ускорение, а под действием центростремительно направленной гидродинамической Архимедовой силы:

F = ρ ω (r +0,5H) Hs.

Приравняв левые части равенств и сократив на объем тела sH получим:

a= ρ ω (r +0,5H) / ρ. (12)

Из этого выражения видно, что если плотность примеси меньше плотности жидкости, то ускорение тела больше ускорения частиц жидкости, равной ω (r +0,5H) и вытесняется к центру, что и поясняет принцип сепарации.

Если плотность примеси больше плотности жидкости, то его ускорение меньше ускорения частиц среды, следовательно он удаляется от оси вращения, накапливается на стенке центрифуги.

Если упомянутые плотности равны, то такая примесь не отделима сепаратором или центрифугой.

В ультрацентрифугах очень велик квадрат угловой скорости, поэтому даже однородная жидкость или газ может дифференцироваться на слои разной плотности и даже разной среднеквадратической скорости (следовательно и температуры) — из-за из «вытеснения» — преимущесвенного возникновения и смещения областей молекулярных флуктуаций к оси обращения под действием гидро — и аэродинамической Архимедовой силы.