
Бесплатный фрагмент - Элементы комбинаторики, теории вероятностей и математической статистики
1. Основные формулы комбинаторики
Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств — правило суммы и правило произведения [1,6].
1.1.Правило суммы
Если конечные множества не пересекаются, то число элементов X U {или} Y равно сумме числа элементов множества X и числа элементов множества Y.
То есть, если на первой полке стоит X книг, а на второй Y, то выбрать книгу из первой или второй полки, можно X+Y способами.
Примеры задач
№1
Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение: X=17, Y=13
По правилу суммы X U Y=17+13=30 тем.
Ответ: 30 способов.
№2
Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет из спортлото или автомотолотереи?
Решение: всего 6+10=16 вариантов.
Ответ: 16 способов.
1.2.Правило произведения
Если элемент X можно выбрать k способами, а элемент Y — m способами, то пару (X,Y) можно выбрать k*m способами.
То есть, если на первой полке стоит 5 книг, а на второй 10, то выбрать одну книгу с первой полки и одну со второй можно 5*10=50 способами.
Примеры задач
№1
Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?
Решение: Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3=36 вариантов переплета.
№2
Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя — как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z -любые цифры, а X — не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9*10*10=900 вариантов.
Очень часто для наглядного решения таких задач применяются круги Эйлера.
Пример 1. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским и немецким одновременно владеют 8 человек, английским и французским — 10, немецким и французским — 5, всеми тремя языками — 3. Сколько туристов не владеют ни одним языком?
Решение: Выразим условие этой задачи графически (см. рис.1). Обозначим кругом тех, кто знает английский, другим кругом — тех, кто знает французский, и третьим кругом — тех, кто знают немецкий.
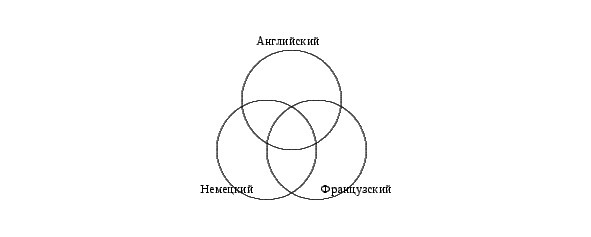
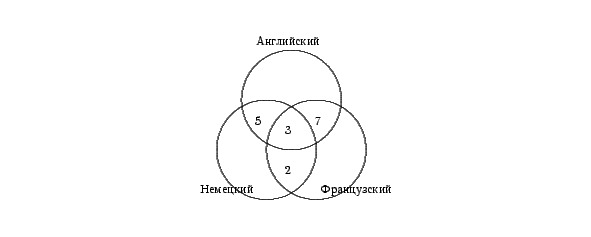
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языком владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10—3 = 7 человек.
Аналогично получаем, что только английским и немецким владеют 8—3 = 5 человек, а немецким и французским 5—3 = 2 туриста. Вносим эти данные в соответствующие части рисунка 2.
Определим теперь, сколько человек владеют только одним, из перечисленных языков. Немецкий знают 30 человек, но 5 +3 +2 = 10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским — 30 человек (см. рис.3).
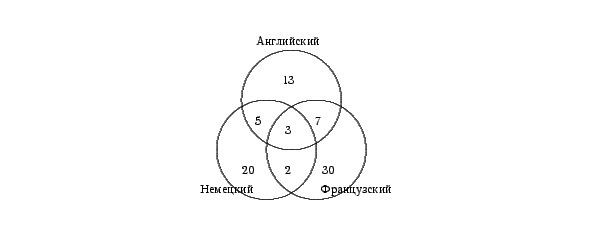
По условию задачи всего 100 туристов. 20+13+30+5+7+2+3=80 туристов знают хотя бы один язык, следовательно, 20 человек не владеют ни одним из данных языков.
Ответ: 20 человек не владеют ни одним из данных языков.
1.3. Размещения без повторений
Пример1. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны?
Это пример задачи на размещение без повторений. Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке считаются разными.
Если X-множество, состоящие из n элементов, m≤n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество А, содержащее m элементов из n элементов.
Количество всех размещений из n элементов по m обозначают (см. рис.4):
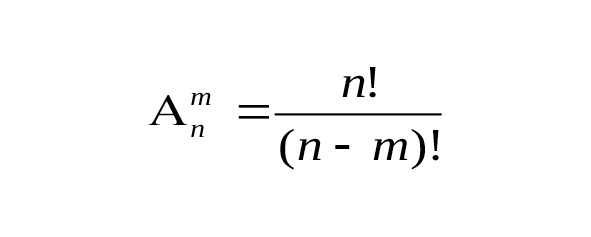
Где n! — n-факториал (factorial анг. сомножитель) произведение чисел натурального ряда от 1 до какого либо числа n. n!=1*2*3*…*n. 0!=1.
Значит, ответ на выше поставленную задачу будет следующим (см. рис.5):
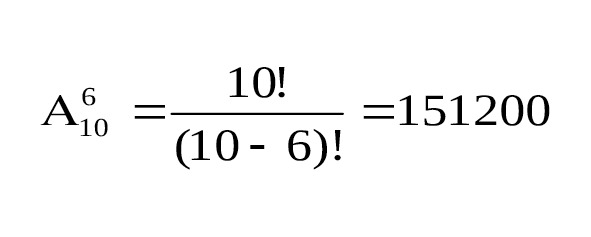
1.4. Перестановки без повторений
В случае n=m (см. размещения без повторений) А из n элементов по m называется перестановкой множества x.
Количество всех перестановок из n элементов обозначают Pn.
Pn=n!
Действительно при n=m (см. формулу на рисунке 6):
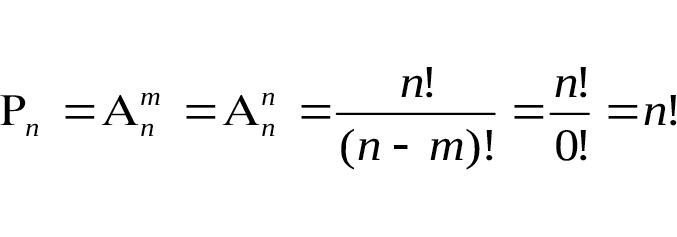
Пример 2. Сколько различных шестизначных чисел можно составить из цифр 0, 1, 2, 3, 4,5, если цифры в числе не повторяются?
Таким образом, количество вариантов при сочетании будет меньше числа вариантов размещений.
Число сочетаний из n элементов по m обозначается (см. рис.7).
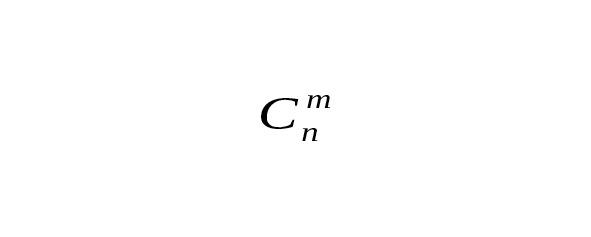
Решение:
Найдем количество всех перестановок из этих цифр: P6=6!=720.
Ответ: 720.
Пример 3.
«Проказница Мартышка, Осел, Козел, Да косолапый Мишка
Затеяли играть квартет…
Стой, братцы стой! — Кричит Мартышка, — погодите!
Как музыке идти? Ведь вы не так сидите…
И так, и э так пересаживались — опять музыка на лад не идет.
Тут пуще прежнего пошли у них раздоры.
И споры, Кому и как сидеть…»
Вероятно, крыловские музыканты так и не перепробовали всех возможных мест. Однако способов не так уж и много. Сколько?
Решение
Здесь речь идет о перестановке из четырех элементов,
Значит, возможно, P4=4!=24 варианта перестановок.
Ответ: 24.
1.5. Сочетания без повторений
Сочетанием без повторений называется такое размещение, при котором порядок следования элементов не имеет значения [2]
Всякое множество X состоящее из m элементов, называется сочетанием из n элементов по m.
Таким образом, количество вариантов при сочетании будет меньше числа вариантов размещений.
Число сочетаний из n элементов по m обозначается (см.рис.7).
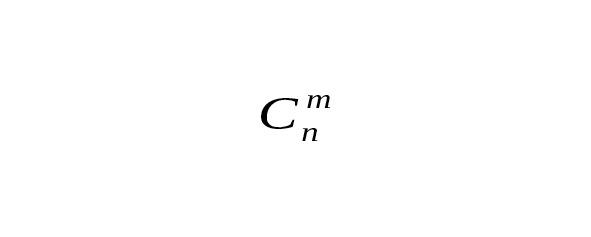
Формула для числа сочетаний из n элементов по m показана рис.8.
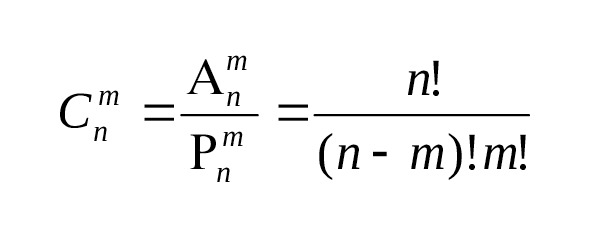
Пример 1. У одного человека 7 книг по математике, а у второго — 9. Сколькими способами они могут обменять друг у друга две книги на две книги.
Решение:
Так как порядок следования книг не имеет значения, то выбор 2 книг — сочетание.
Первый человек может выбрать 2 книги способами (как это показано на рис.9).
Второй человек может выбрать 2 книги способами (как это показано на рис.10).
Значит всего по правилу произведения возможно 21*36=756 вариантов.
Ответ: 756 вариантов.
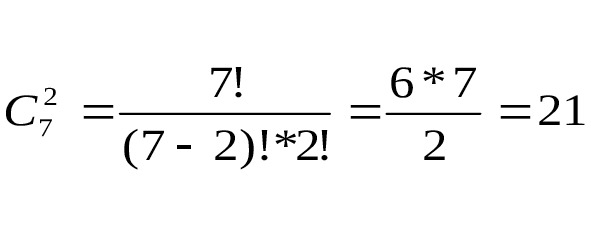
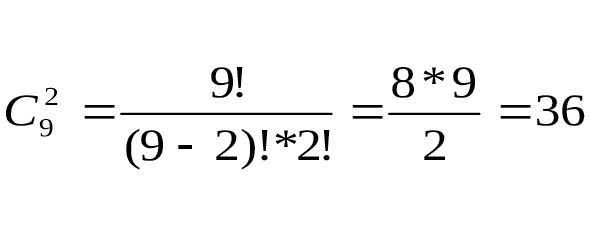
2. Решение типовых задач
Задача 1. Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение: X=17, Y=13
По правилу суммы X U Y=17+13=30 тем.
Ответ: 30 способов.
Задача 2. Имеется 5 билетов денежно-вещевой лотереи, 6 билетов спортлото и 10 билетов автомотолотереи. Сколькими способами можно выбрать один билет из спортлото или автомотолотереи?
Решение: всего 6+10=16 вариантов.
Ответ: 16 способов.
Задача 3. Переплетчик должен переплести 12 различных книг в красный, зеленый и коричневые переплеты. Сколькими способами он может это сделать?
Решение: Имеется 12 книг и 3 цвета, значит по правилу произведения возможно 12*3=36 вариантов переплета.
Ответ: 36 способов.
Задача 4. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя — как и вторая. Третья цифра будет любой. Это можно представить в виде XYZYX, где Y и Z -любые цифры, а X — не ноль. Значит по правилу произведения количество цифр одинаково читающихся как слева направо, так и справа налево равно 9*10*10=900 вариантов.
Ответ: существует 900 таких чисел.
Задача 5. Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец?
Решение: Два юноши не могут одновременно пригласить одну и ту же девушку. И варианты, при которых одни и те же девушки танцуют с разными юношами, считаются разными, поэтому, подсчет числа способов выглядит, как показано на рис.11:
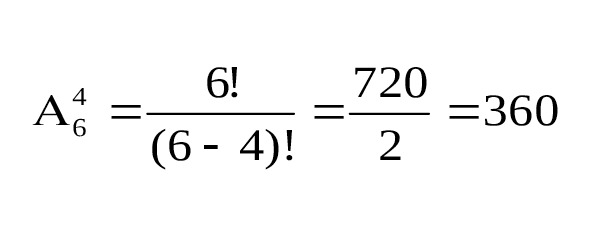
Ответ: Возможно 360 вариантов.
Задача 6. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр.
Решение:
Так как кнопки нажимаются одновременно, то выбор этих трех кнопок — сочетание. Отсюда, расчет числа возможных вариантов показан на рис.12.
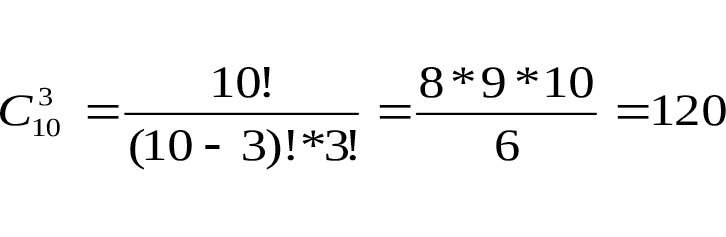
Задача 7. У одного человека 7 книг по математике, а у второго — 9. Сколькими способами они могут обменять друг у друга две книги на две книги.
Решение:
Так как порядок следования книг не имеет значения, то выбор 2 книг — сочетание. Первый человек может выбрать 2 книги способами. Второй человек может выбрать 2 книги. Значит всего по правилу произведения возможно 21*36=756 вариантов. Расчеты приведены на рис.13 и 14.
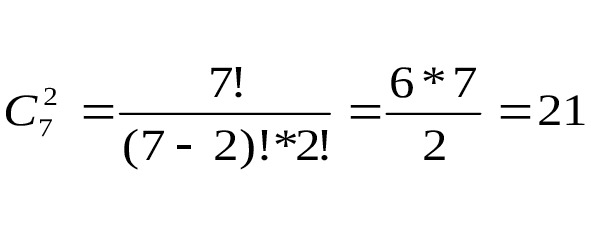
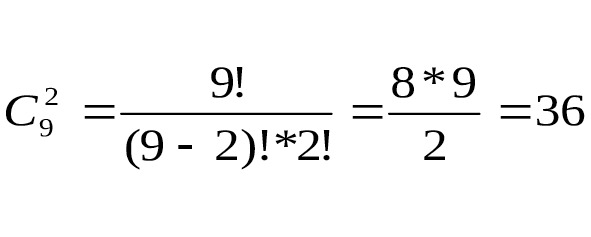
Задача 8. При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать?
Решение:
Первый игрок делает выбор из 28 костей. Второй из 28—7=21 кости, третий — из14, а четвертый игрок забирает оставшиеся кости.
Следовательно, общее число способов можно подсчитать по формуле на рисунке 15.
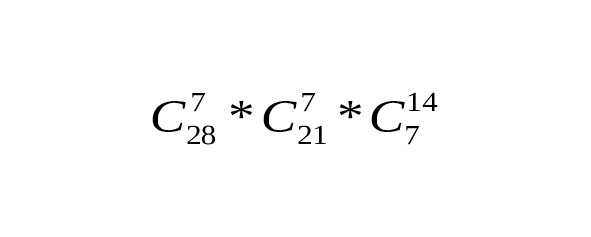
САМОСТОЯТЕЛЬНО
Задача 1. У мамы 2 яблока и 3 груши. Каждый день подряд она выдает по одному фрукту.
Сколькими способами это может быть сделано?
Ответ: 10ю способами.
Задача 2.Предприятие может предоставить работу по одной специальности 4 женщинам, по другой — 6 мужчинам, по третьей — 3 работникам независимо от пола. Сколькими способами можно заполнить вакантные места, если имеются 14 претендентов (6 женщин и 8 мужчин)?
Ответ: 1680ю способами
3.Основные понятия теории вероятностей
Теория вероятностей — раздел высшей математики, изучающий закономерности массовых случайных явлений [3,4].
Совершенно очевидно, что в природе нет ни одного физического явления, в котором не присутствовали бы в той или иной мере элементы случайности.
Как бы точно и подробно ни были фиксированы условия опыта, невозможно достигнуть того, чтобы при повторении опыта результаты полностью и в точности совпадали. Случайные отклонения неизбежно сопутствуют любому закономерному явлению. Тем не менее, в ряде практических задач этими случайными элементами можно пренебречь, рассматривая вместо реального явления его упрощенную схему, «модель», и предполагая, что в данных условиях опыта явление протекает вполне определенным образом. При этом, из бесчисленного множества факторов, влияющих на данное явление, выделяются самые главные, решающие; влиянием остальных, второстепенных факторов просто пренебрегают. При использовании этой схемы для решения любой задачи, прежде всего, выделяется основной круг учитываемых условий и выясняется, на какие параметры задачи они влияют; затем применяется тот или иной математический аппарат; таким образом, выявляется основная закономерность, свойственная данному явлению, и дающая возможность предсказать результат опыта по его заданным условиям.
Однако для решения ряда вопросов описанная схема — классическая схема так называемых «точных наук» — оказывается плохо приспособленной.
Существуют такие задачи, где интересующий нас исход опыта зависит от столь большого числа факторов, что практически невозможно зарегистрировать и учесть все эти факторы. Это задачи, в которых многочисленные второстепенные, тесно переплетающиеся между собой случайные факторы играют заметную роль, а вместе с тем число их так велико и влияние столь сложно, что применение классических методов исследования себя не оправдывает.
Все подобные задачи требуют изучения не только основных, главных закономерностей, определяющих явление в общих чертах, но и анализа случайных возмущений и искажений, связанных с наличием второстепенных факторов и придающих исходу опыта при заданных условиях элемент неопределенности.
Очевидно, что должна существовать принципиальная разница в методах учета основных, решающих факторов, определяющих в главных чертах течение явления, и вторичных,
второстепенных факторов, влияющих на течение явления в качестве «погрешностей» или «возмущений». Элемент неопределенности, сложности, многопричинности, присущий случайным явлениям, требует создания специальных методов для изучения этих явлений.
Такие методы и разрабатываются в теории вероятностей. Ее предметом являются специфические закономерности, наблюдаемые в случайных явлениях.
Практика показывает, что, наблюдая в совокупности массы однородных случайных явлений, мы обычно обнаруживаем в них вполне определенные закономерности, своего рода устойчивости, свойственные именно массовым случайным явлениям.
Например, если много раз подряд бросать монету, частота появления герба (отношение числа появившихся гербов к общему числу бросаний) постепенно стабилизируется, приближаясь к вполне определенному числу, а именно к 1/2.
Отметим, что именно массовость случайных явлений обеспечивает выполнение этой закономерности.
Подобного рода закономерности (их называют «статистическими») возникают, когда мы наблюдаем в совокупности массивы однородных случайных явлений. Они оказываются практически независимыми от индивидуальных особенностей отдельных случайных явлений, входящих в массив: эти особенности как бы взаимно погашаются, нивелируются; выражаясь образно, «из множества беспорядков возникает порядок». Средний массовый результат множества случайных явлений оказывается практически уже не случайным, предсказуемым. Это и является базой для практического применения вероятностных (статистических) методов исследования.
Методы теории вероятностей не отменяют и не упраздняют случайности, непредсказуемости исхода отдельного опыта, но дают возможность предсказать, с каким-то приближением, средний суммарный результат массы однородных случайных явлений.
Цель вероятностных (статистических) методов — в том, чтобы, минуя слишком сложное (и зачастую практически невозможное) исследование отдельного случайного явления, обратиться непосредственно к законам, управляющим массами таких явлений. Изучение этих законов позволяет не только осуществлять прогноз в области случайных явлений, но и целенаправленно влиять на ход этих явлений, контролировать их, ограничивать сферу действия случайности, сужать ее влияние на практику.
В настоящее время нет практически ни одной области науки, в которой в той или иной степени не применялись бы вероятностные методы. В одних науках, в силу специфики предмета и исторических условий, эти методы находят применение раньше, в других — позднее.
Исторически первые зачатки вероятностных методов с довольно примитивным математическим аппаратом возникли в XVII в. при разработке теории азартных игр с целью дать рекомендации игрокам. Затем эти методы стали применяться в практике страховых компаний для установления разумных размеров страховых премий.
Постепенно область применения вероятностных методов расширялась. Сегодня биология, физиология, медицина, социология все шире применяют вероятностные методы. Не чуждаются их и такие «исконно гуманитарные» науки, как психология, лингвистика, литературоведение, даже эстетика.
Рассмотрим некоторый опыт. Каждый исход опыта обозначим элементарным событием, где n — число исходов данного опыта.
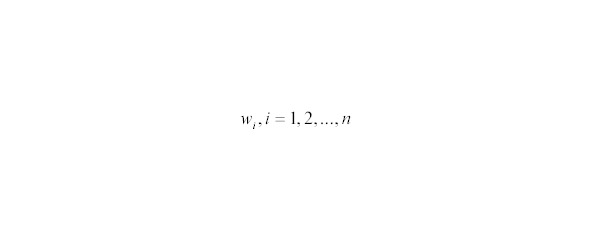
Множество всех возможных исходов опыта образуют — универсальное множество опыта или пространство элементарных событий (см. рис.16 и 17).
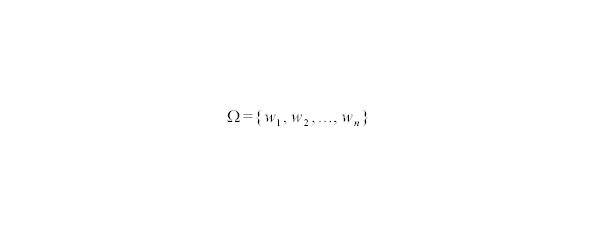
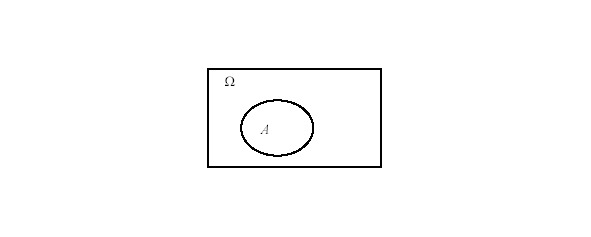
Тогда любое случайное событие А, возможное в данном опыте, есть некоторое подмножество универсального множества
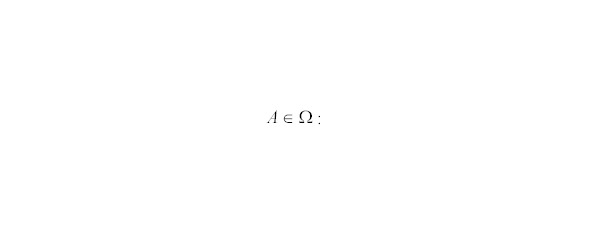
,
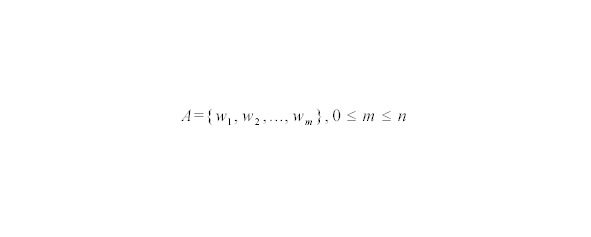
Событие А называется достоверным, если, т.е. происходит в каждом опыте.
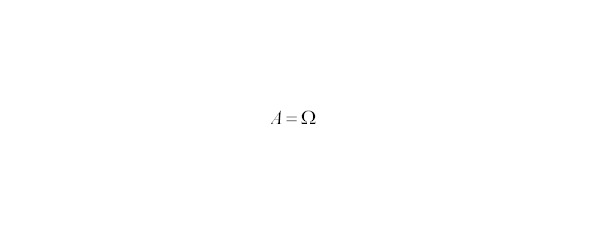
Событие А называется невозможным, если, т.е. никогда не происходит в данном опыте.
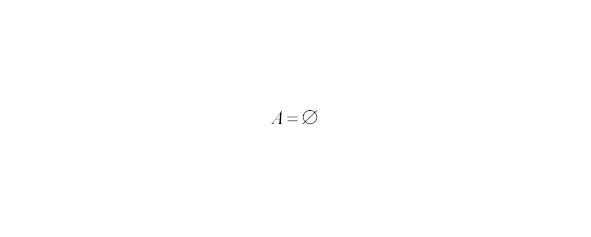
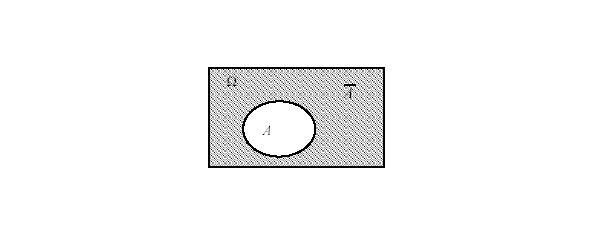
Противоположным к событию А называют событие, состоящее в невыполнении А, т.е. оно происходит всегда (см. рис.18), когда не происходит A.

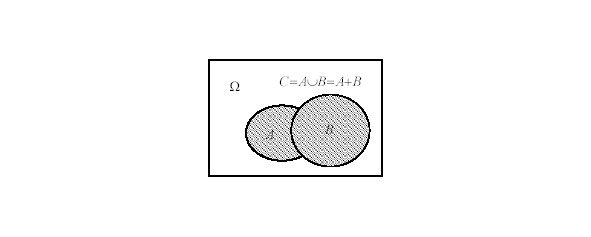
Событие С называется суммой событий А и В, если оно происходит тогда, когда происходит либо А, либо В, либо оба одновременно (хотя бы одно событие), смотрите рис.19 и 20.
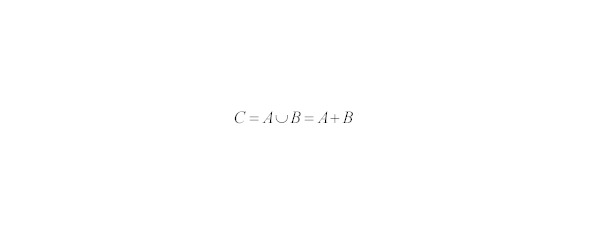
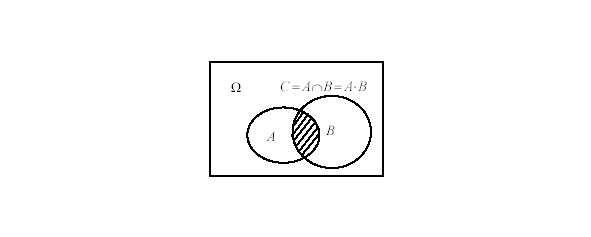
Событие С называется произведением событий А и В,, если С происходит тогда, когда происходят и А и В одновременно (см. рис.21 и 22).
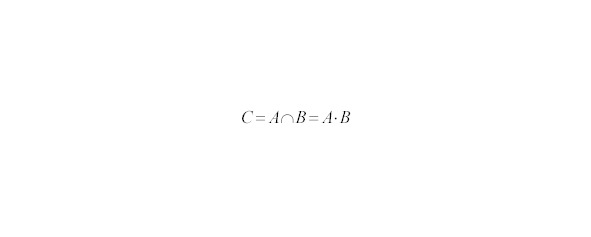
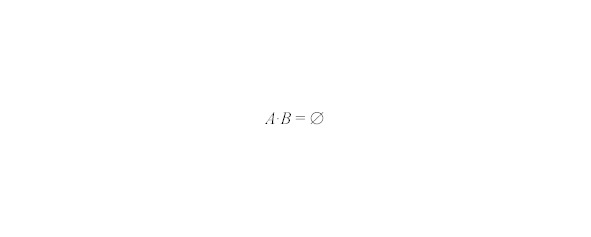
События А и В несовместны, если они не могут произойти одновременно, т.е..
События Ai (i = 1, 2, …, n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие (рис.23).
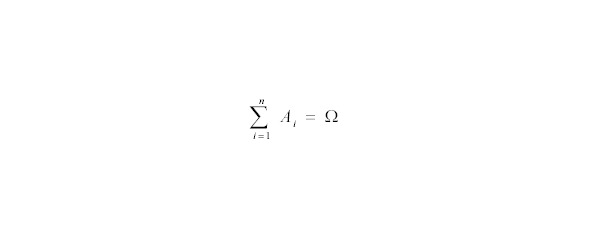
При преобразовании выражений можно пользоваться следующими тождествами (см. рис.24):
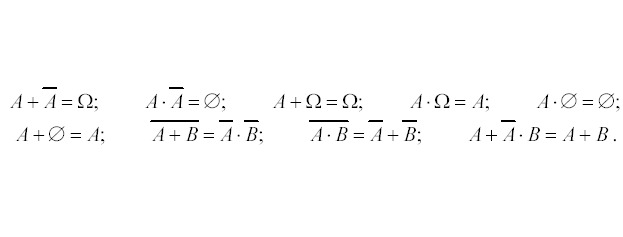
Аксиома 1. Вероятность p (А) случайного события А есть функция множества элементарных исходов, благоприятных событию А, и вероятность любого события принимает значения:
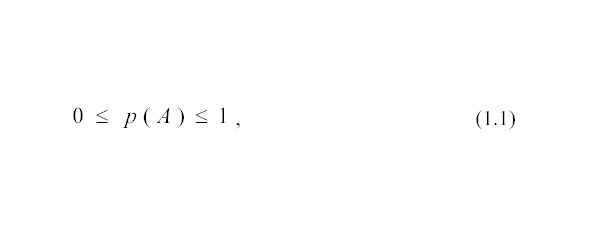
при чем (рис.25):
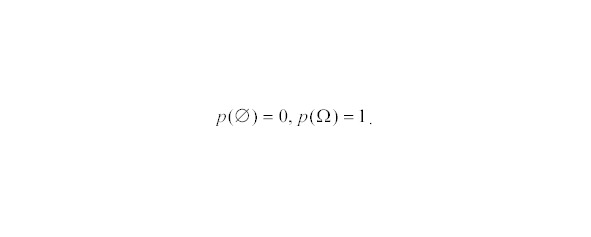
Аксиома 2. Вероятность суммы несовместных случайных событий равна сумме вероятностей этих событий:
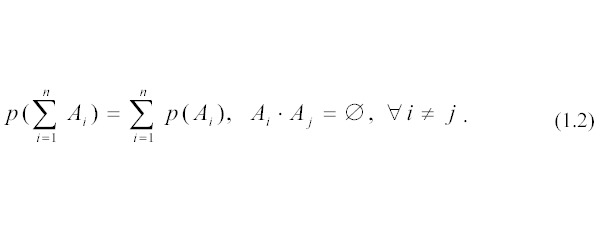
Следствие аксиом 1 и 2 (рис.26):
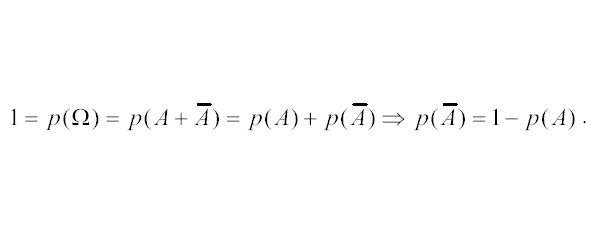
3.1.Классическая формула вероятности
События А1+ … +Аn называются случаями, если они обладают следующими свойствами (см. рис.27):

Пусть некоторый опыт сводится к схеме случаев, тогда вероятность события А в этом опыте равна отношению числа благоприятных случаев к общему числу случаев (см. рис.28):
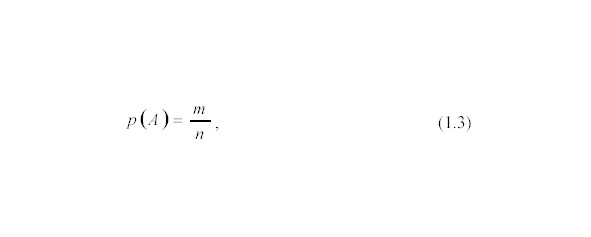
где m — число случаев Аi, благоприятных событию А, т.е. входящих в множество А = {А1 +Аm};
n — число всех возможных случаев.
Доказательство.
Очевидно, что A = A1 + A2 + + + Am. Так как Аi несовместимы, то определим вероятность события A по второй аксиоме:
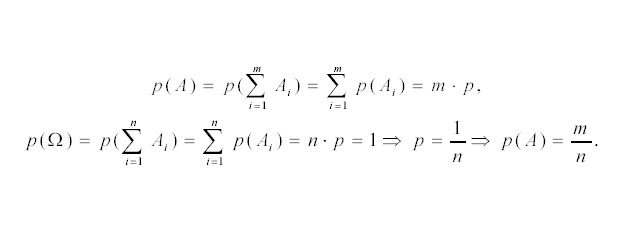
Бесплатный фрагмент закончился.
Купите книгу, чтобы продолжить чтение.
