Бесплатный фрагмент - Data Science для новичков

От автора

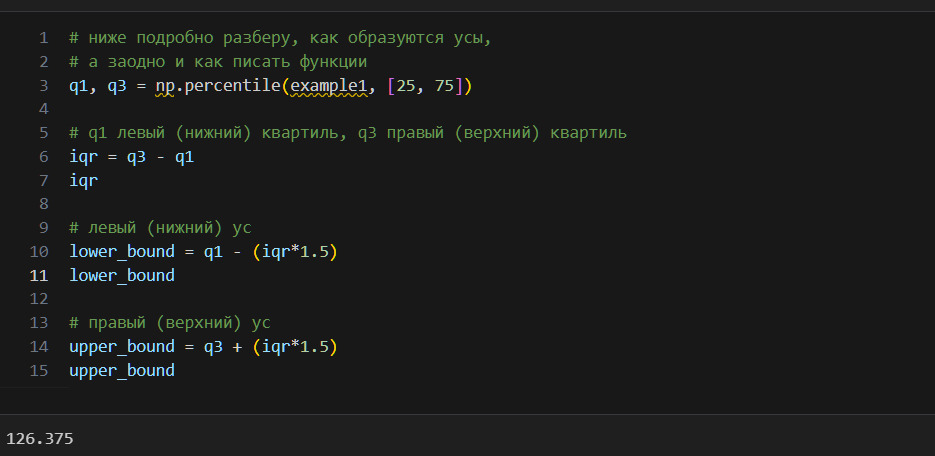
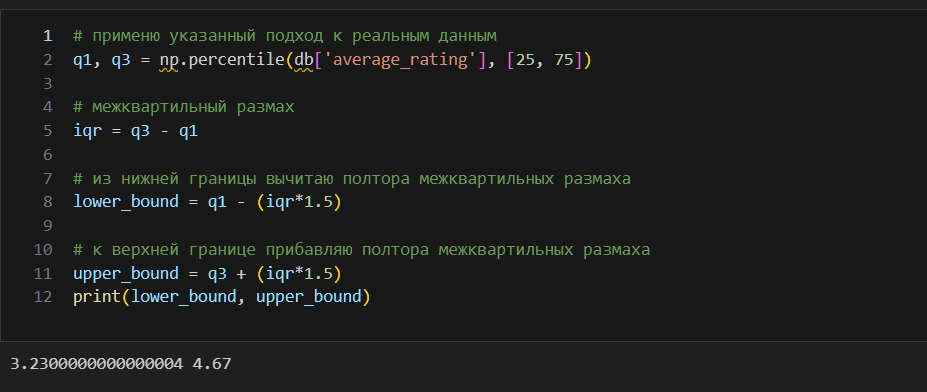
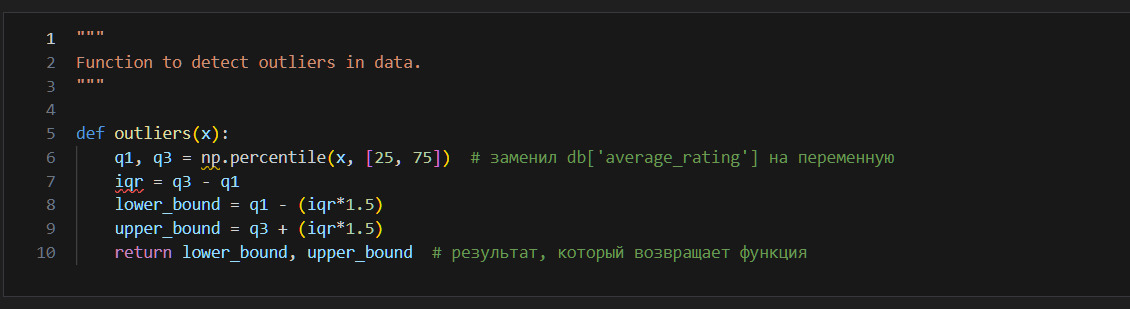
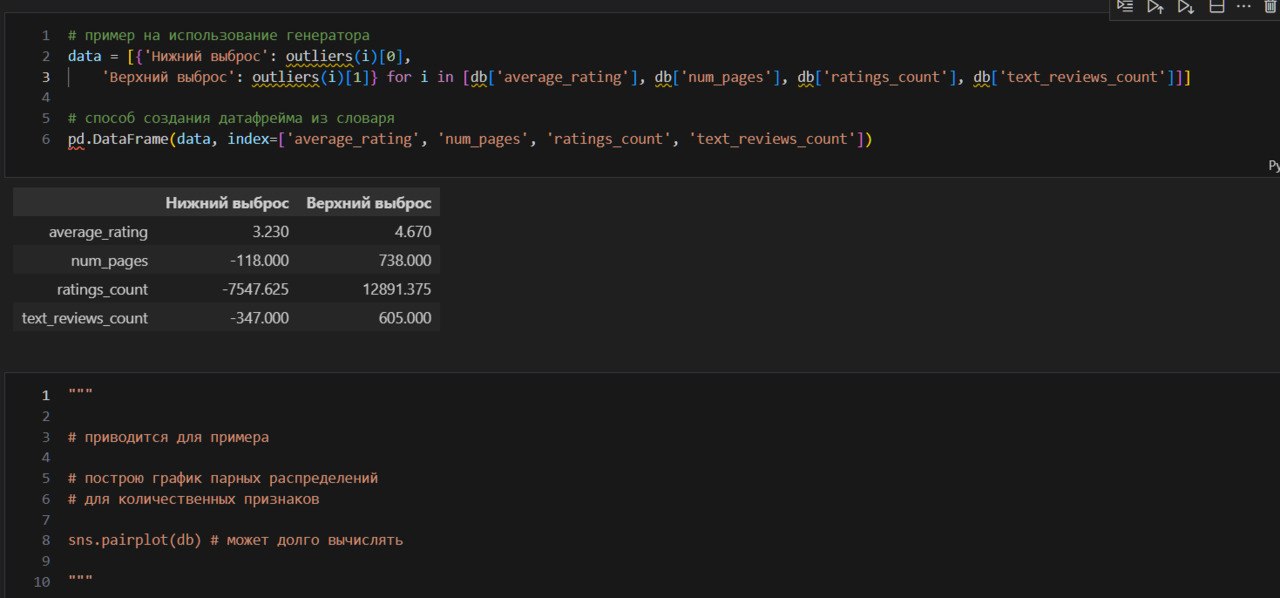
В этой книге я собрал все 1) важные и 2) базовые знания по Data Science.

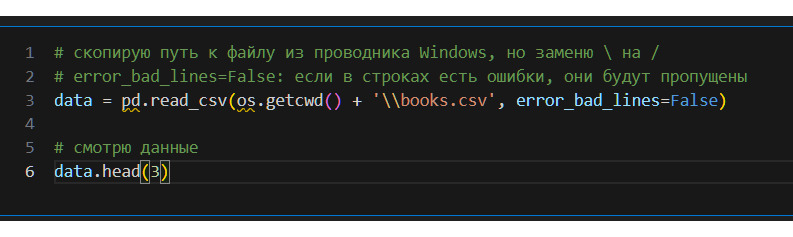
В книге код дан так, как вы его увидите в Visual Studio Code.

По тексту много ссылок на другие книги, учебники, пособия в онлайне. Рекомендуется ознакомиться с этими материалами. Моя книга может служить только своеобразным путеводителем на начальном уровне для всех, кто желает стать специалистом по Data Science.

Принципы образования

Здесь я собрал несколько практических советов, принципов самообразования.

1. Прежде, чем начинать изучение новой науки, надо понять зачем вы это делаете. Карьера, деньги? Да, многие учатся ради этого. Но это слишком незначительно для человека. Деньги и карьера могут быть побочным продуктом от учебы, но не должны быть основными причинами. Ставьте себе великие цели. Если беретесь за математику, то ваша цель — решить одну из задач Гилберта. Если беретесь за DS, то ваша задача — изобрести искусственный интеллект. Не меньше этого. Пускай даже в итоге это у вас не получится, но идти надо по пути великих целей. Только так вы сможете убедить себя, что огромные усилия, которые вы будете прикладывать, стоят того. Только так вы сможет сделать учебу интересной для себя.

2. Ваш план образования должен иметь два направления: сложное и простое. Например, сложное — математика, простое — публицистические книги про ИИ, основы программирования. Почему? Чтобы мозг не скучал. И чтобы мозг понимал, что вы занимаетесь сложной задачей и поэтому мозг должен работать максимально эффективно. Кроме того, пока мозг не ощущает опасность, он не начинает работать на максимальном уровне. Теория вероятностей вполне может быть такой опасностью. Делить учебу на сложные и простые занятия важно еще и потому, что так можно эффективно расходовать время. Если вы слишком заняты другими делами, вы болеете или устали, то можно взять легкие дела из плана учебы. Когда вы освободитесь, то можно будет заняться максимально сложными делами. Вы все время учитесь, а это очень важно. Помните, что нельзя тратить время.

3. Не пытайтесь все понять и запомнить с первого раза. Не надо себя насиловать. Пока вы учите новую науку, ваша задача не запомнить, а понять. Если вы поняли дифференциальное исчисление, а затем забыли половину теорем дифференциального исчисления, то ничего страшного. Понимание прежде всего!

4. Учитесь «слоями». Прочитайте книгу, например, по математике. Попытайтесь понять максимально много, но без насилия над собой. Не пытайтесь запомнить все теоремы, формулы. Ваша задача — понять, повторюсь. Теперь возьмите следующую книгу по математике. Попытайтесь понять максимально много. В этот раз вы поймете уже гораздо больше. Продолжайте, не останавливайтесь. Запомните, нельзя полностью выучить математику, Data Science или любую науку. Ваша цель — тренировать способность понимать. Чем больше будет «слоев» понимания, тем лучше.

5. Новый «слой» должен быть чуть сложнее предыдущего. Например, начните с учебника по математике для школы, затем возьмите учебник для университетов. Не останавливайтесь на этом «слое». Возьмите специальные книги, например подробное изложение линейной регрессии.

6. Не перечитывайте книги, которые вы уже прочитали. Если вы не понимаете какую-то тему, то лучше взять другую книгу по этой теме (или почитать пост в каком-то блоге). Однако у вас должна быть «опорная книга», например по математике, DS, программированию. Это такая книга, которая, на ваш взгляд и для вас, содержит самое простое и полное изложение темы. Это будет ваш справочник. Перечитывать такие книги можно.

7. Не бойтесь сложных книг. Даже если из всей книги вы поняли только 90%, польза огромная. Вы учите свой мозг чувствовать себя как дома в той теме, которой посвящена книга. Вы учите мозг не бояться этой темы. Вы учите термины, теоремы, формулы, алгоритмы.

8. Никогда себя не ругайте. Если что-то не получается сейчас, то это получится потом. Главное — это идти по правильному пути. Это не означает, что вы не должны заниматься самоанализом. Почему что-то не понятно? Что можно сделать, прочитать, чтобы лучше это понять?

9. Создавайте теории. Всегда создавайте теории, идеи. Не ждите, когда станете профессионалом. Ищите необычные решения, делайте безумные предположения, даже если только начали читать первые книги по математике. Главное помнить, что любая идея должна быть проверена. Пусть такой проверкой будет следующая книга или ваш личный проект.

10. Не соглашайтесь с идеями типа «математика это сложно». Не позволяйте себя этим пугать. Для человека нет ничего сложного. Что такое «сложно»? Любое знание — это объекты и связи между ними. «Сложно» — это значит много объектов, много связей. Базовый принцип для приготовления бутерброда и решения математических задач один: возьмите элементы и свяжите их. Нет никакой абстрактной «сложности». Если все дело в количестве элементов и связей, то вам просто нужно время. Базовый принцип вы уже знаете и даже блестяще им владеете (бутерброды же хорошо у вас получаются!).

11. Если вы не понимаете книгу по математике или DS, то причина просто в том, что у вас нет навыка и вы не знаете всех предпосылок. Почему, например, книги по экономике не кажутся такими сложными? Потому что многие понятия из экономики знакомы нам: безработица, прибыль и т. п. Но элементы математики, особенно абстрактной, мы встречаем в жизни редко. Возьмем теорему математики. В том учебнике, который вы читаете, нельзя рассказать все причины, по которым возникла эта теорема. Поэтому вы можете не понять эту теорему. Это не ваша вина. Вы поймете эту теорему, пускай и в следующем «слое». И еще, помните, что формулы на самом деле очень упрощают жизнь! Не обращайте внимание на слова «это очевидно» и т. п. Возможно, это очевидно автору, но не вам. В этом нет проблемы!

12. Создавайте контекст. Что такое контекст? Вы читаете учебники по математике. Но вы должны также читать книги по истории математики, по философии математики и т. п. Чем больше разных знаний у вас будет, тем лучше. Так нашему мозгу легче запоминать и так мозг лучше понимает. Помните, наш мозг воспринимает информацию из контекста, потому что мир тоже состоит из связей.

13. Делайте упражнения. Но только, когда нет других более важных дел. Упражнения, как правило, это искусственные примеры, которые являются скучными и мало применяются в жизни. Например, в обучении языку давно уже поняли, что искусственные примеры — это плохой способ учить язык. Кроме того, упражнения из учебника часто пытаются вас запутать. Это плохо. Зачем? Вам должны объяснять. Опыт придет на конкретных примерах из жизни. Поэтому создавайте свои проекты. Пускай это будут примеры, которые основаны на понятных для вас проблемах. Может быть, вам интересно применить методы математики и DS для изучения экологических проблем. Займитесь этим!

14. Ищите хорошие книги. Как это сделать? Возьмите пять книг по одной теме наугад. В этих книгах будут ссылки на другие учебники, книги. Дальше собирайте библиотеку и читайте эти книги. И добавьте в эту библиотеку классические книги по теме. Это всегда хорошее решение!

15. Не смешивайте занятия. Если сейчас вы учите математику, то не пытайтесь вспомнить код из последнего проекта.

16. Старайтесь объяснять все своими словами. Вы учитесь, накапливаете знания. Расскажите о своих знаниях! Это может быть блог или подкаст. Если можете своими словами объяснить, значит хорошо все поняли.

17. Не бойтесь, что вы медленно учитесь. Главное учиться.

18. Найдите хобби. Пускай ваше хобби будет способом отвлечься от учебы. Это тоже необходимо. Умейте отдыхать! Возьмите пару недель или месяц, чтобы отдохнуть. Пока вы отдыхаете, мозг приводит ваши знания в порядок и находит неожиданные связи.

Глава 1. Подготовка данных

Data Science содержит три больших отдела:

1) получение и подготовка данных;

2) статистическая обработка данных;

3) машинное обучение.

Статистическая обработка нацелена на:

1) описание сгруппированных данных (медиана, среднее и т.п.);

2) описание взаимодействия между различными группами данных (корреляция и т.п.).

Другими словами, статистическая обработка требует понять данные, а значит и те реальные процессы, которые стоят за данными. Это важно учитывать. В конечном счете моя задача не просто получить корреляцию, а понять данные. Что это означает? Во-первых, я должен проверять как корреляцию, так и другие статистики, на вменяемость, на соответствие действительности. Во-вторых, именно в действительности я должен искать подсказки, какие тесты применить, какие метрики получить. Так, например, понимание данных можно получить и из других источников, не только за счет применения статистических тестов. Можно сделать предположения о процессах, отраженных в данных, на основании опыта, а уже затем проверить предположения с помощью статистики. Важно помнить, что математика — это только язык, который используют, чтобы описать действительность. Не надо подменять математикой саму действительность.

Машинное обучение нацелено на создание алгоритма, который позволит предсказывать целевой признак на основании заданных признаков в автоматизированном режиме. Другими словами, статистическая обработка позволяет понять процессы, а машинное обучение — предсказать процессы.

Однако начинается все с предварительной подготовки данных. В самом деле, если не подготовить данные, не убрать пропуски, дубликаты и т.п., то это повлияет на качество как статистической обработки, так и машинного обучения (или даже не позволит их выполнить). В этом разделе я займусь именно подготовкой данных.

Подготовка данных включает, но не ограничивается, следующие элементы:

1) проверка правильности формирования индекса, наименования столбцов (признаков). Например, может быть обнаружено, что в наименовании столбцов есть лишние пробелы;

2) проверка типа данных. Например, численные данные могут быть отмечены как объекты или наоборот;

3) поиск дубликатов;

4) очистка строковых данных от лишних символов. Например, наличие слэша там, где это очевидно неуместно;

5) обработка значений, которые очевидно являются ошибочными. Например, в столбце с количеством страниц указан жанр книги и т.п.;

6) создание новых признаков. Например, по значениям двух уже имеющихся столбцов можно создать третий;

7) укрупнение категорий в категориальных признаках;

Предупреждение об источнике данных

Источник данных находится по адресу https://www.kaggle.com/jealousleopard/goodreadsbooks. Мне неизвестна процедура, которую применял автор для сбора данных. Поэтому всегда надо помнить, что особенности именно данного набора могут оказать влияние на выводы. Идеально было бы самостоятельно собрать данные или использовать дополнительно иные сборки данных, но пока в этой методичке такая задача не стоит. Кроме того, сайт Goodreads с конца 2020 ограничил использование API и получение данных.

Почему при таких ограничениях я выбрал именно данный набор? Как я указывал выше, прежде всего, надо основываться на действительности, чтобы понять данные. А значит я должен разбираться или хотя бы понимать те объекты, тот предмет, которого касаются данные. Так как я много читаю, полагаю, что неплохо понимаю, за что можно поставить книге ту или иную оценку, как на это влияет количество страниц и прочее. Поэтому я выбрал именно эти данные.

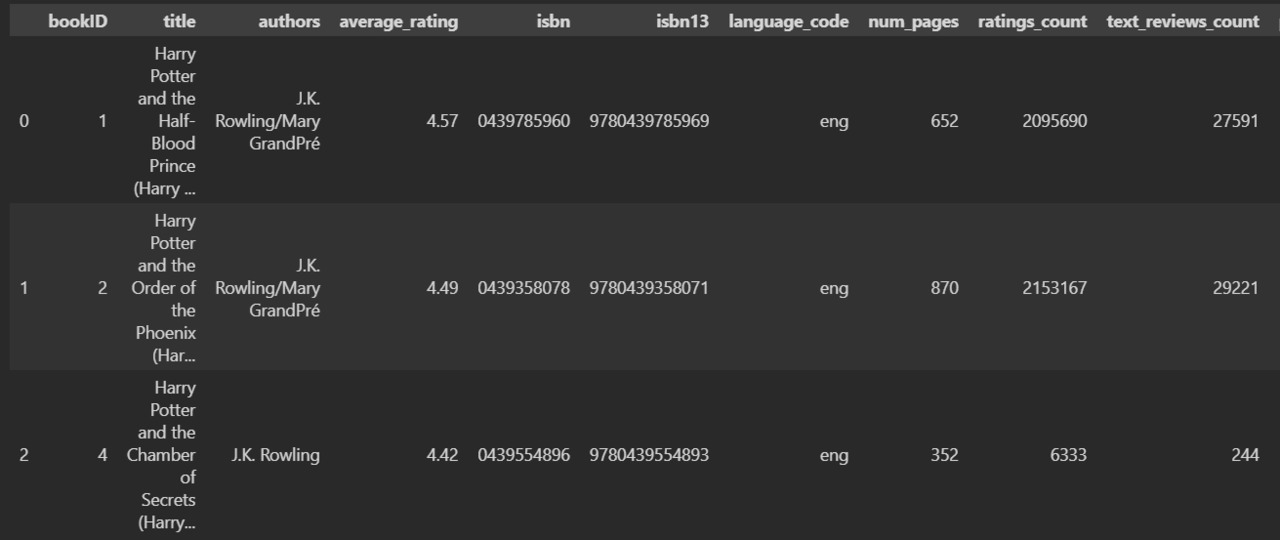
Вижу, что данные можно разбить на две категории:

1) сведения о книге (название, автор, isbn, язык, количество страниц, дата публикации и издательство);

2) сведения о реакции читателей (средний рейтинг, количество отзывов, количество оценок).

Данные рассказывают не просто про книгу и не просто про реакцию на книгу, а про реакцию читателей, измеренную конкретными признаками, на книгу, также измеренную конкретными признаками. Если у меня нет специального задания по анализу, то я могу наметить стратегию исследования по имеющимся признакам. Так, например, может быть интересно, каким книгам чаще ставят положительные оценки? как зависит оценка книги от количества страниц в ней?

Сформулирую для себя общую цель — изучить от чего зависит оценка книги.

Таблица задает две оси: вертикальная — наблюдения, горизонтальная — признаки.

Метка для наблюдений — индекс, метка для признаков — название признаков (название столбцов). Поэтому, естественно, что подготовка данных должна начинаться с обследования меток. Однако индекс формируется автоматически в порядке возрастания от 0 до n (это поведение по умолчанию можно изменить). Названия столбцов были предоставлены вместе с данными, поэтому их-то отдельно и надо обследовать.

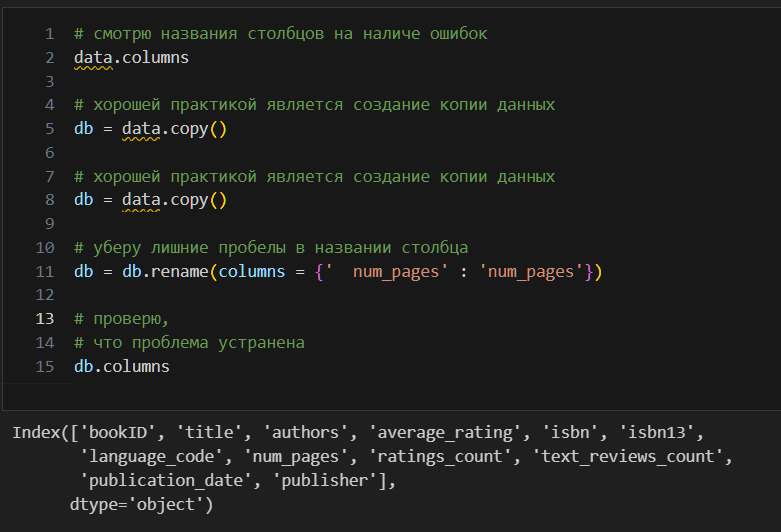
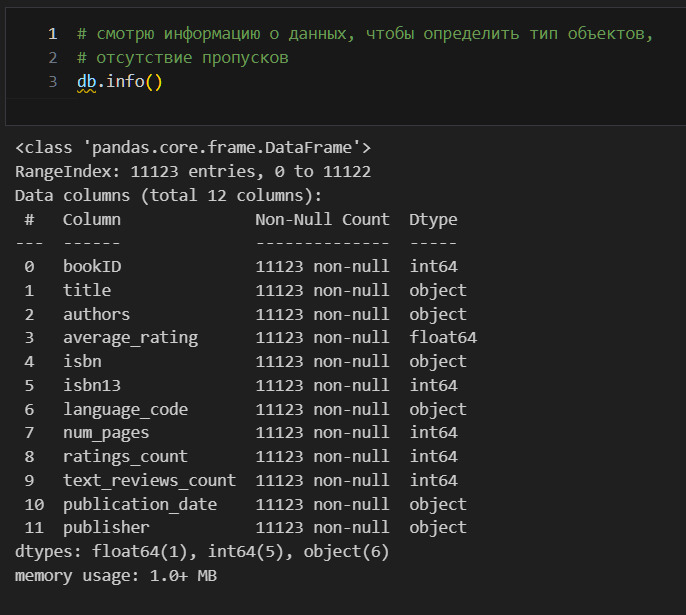
Вижу, что есть 12 признаков (нумерация начинается с 0 и продолжается до 11) и 11123 наблюдений (строк). Пропусков нет (количество объектов по столбцам одинаковое). Индекс у нас это RangeIndex. По типам данных заметно две проблемы. isbn помечен как объект, а isbn13 как int64. Кроме того, publication_date помечен как объект, хотя это очевидно дата. Изменю тип данных.

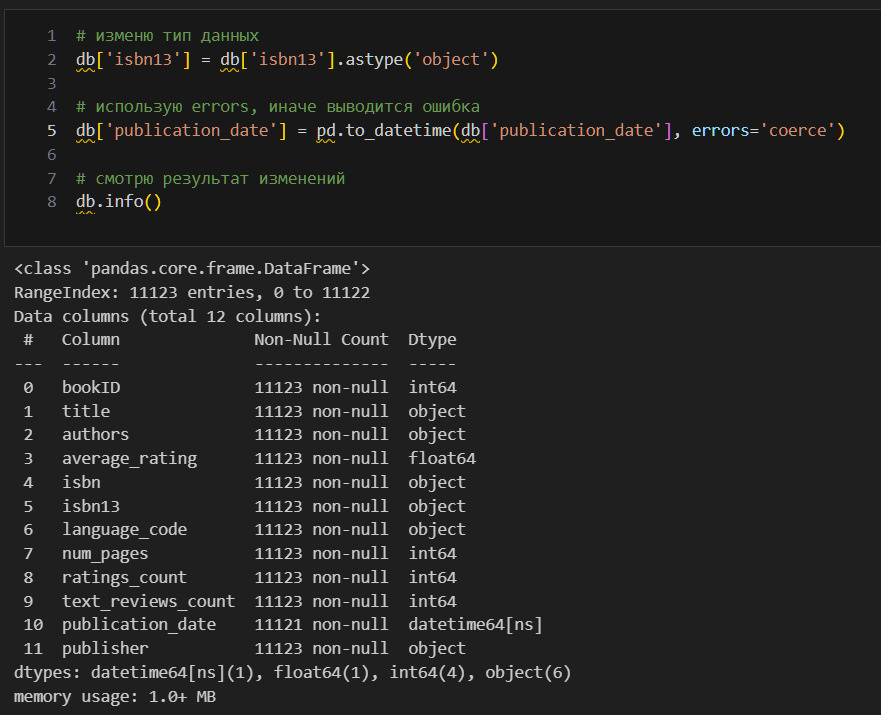
Вижу, что в publication_date появилось два пропущенных значения. Так как подобных строк всего две, я могу их удалить.

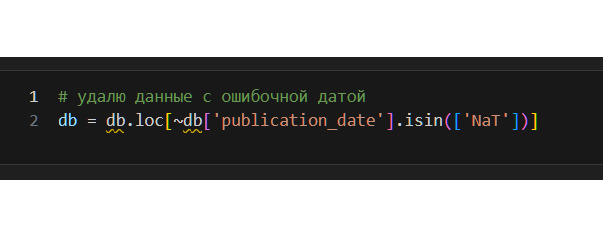
Запись выше надо читать так. В таблице db выбрать только те строки, у которых в столбце «publication_date» нет значения NaT. Значок тильды ~ означает «не». Метод isin проверяет наличие указанных данных в ячейке.

Здесь также важно, что я могу взять изначальную таблицу, отфильтровать ее, как мне это необходимо, а затем заменить изначальную таблицу отфильтрованной. Другими словами, изначально у меня была таблица db, после изменений я получаю таблицу с тем же названием db, но уже отфильтрованную.

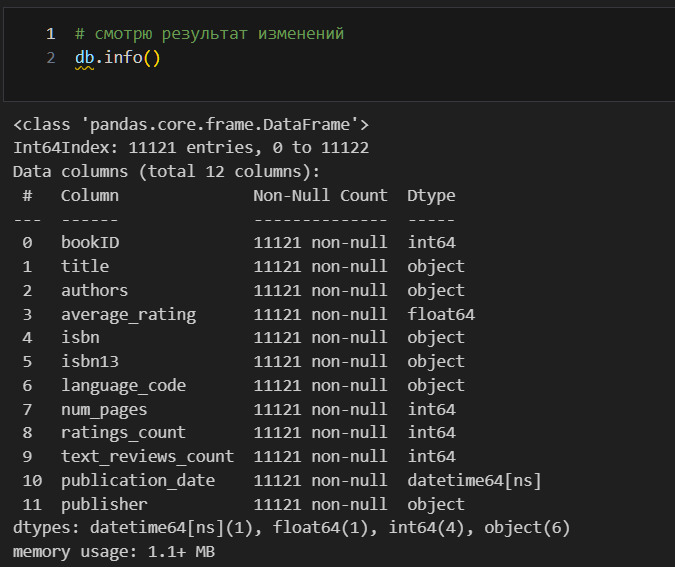
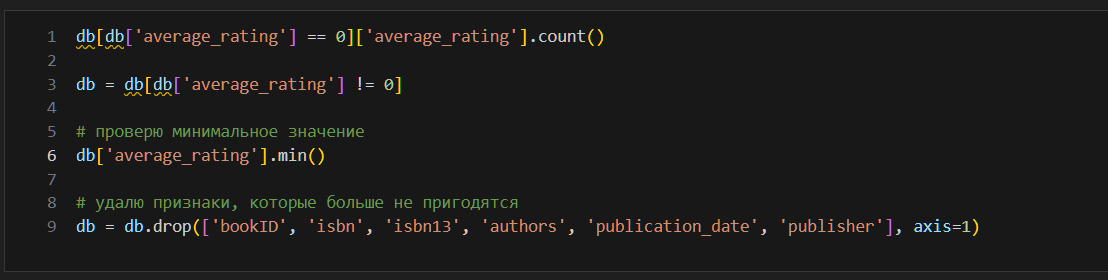
Теперь я должен заняться дубликатами строк. Я могу искать либо полные дубликаты (данные в каждом столбце для строки полностью совпадают), либо искать дубликаты выборочно. Здесь надо обратить внимание, что isbn является уникальным идентификатором каждой изданной книги. Поэтому логично искать дубликаты только по этому признаку, так как книги вполне могут совпадать по иным признакам и это нормально.

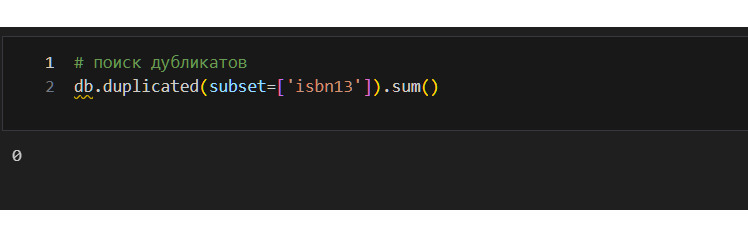
Дубликатов по isbn13 нет. Но все-таки посмотрю дубликаты по названию и имени автора.

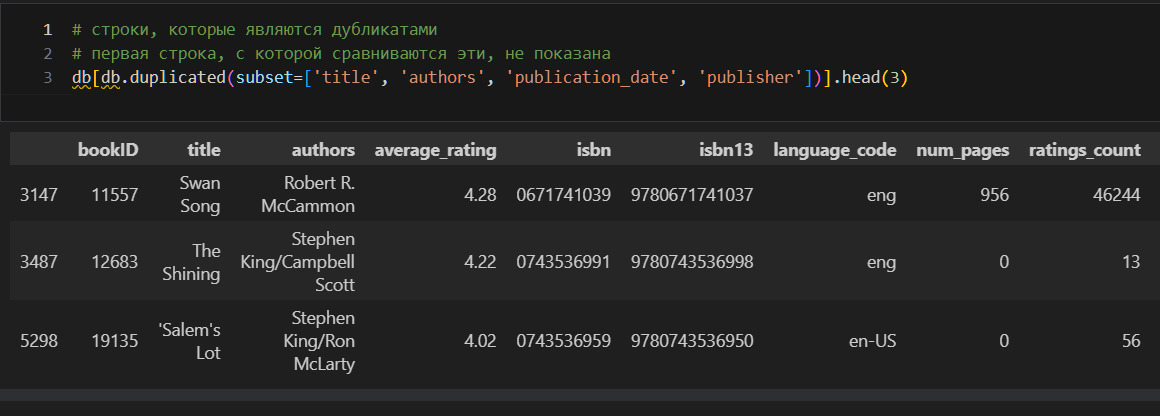
Такой подход позволяет понять, почему могут совпадать имя автора и название при различных isbn. Вижу, что, как правило, такие дубликаты — это аудиокниги. С этим придется разобраться отдельно. Для начала посмотрю, есть ли нулевое количество страниц у книг.

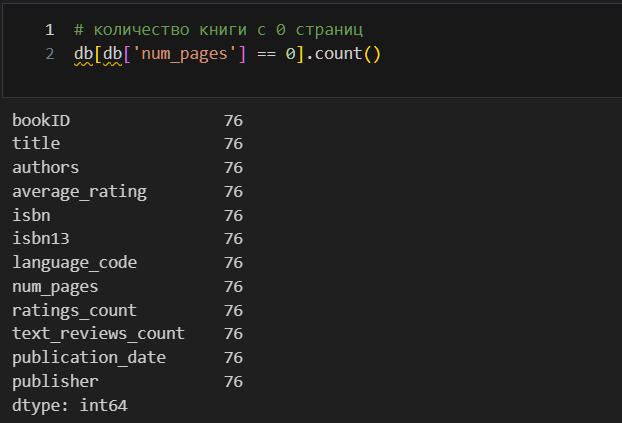
Таких книг 76. Что их объединяет? Посмотрю издательства.

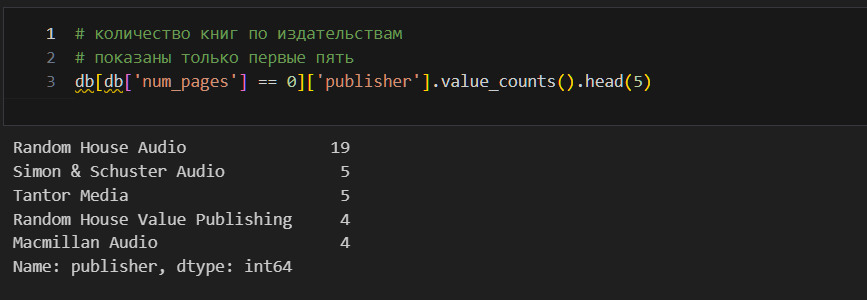
Вижу, что в основном это издательства, которые выпускают аудиокниги. Это логично. Если у книги нет страниц, то это просто аудиокнига. Но посмотрим количество страниц для тех книг, которые выпускали эти издательства.

Код выше весьма любопытен. Как его прочитать? Берем таблицу db. В этой таблице ищем такие строки, в которых столбец равен 0. Далее, в отфильтрованной таким образом таблице, берем столбец ’publisher’. После этого вызываем value_counts для подсчета количества и head для ограничения вывода результатов.

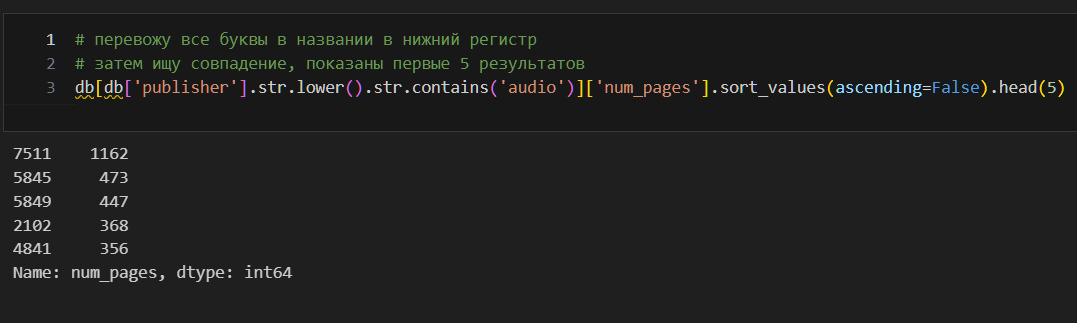
Вижу, что аудиоиздательства издают нечто, что имеет страницы, даже 1162 страницы! Посмотрю на это.

*Заметка к коду*

Код выше очень похож на предыдущий и может быть аналогично прочитан. Однако обращает внимание, что при первоначальной фильтрации таблицы я могу добавить дополнительные методы, например str и т. п.

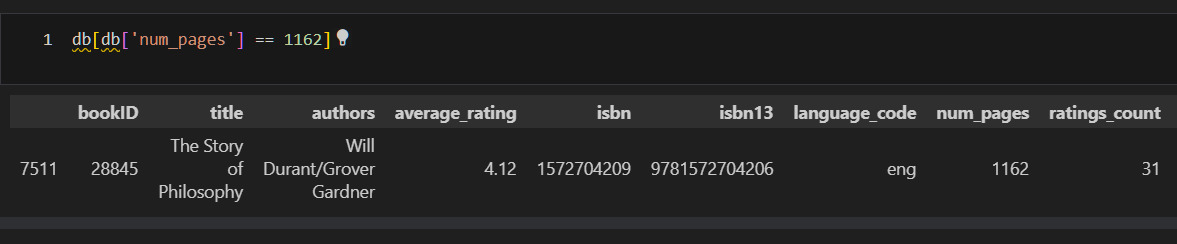
В интернете, например, на сайте Amazon, можно обнаружить эту книгу. И она оказывается аудиокнигой! Таким образом, количество «страниц» еще не говорит нам, что это бумажная книга. Это может быть, например, вес дисков. Более верный признак — это именно издательство. Как же поступить? Ведь сравнить книги аудио и бумажные по количеству страниц не получится. Следовательно, в одном признаке смешаны различные числа — количество страниц и вес дисков. Удалю все аудиокниги, но сначала сравню оценки по бумажным и аудиокнигам.

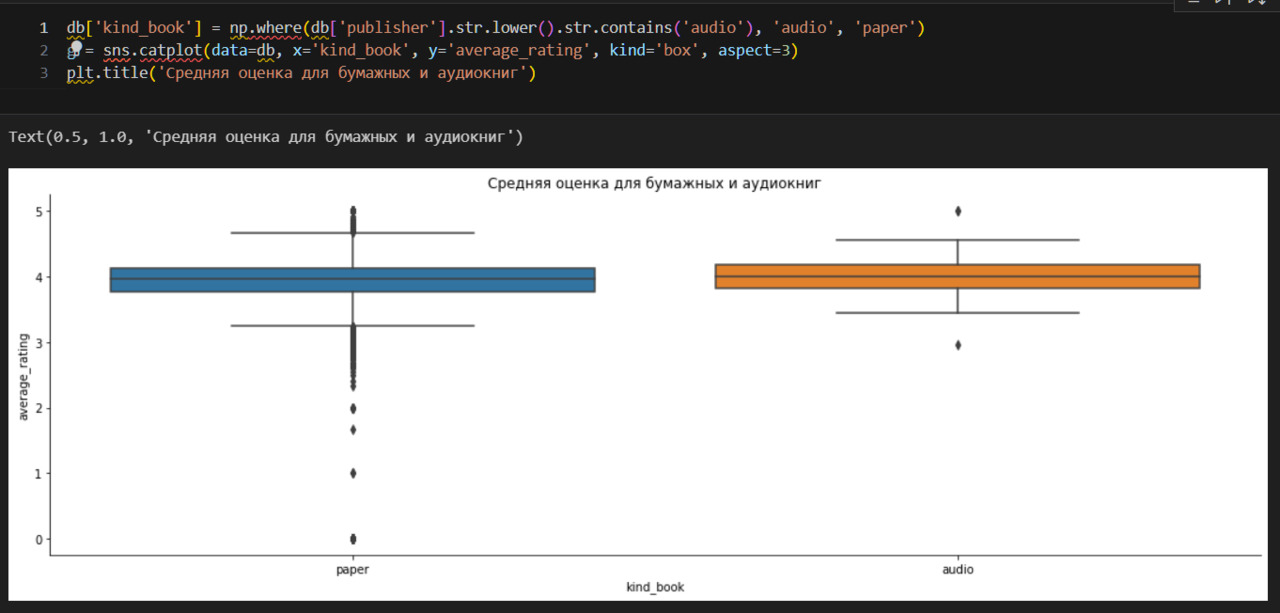
Вижу, что медиана не отличается, хотя разброс оценок для бумажных книг больше, чем для аудиокниг. Удалю вспомогательный признак, а также все аудиокниги. Надо учитывать, что такой подход, когда сравниваются две категории книг по графикам, является довольно грубым. Здесь бы стоило применить, например, t-тест. Но у меня нет специальной задачи исследовать аудио- и бумажные книги, поэтому ограничусь графиками.

*Заметка к коду*

Как прочитать np. where? Здесь я беру исходные данные признака, нахожу один из них, например названия с «audio», и присваиваю значение «audio», а если это не выполняется, то присваиваю значение «paper».

Еще раз посмотрю на таблицу, но выберу только количество страниц до 10. Посмотрю издательства.

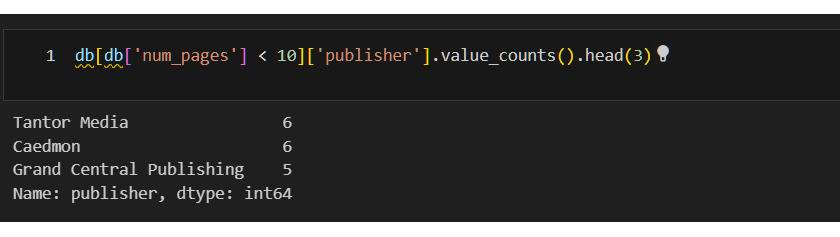
Если изучить полный список, то можно заметить, что там есть издательства Listening Library и ряд других, которые очевидно выпускают аудиокниги. Прихожу к выводу, что книги с количеством страниц 10 — это аудиокниги. Удалю их.

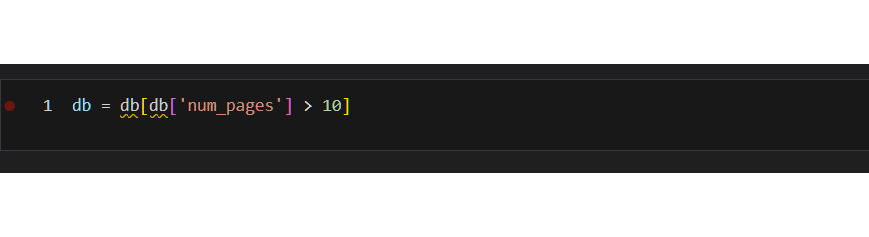
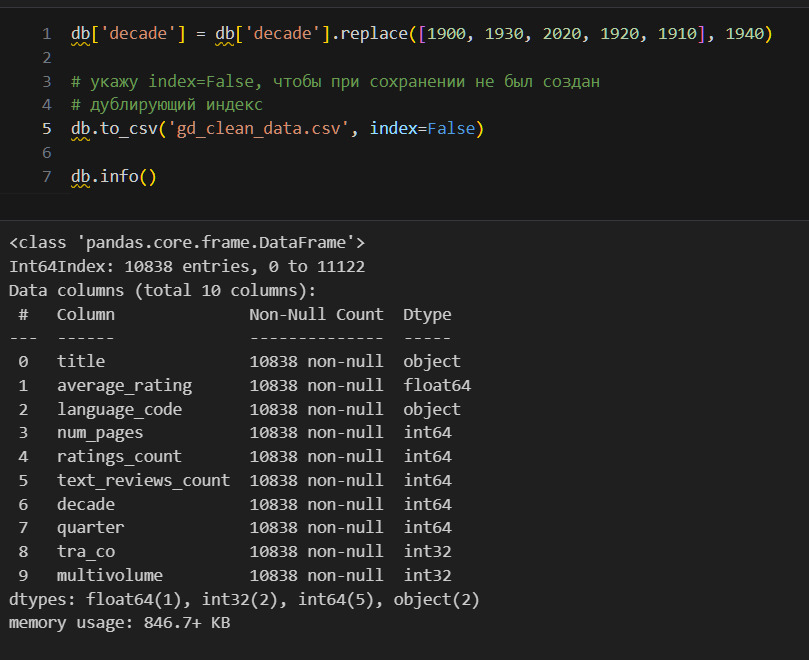
Добавлю два дополнительных признака в таблицу:

1) десятилетие, в котором вышла книга,

2) квартал, в котором вышла книга.

Это называется конструированием признаков, исходя из целей исследования. Специальных целей передо мной не ставили, я ищу их для себя сам. Меня будет интересовать, как распределяются книги по десятилетиям и в какой квартал их чаще выпускают. Почему именно эти признаки? Потому что десятилетия отражают развитие рынка книготорговли, изменение форматов и т. п. Кварталы же зависят от праздников, сезонности, что также может оказывать влияние на оценку книги.

Конструирование признаков возможно двумя путями:

1) самостоятельно определить новый признак,

2) признак создается автоматически, например простым возведением каждого числового признака в квадрат или перемножением каждой пары таких признаков.

Если затруднительно самостоятельно определить признаки, которые было бы интересно изучить, то можно применить второй метод. В этом случае можно и не создавать признаки на этапе обработки данных, можно использовать специальные методы, например полиномиальную регрессию.

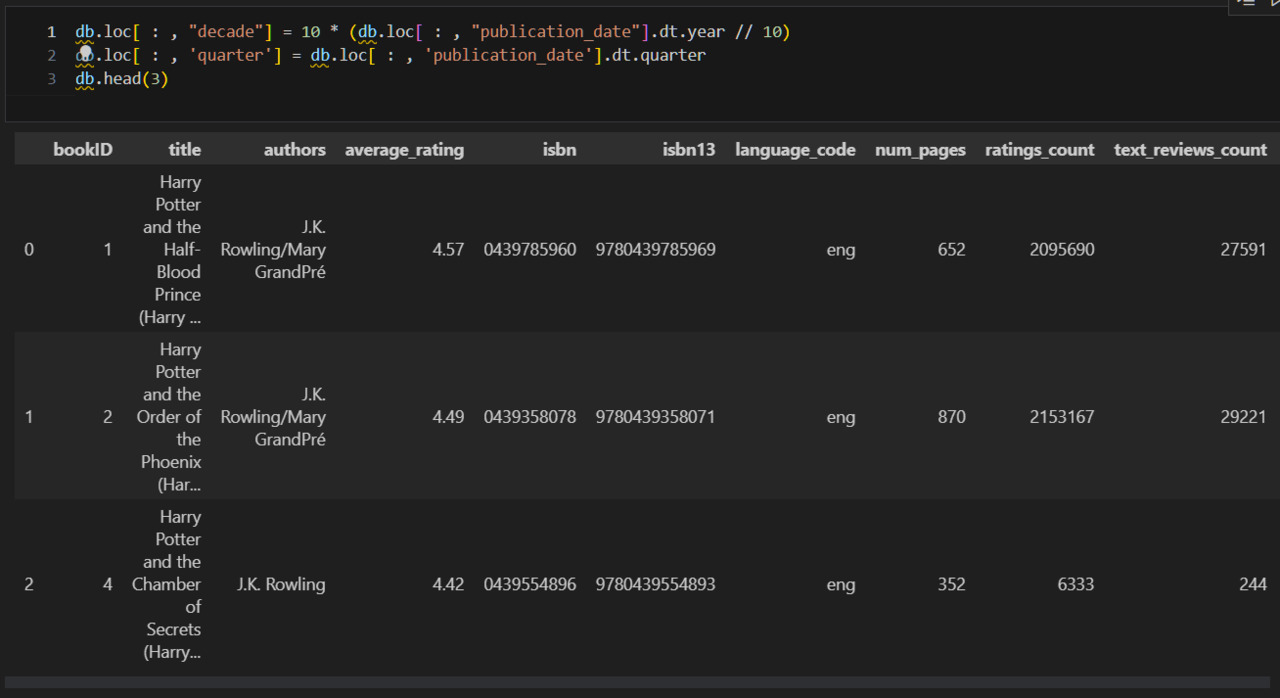
Теперь посмотрю на признак authors. Вижу, что здесь есть случаи, когда указано несколько имен через /. Сколько таких случаев?

*Заметка к коду*

Чтобы получить значение десятилетия, я использовал код 10 * (db. loc [:, «publication_date»].dt. year // 10). Почему? В этом коде я сначала делю год на 10, причем оставляю только целую часть. Например, если год 2001, то получаю 200. А затем уже умножаю на 10 это «целое» число, что и дает декаду.

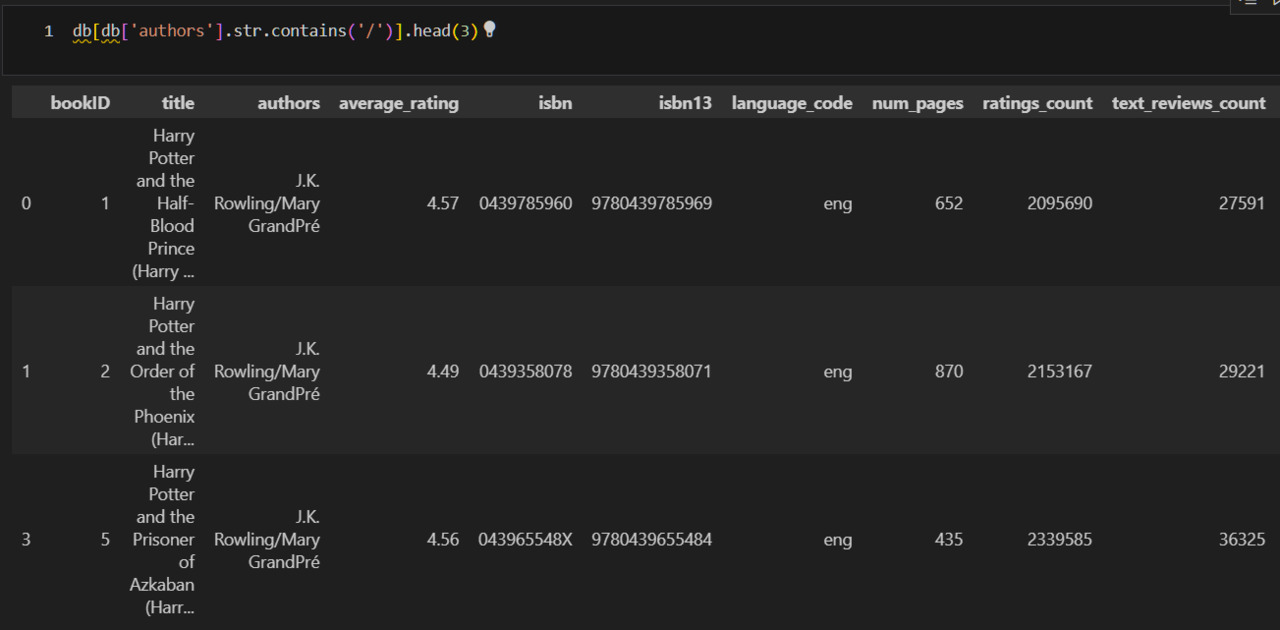
Из примеров видно, что, как правило, через слеш указаны переводчики. Однако возможны и другие ситуации. Это могут быть соавторы или вариант написания имени. Без дополнительного исследования внешних источников это определить нельзя. В этой ситуации можно сделать следующее. Заменю слеш на запятую. Создам колонку tra_co (переводчик или соавтор) и присвою 1 тем случаям, где есть запятая, и 0 остальным.

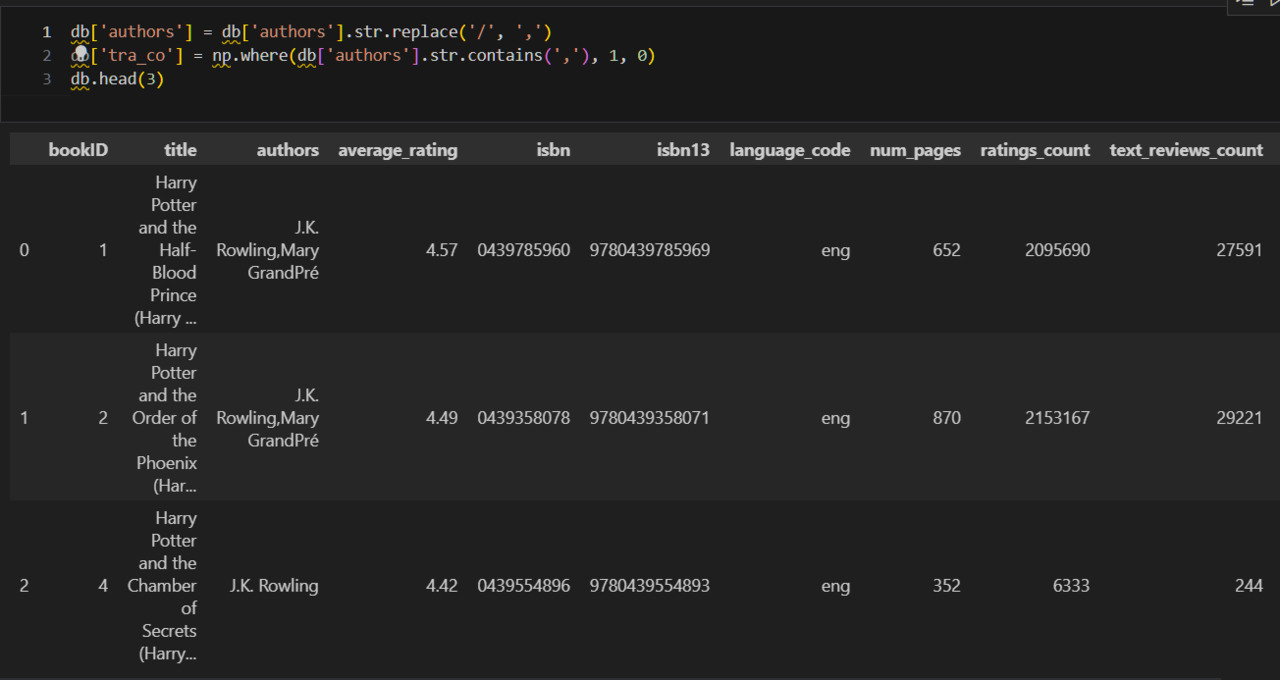
Теперь разберусь с книгами, у которых слишком большие значения количества страниц. Посмотрю на них повнимательнее.

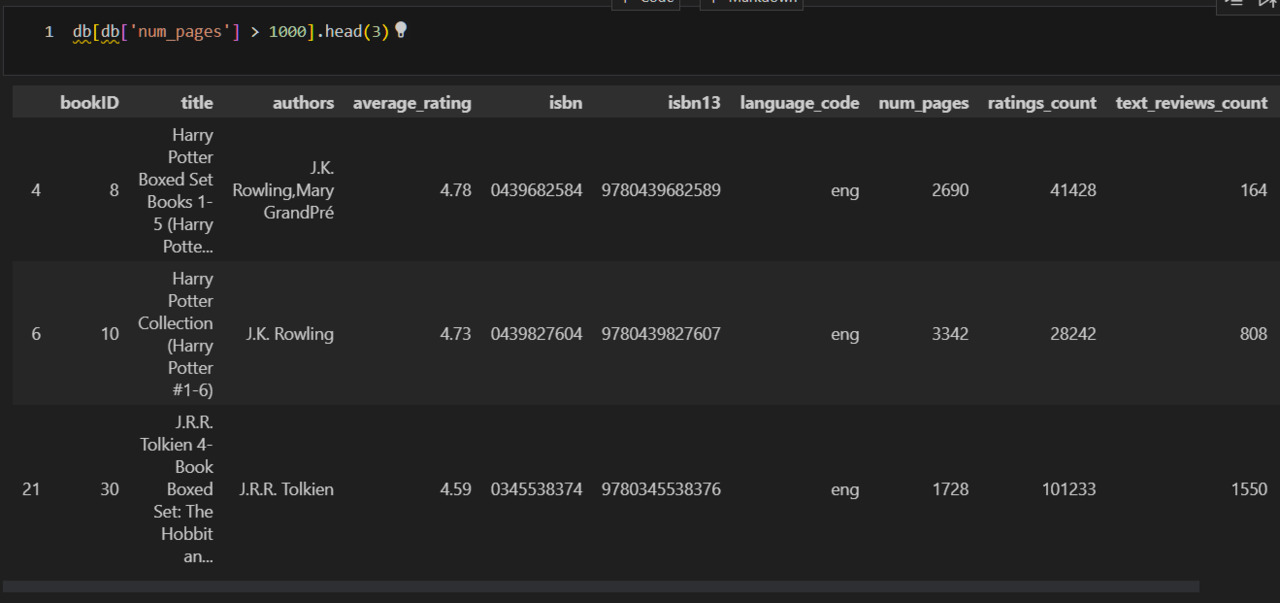
Как правило, книги с количеством страниц больше 1000 — это многотомные издания. Очевидно, что просто убрать такие книги, как я сделал с книгами, у которых было 0 страниц, нельзя. Что же тогда? Я должен найти все такие книги и пометить их. Для этого надо определить маркеры, которые позволят найти многотомные издания. Уже представленный выше список дает идеи:

1) книги с наличием знака #,

2) книги со словами Boxed Set.

Кроме того, под подозрением все книги со словами «books», «vol.», «volume», «series».

См. хорошее руководство по регулярным выражениям https://developers.google.com/edu/python/regular-expressions.

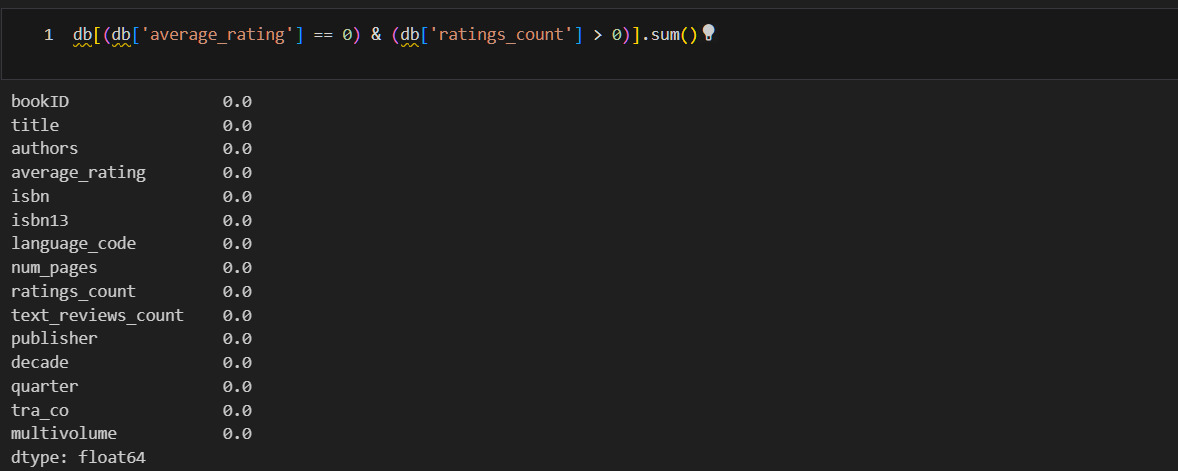
Минимальная оценка это 0. Но на сайте нельзя поставить такую оценку. Поэтому 0 означает отсутствие оценки, то есть это категориальный признак, который «пробрался» в числовой. Посмотрю количество и удалю, так как такое смешение недопустимо. Однако, если оценка 0, но количество оценок не 0, то это просто ошибка. Проверю это.

Удалю редкие категории. Для этого можно применить следующий код к каждой категориальной переменной.

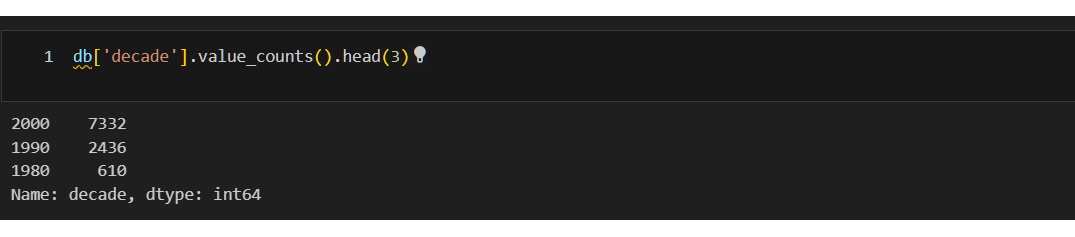
Здесь не привожу вывод по каждой категории. Однако общий вывод такой: редкие категории встречаются в **decade**, поэтому объединю все года, у которых менее 20 значений в год 1940.

Почему необходимо укрупнений категорий? Потому что маленькие категории несут мало информации, в то же время увеличение размерности данных ведет к тому, что известно как «проклятие размерности».

Глава 2. Статистическое исследование

Введение

Статистическое исследование данных может быть осуществлено двумя основными способами — это либо классический статистический анализ, либо то, что известно как Exploratory Data Analysis (EDA).

Понять отличие можно по следующим схемам.

Классический анализ идет по схеме: Проблема => Данные => Модель => Анализ => Выводы. В свою очередь EDA строится чуть иначе: Проблема => Данные => Анализ => Модель => Выводы.

Отличие в том, что в классическом подходе сначала идет модель, а затем анализ, а в EDA сначала анализ данных, а затем уже модель. Другими словами, классический анализ как бы навязывает определенную модель данным, в то время как EDA пытается по данным определить, какая модель больше подходит.

Как итог, в EDA больше используют графики, например гистограммы, ящики с усами и т. п. Классический же подход больше использует тесты, проверку гипотез. Например, это ANOVA, t-tests, chi-squared tests, и F-tests.

В этой методичке я использую элементы каждого из подходов. Поэтому я провожу деление всех способов статистического анализа на:

1) количественные (тестирование гипотез, анализ распределения и прочее);

2) графические (гистограммы, скаттерплоты и прочее).

Вот типичные вопросы, на которые старается ответить статистический анализ данных:

1) Какие значения являются типичными?

2) Каким распределением можно описать данные?

3) Как данный фактор влияет на целевой признак?

4) Какие факторы самые важные?

5) Есть ли в данных выбросы?

Важно всегда помнить, что большинство способов статанализа предполагает, что данные получены случайным образом. Если это предположение не выполняется, то результаты тестов, модели перестают быть достоверными.

Теперь еще раз, но уже больше с привязкой к данным. Статанализ (математическая статистика) работает с данными. Но что такое данные? Как правило, данные — это совокупность строк и столбцов. Пускай их будет только два. Вот такие например.

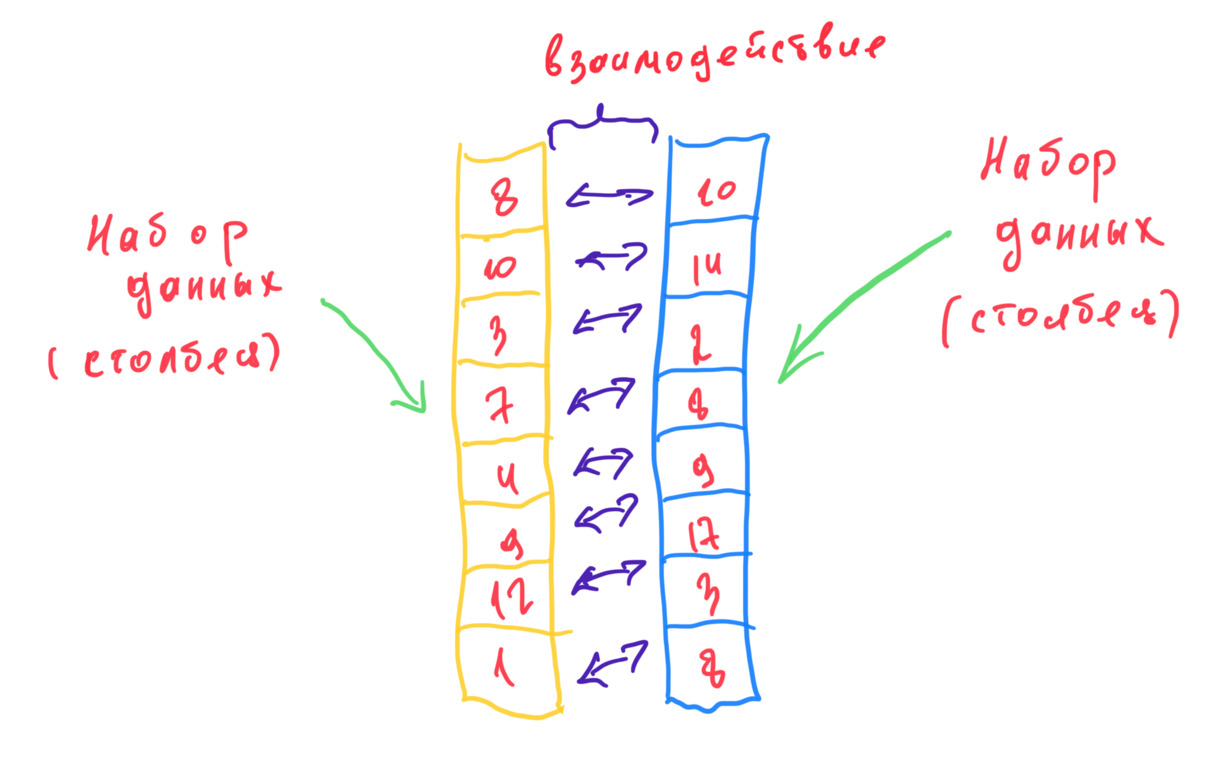
Что я могу с этим сделать? Как я могу «раскрутить», «покрутить» эти данные? Я могу, например, заинтересоваться только одним из столбцов. Какое среднее значение? А как отличаются от среднего фактические значения? Насколько вероятно появление одного из значений или нового значения? Но меня может заинтересовать и взаимодействие столбцов. Если растет значение в одном столбце, то растет ли значение в другом? Связаны ли эти столбцы? И если связаны, то насколько сильно? И вот еще что важно. Данные по Goodreads, которые я здесь использую, — это только небольшая выборка всех книг, изданных в мире. Поэтому те данные, которые видны выше на рисунке, — это тоже только выборка из генеральной совокупности. А раз так, то стоит также задача оценить по этим выборочным данным генеральную совокупность (или же наоборот, если известны характеристики генеральной совокупности).

Все это можно сделать со столбцами. И математическая статистика как раз пытается ответить на вопросы выше. Итак, математическая статистика:

1. дает математическое описание набора данных (столбца);

2. определяет вид распределения (для определения вероятности новых значений и не только);

3. дает описание того, как взаимодействуют два и более набора данных (столбцы).

Глядя на рисунок выше надо также учитывать, что, как правило, набор данных далеко не отражает всех данных. Например, в данных Goodreads приведена только небольшая выборка из всех книг. Это ставит перед математической статистикой дополнительные задачи.

В качестве учебника по математической статистике я рекомендую учебник Гмурмана «Теория вероятностей и математическая статистика» (далее — Гмурман). Вот как этот автор описывает, чем занимается матстат (стр. 187 Гмурман):

1. «оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого неизвестен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.»;

2. «проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого неизвестен».

Некоторые важные концепции математической статистики

«Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности» (Гмурман, стр. 76).

Математическое ожидание примерно равно среднему значению. Причем «математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины» (Гмурман, стр. 78). Поэтому — чем больше данных, тем лучше.

Понятие «центрированная величина» возникает из-за того, что такая величина получается как «разность между случайной величиной и ее математическим ожиданием» (Гмурман, стр. 87). Само же математическое ожидание принимается за центр распределения набора данных.

«Дисперсией (рассениянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания» (Гмурман, стр. 88).

Вот формула:

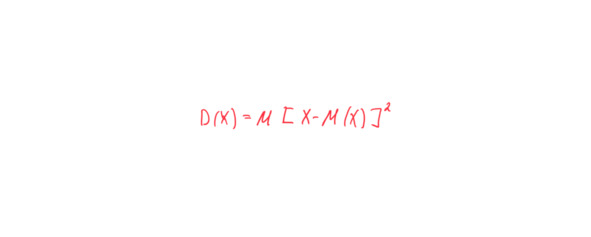
В этой записи надо учитывать, что прописная X означает весь набор данных, например 3, 8, 19 и т. д. То есть формулу надо читать так, что из каждого из единичных значений X производится вычитание. Например, вычитаем матожидание из 3, из 8, из 19 и т. д.

Подробнее про компоненты дисперсии можно посмотреть в учебнике для инженеров [7.4.4. What are variance components?] (https://www.itl.nist.gov/div898/handbook/prc/section4/)

Совет

«В тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в линейных метрах, то среднее квадратическое отклонение будет также выражаться в линейных метрах, а дисперсия — в квадратных метрах» (Гмурман, стр. 94).

Теперь разберу концепцию начальных и центральных моментов, очень важную для математической статистики. Для этого возьму произвольный набор данных, в котором для каждого значения известна вероятность.

Вот как считается математическое ожидание:

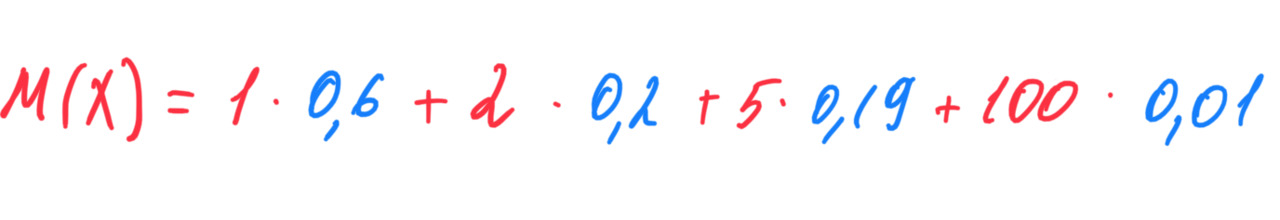
Еще раз, важно запомнить, что в записи M (X) вот это X означает случайную величину, скажем измерения линейкой. Отдельное значение из этой случайной величины (верхняя строка в таблице выше) обозначается как x. Когда же есть запись с X, то имеются ввиду все значения x.

Итак, теперь возведу в квадрат случайную величину.

Вероятность не изменилась. Это можно понять так. Возведением в квадрат изменяется масштаб, но не вероятность. Каким будет математическое ожидание?

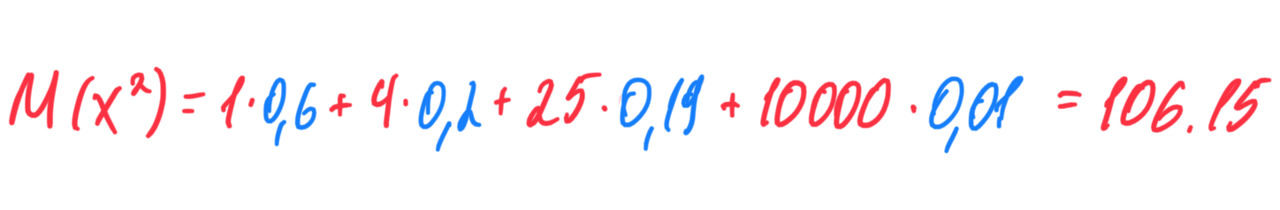
Какой вывод я могу сделать? Второе математическое ожидание гораздо больше первого. Почему? Потому что в первом случае я умножал вероятность 0,01 на 100, а во втором ту же вероятность 0,01 я умножил уже на 10000. Это позволило «лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность» (Гмурман, 98). В зависимости от количества подобных величин, того, насколько они «маленькие», может потребоваться возведение не только в квадрат, но и в более высокие степени.

Начальным моментом порядка k называют математическое ожидание случайной величины, возведенной в степень (k, это может быть и степень k=1). Центральным моментом порядка k называют математическое ожидание степени разности между случайной величиной и математическим ожиданием случайной величины.

[Не так строго понять это можно следующим образом. Сначала я нахожу среднее значение набора данных (это будет математическим ожиданием). Затем я вычитаю из каждого значения набора данных это среднее значение. У меня получится новый набор данных. Теперь я могу найти среднее этого нового набора данных (это также будет математическим ожиданием, но для нового набора данных).]

Применение закона больших чисел разъясняется в главе 9 Гмурмана. Здесь я не буду останавливаться на этом подробнее.

Выборкой «называют совокупность случайно отобранных объектов» (Гмурман, стр. 188). Выборка осуществляется по специальным правилам. Подробнее об этом можно узнать здесь (https://www.itl.nist.gov/div898/handbook/ppc/section3/ppc333.htm), а также в [7.2.4.2. Sample sizes required] (https://www.itl.nist.gov/div898/handbook/prc/section2/prc242.htm).

Генеральной совокупностью «называют совокупность объектов, из которых производится выборка» (там же).

В теории вероятностей

«под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике — соответствие между наблюдаемыми вариантами и их частотами или относительными частотами» (Гмурман, стр. 192).

В случае, который разбираю я на данных Goodreads, имеющиеся у меня данные — это выборка, по которой я хочу оценить генеральную совокупность — все книги на сайте Goodreads.

Вот как это работает.

«Пусть требуется изучить количественный признак генеральной совокупности. Допустим, что из теоретических соображений удалось установить, какое именно распределение имеет признак. Естественно возникает задача оценки параметров, которыми определяется это распределение. Например, если наперед известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (приближенно найти) математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение; если же есть основания считать, что признак имеет, например, распределение Пуассона, то необходимо оценить параметр лямбда, которым это распределение определяется» (Гмурман, стр. 197).

Например, генеральная совокупность — все книги на Goodreads. Параметр, который нас интересует, — это количество страниц. Количество страниц в каждой книге Goodreads — это и есть количественный признак генеральной совокупности.

Итак, есть оцениваемые параметры, а есть статистические оценки таких параметров. Такие оценки должны соответствовать определенным требованиям. Буду делать выборки из генеральной совокупности книг. Для каждой выборки оценю параметр, например среднее значение страниц в книге. Каждая такая выборка даст свое значение, совокупность таких значений и будет набором данных, у которого также может быть математическое ожидание (среднее). Отсюда появляется понятие несмещенной оценки.

«Несмещенной называют статистическую оценку, математическое ожидание которой равно оцениваемому параметру при любом объеме выборки» (Гмурман стр. 198).

Соответственно, если оценка не соответствует указанным свойствам, то она является смещенной.

Вот еще пояснение из учебника «Теория и методы эконометрики», авторов Дэвидсона, Мак-Кинона (далее — Дэвидсон), который я также рекомендую.

«На интуитивном уровне это означает, что если мы станем использовать метод оценивания, дающий несмещенные оценки для расчета оценок по очень большому числу выборок, то среднее значение получаемых с его помощью оценок будет приближаться к оцениваемой величине. При прочих равных статистических свойствах двух методов оценивания несмещенный метод всегда предпочтительнее смещенного».

Однако, даже если оценка является несмещенной, все-таки дисперсия в наборе данных, на основе которых посчитана оценка, может быть большой. Поэтому еще одним требованием к оценке является эффективность.

«Эффективной называют статистическую оценку, которая (при заданном объеме выборки n) имеет наименьшую возможную дисперсию» (Гмурман, стр. 199).

Кроме того, если количество объектов в выборке стремится к бесконечности, то устанавливают требование о состоятельности.

«Состоятельной называют статистическую оценку, которая при [стремлении количества объектов к бесконечности] стремится по вероятности к оцениваемому параметру».

Про доверительные интервалы см. параграфы 14—16 гл. 16 Гмурмана.

Отдельные важные концепции математической статистики можно изучить по следующим ссылкам:

1. Про виды распределений — гл. 4 Дэвидсона. Хорошая галерея графиков с видами распределений находится здесь (https://www.itl.nist.gov/div898/handbook/eda/section3/eda366.htm), там же можно найти компактное описание распределений. Еще одно описание можно найти в том же учебнике [8.1.6. What are the basic lifetime distribution models used for non-repairable populations?] (https://www.itl.nist.gov/div898/handbook/apr/section1/apr16.htm). Почему важно правильно определить вид распределения? Потому что от этого зависит как применение тестов, так и проверка гипотез. Распределения также применяются для определения доверительных интервалов.

Подробнее остановлюсь на нормальном распределении.

Нормальное распределение определяется двумя параметрами: математическим ожиданием (a) и средним квадратическим отклонением. Про график нормального распределения, который выглядит как колокол и близок к приведенному выше, нужно помнить три правила:

1) «Изменение величины параметра a (математического ожидания) не изменяет форму нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ox: вправо, если a возрастает, и влево, если a убывает» (Гмурман, стр. 131).

2) «С возрастанием параметра средего квадратического отклонения максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, то есть сжимается к оси Ox; при убывании — нормальная кривая становится более „островершинной“ и растягивается в положительном направлении оси Oy» (там же).

3) Площадь под кривой всегда остается равной 1.

[Математическое ожидание показывает среднее значение в наборе. Поэтому, если такое среднее значение «двигается», то двигается и график, который построен ведь вокруг этого среднего значения. Среднее отклонение показывает разброс отдельных значений данных вокруг среднего. Если такой разброс увеличивается или уменьшается, то соответственно изменяется и график.]

В связи с нормальным распределением есть центральная предельная теорема (теорема Ляпунова). Вот ее формулировка:

«Если случайная величина X представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то X имеет распределение, близкое к нормальному» (Гмурман, стр. 135).

Таким образом, все распределения оцениваются применительно к нормальному. Поэтому нужны инструменты, которые бы показывали, что данное распределение отличается и насколько отличается от нормального. Для этого используют показатели эксцесса и ассиметрии. Для нормального распределения ассиметрия и эксцесс равны нулю. Если у данного набора эти значения сильно больше 0, то его распределение тем сильнее отличается от нормального, и наоборот. Ниже я покажу также иные способы определения нормальности распределения.

2. Проклятие размерности — гл. 2 «Основы статистического обучения» Тревор Хасти, Роберт Тибширани, Джером Фридман. Важность этой проблемы можно понять из следующей цитаты тех же авторов:

«С увеличением размерности сложность функций многих переменных может расти экспоненциально, и если мы хотим иметь возможность оценивать такие функции с той же точностью, что в пространствах малой размерности, то нам необходимо, чтобы размер нашего обучающего множества также рос экспоненциально» (стр. 24 английского издания).

Здесь же объясняется разложение среднеквадратической ошибки (MSE) на дисперсию и смещение. Привожу только вывод формулы для примера:

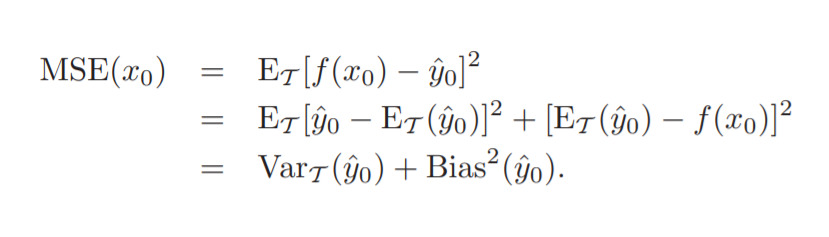
В учебнике Машинное обучение указывается следующее.

«В контексте моделей МО [машинного обучения] дисперсия измеряет постоянство (либо изменчивость) прогноза модели для классификации отдельного образца при многократном обучении модели, например, на разных подмножествах обучающего набора данных. Мы можем сказать, что модель чувствительна к случайности обучающих данных. Напротив, смещение измеряет, насколько далеко прогнозы находятся от коррективных значений в целом при многократном обучении модели на разных обучающих наборах данных; смещение представляет собой меру систематической ошибки, которая не является результатом случайности».

3. Z-оценка часто используется, например для определения выбросов. Вот формула для расчета:

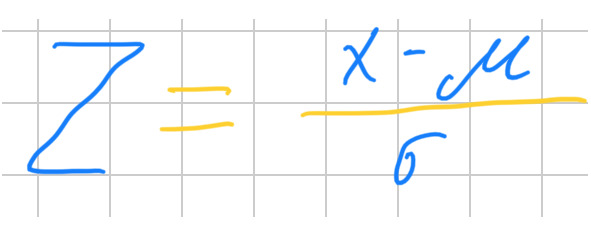
В этой формуле: x — это единичное значение из набора данных; мю — среднее набора данных; сигма — стандартное отклонение.

4. Доверительные интервалы, см. подробнее в [1.3.5.2. Confidence Limits for the Mean] (https://www.itl.nist.gov/div898/handbook/eda/section3/eda352.htm)

5. Дисперсия, ковариация, корреляция. Разница между дисперсией, ковариацией и корреляцией:

1) дисперсия — это мера изменчивости конкретного значения от среднего значения по всему набору данных;

2) ковариация — это мера взаимосвязи между изменчивостью двух переменных. Ковариация зависит от масштаба, поскольку она не стандартизирована;

3) корреляция — это связь между изменчивостью двух переменных. Корреляция стандартизирована, что делает ее не зависящей от масштаба.

Справочное руководство [Engineering statistics handbook] (https://www.itl.nist.gov/div898/handbook/eda/eda.htm) содержит пример схемы анализа данных:

1. Посчитать базовые статистики:

a) среднее;

b) стандартное отклонение. При этом надо помнить следующие эмпирические правила. Приблизительно 60—78% данных находятся в пределах одного стандартного отклонения от среднего. Приблизительно 90—98% данных находятся в пределах двух стандартных отклонений от среднего. Более 99% данных находятся в пределах трех стандартных отклонений от среднего;

c) коэффициент автокорреляции для проверки данных на случайность;

d) коэффициенты корреляции, коэффициенты, показывающие, что распределение является нормальным, например Wilk-Shapiro test.

2. Построить график для нормального распределения.

3. Линейная аппроксимация данных в зависимости от времени для оценки дрейфа (тест на фиксированное положение).

4. Тест Барлетта для дисперсии.

5. Критерий Anderson-Darling для нормального распределения.

6. Теста Граббса для определения выбросов.

Можно ознакомиться с примером анализа по указанной схеме [1.4.2.1.3. Quantitative Output and Interpretation] (https://www.itl.nist.gov/div898/handbook/eda/section4/eda4213.htm)

Загрузка и описание данных

Теперь мне надо определить, что я хочу узнать из данных. Специальных целей передо мной никто не ставил, поэтому определю их самостоятельно. Что интересного могут рассказать данные? Здесь же я сразу укажу, какими методами буду решать эти задачи. Надо помнить, что не всегда можно заранее знать, какой метод подойдет. Например, мне нужно сначала проверить распределение на нормальность, чтобы применить корреляцию. Поэтому в этот список можно вносить изменения по ходу анализа.

Как указывалось ранее, я могу разделить статистическое обследование на изучение набора данных и изучение отношений между наборами данных. С учетом этого и разделю задачи.

Изучение каждой группы данных отдельно:

* Характеристики центрального положения для количественных признаков. Метод describe;

* Характеристики категориальных данных. Тот же describe;

* Какой тип распределения у средних оценок для книг, для количества страниц в книгах? (здесь не рассматривается).

Изучение отношений между группами данных:

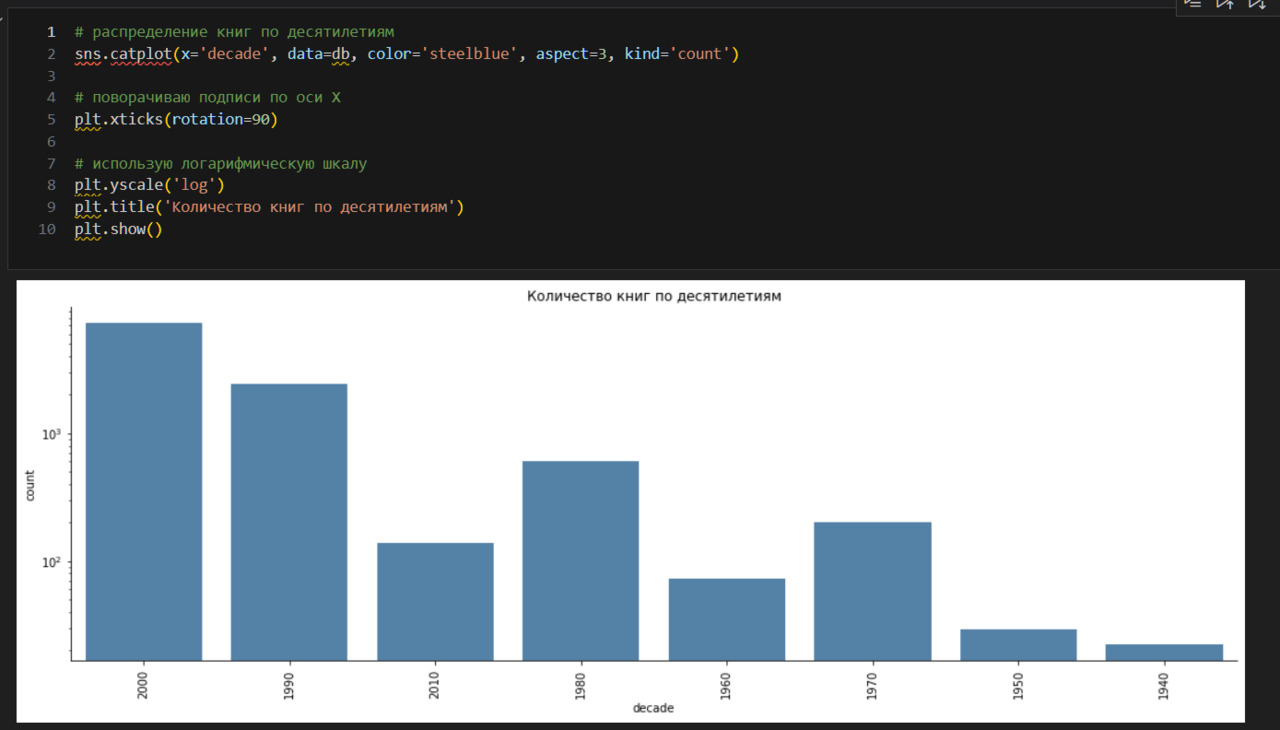
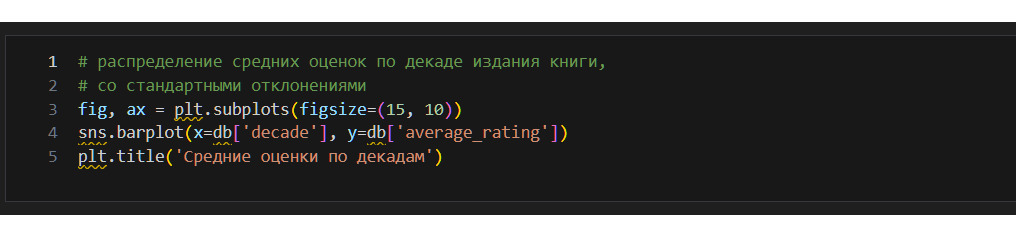
* Как распределены книги по десятилетиям? Использую график;

* Какие книги получили высокие оценки? Использую график;

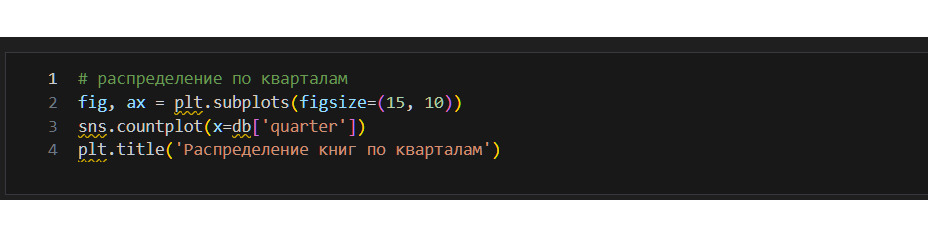
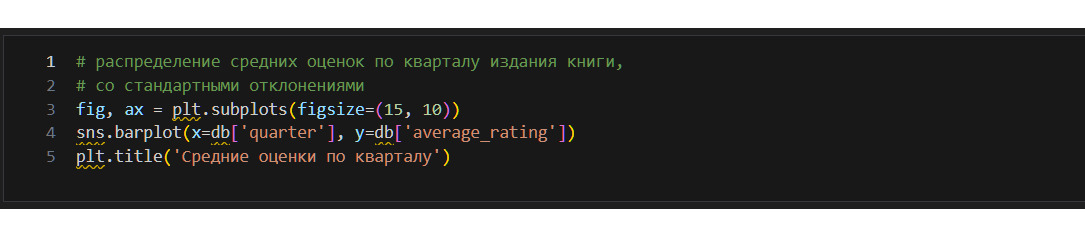
* Как распределены книги по кварталам? Использую график;

* Какие книги чаще всего издавались в рамках набора данных? Использую график;

* Если у книги есть соавтор или переводчик, как это влияет на оценку? Использую дисперсионный анализ;

* От каких признаков зависит оценка книги? Использую корреляцию, дисперсионный анализ;

* Какие слова чаще всего используются в названии книги? Использую NLTK.

Начну с характеристик центрального положения.

Я буду для простоты писать «статистика» вместо «математическая статистика», «статистический анализ», хотя строго говоря это не одно и то же.

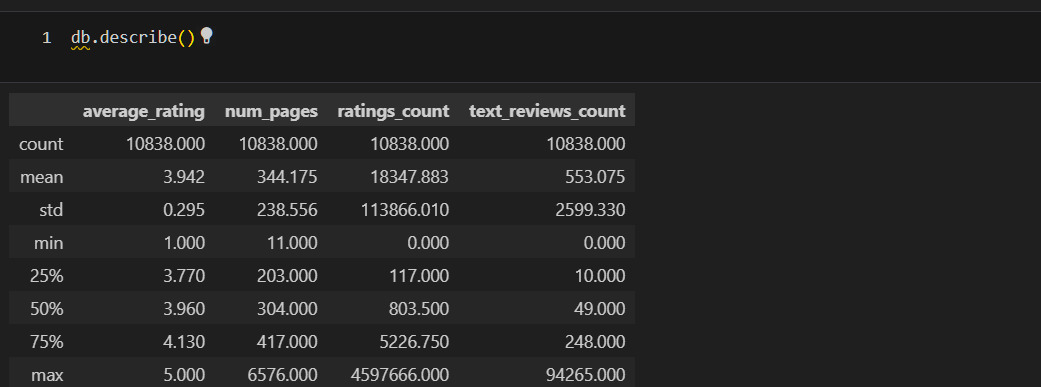
Уже в этой таблице можно видеть важнейшие концепции статистики. Выше я писал, что статистика должна описывать наборы данных и их взамиодействие. Здесь мы видим описание именно наборов данных, взаимодействие будет позже.

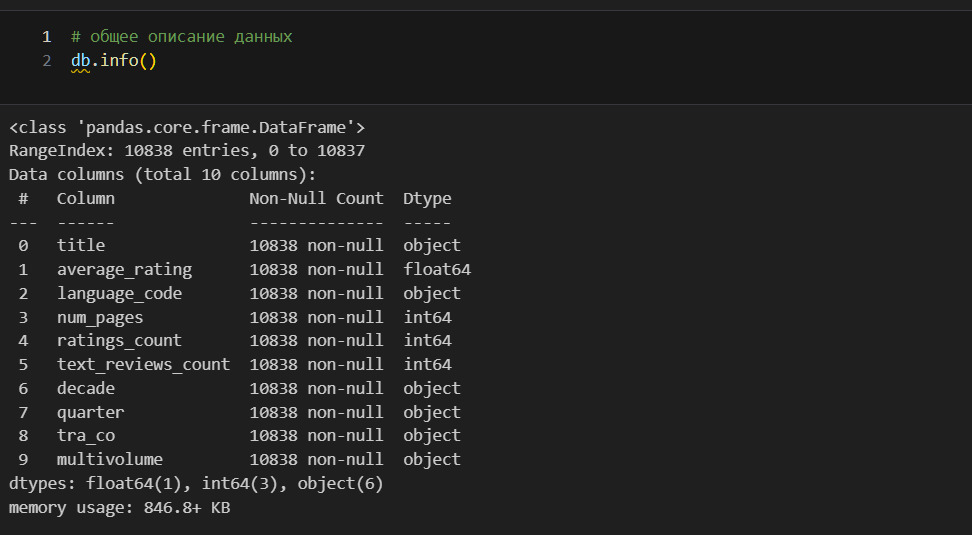
В таблице дается описание для четерых численных признаков: average_rating, num_pages, ratings_count, text_reviews_count. Остальные признаки являются категориальными и в эту таблицу не попали, но ниже я также рассмотрю и эти признаки. Пока продолжу изучать таблицу. Для каждого признака, например для text_reviews_count, приведен ряд характеристик (метрик): count, mean и т. д. Об этих характеристиках можно говорить как о характеристиках центрального положения. Откуда пошло такое выражение? Это показано на рисунке ниже

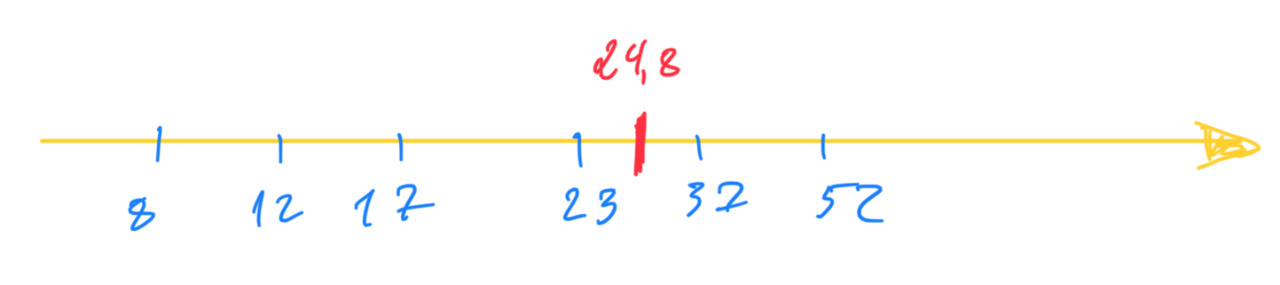
Среднее значение 24,8 есть характеристика центрального положения, так как фактические данные (8,12…52) расположены вокруг этого среднего. Отсюда же видно, например, что можно посчитать расстояние от центра до каждого значения, что приводит к дисперсии и стандартному отклонению.

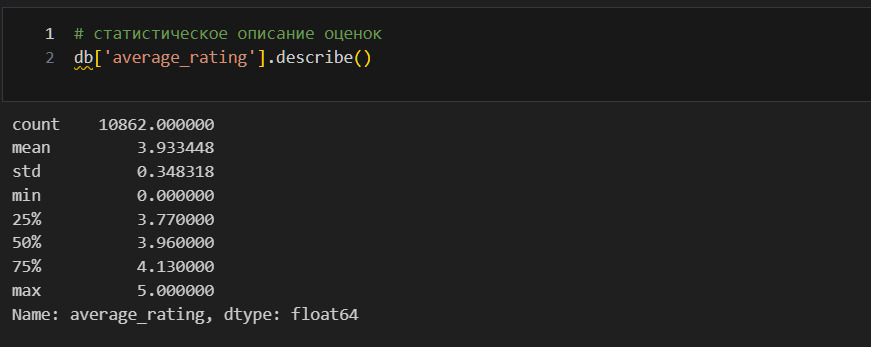
В чем смысл таких характеристик? У меня есть набор данных. Я хочу его как-то охарактеризовать. Зачем? Во-первых, чтобы лучше понять объект, который описывается этими данными. Например, про среднюю оценку я теперь знаю, что она у книг составляет 3.9. Во-вторых, чтобы уметь предсказывать будущие события. Например, я хочу знать, а какую оценку поставят новой книге. При прочих равных можно считать, что эта оценка будет близка к среднему значению. Но так как точно сказать этого нельзя, то меня интересует, в каком диапазоне может быть эта оценка, здесь помогает std. Минимум и максимум определяют, в каких границах расположены оценки. Благодаря этому я достоверно знаю, что оценка не может быть меньше 1 и не может быть больше 5. А к чему же все эти проценты: 25%, 50%, 75%? Эти проценты показывают следующее: 25% оценок ниже чем 3.77, 50% оценок ниже чем 3.96 и т. д. Это условно можно представить как вероятность: вероятность того, что оценка книги будет 3.77 составляет 25%.

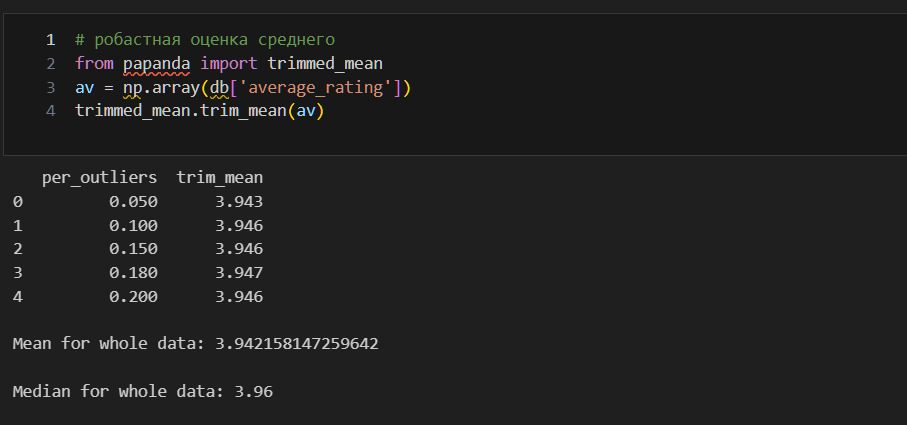
Так я изучаю характеристики каждого набора данных. Замечаю, что в num_pages, ratings_count, text_reviews_count есть странности. Так, например, среднее в num_pages составляет 344, но максимальное значение 6576. Говоря иначе, в среднем в одной книге 344 страницы, но есть книга, у которой 6576 страниц. Это может свидетельствовать о выбросах в данных. Непосредственно о выбросах я расскажу позже, но уже сейчас надо это учитывать. Если я предполагаю, что в моем наборе данных есть выбросы, то я могу использовать робастные, то есть устойчивые к выбросам методы оценки среднего. Я могу найти такую оценку с помощью библиотеки papanda.

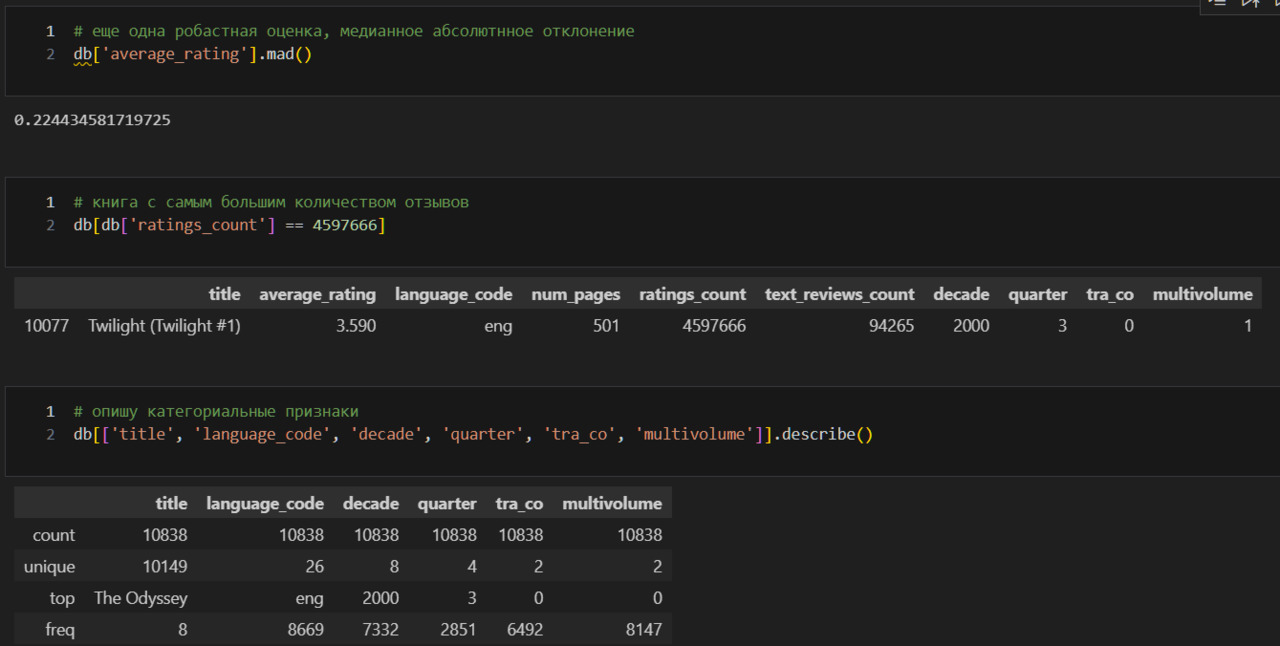
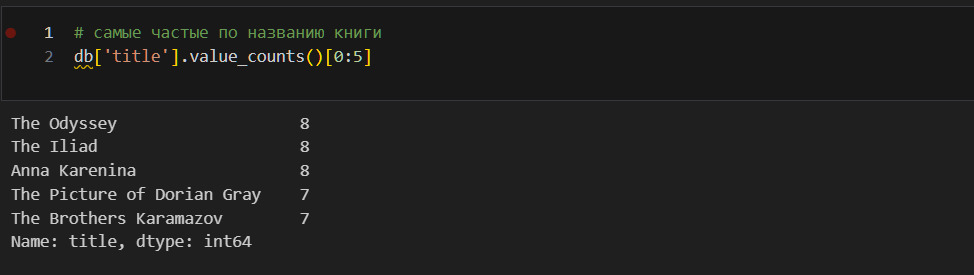
Вижу, что в данных 10149 уникальных названий книг из 10838.

Чаще всего встречается The Iliad, 8 раз. Однако надо учитывать, что есть еще несколько книг, которые в изданы 8 раз. Например, Анна Каренина. Поэтому The Iliad можно считать случайным.

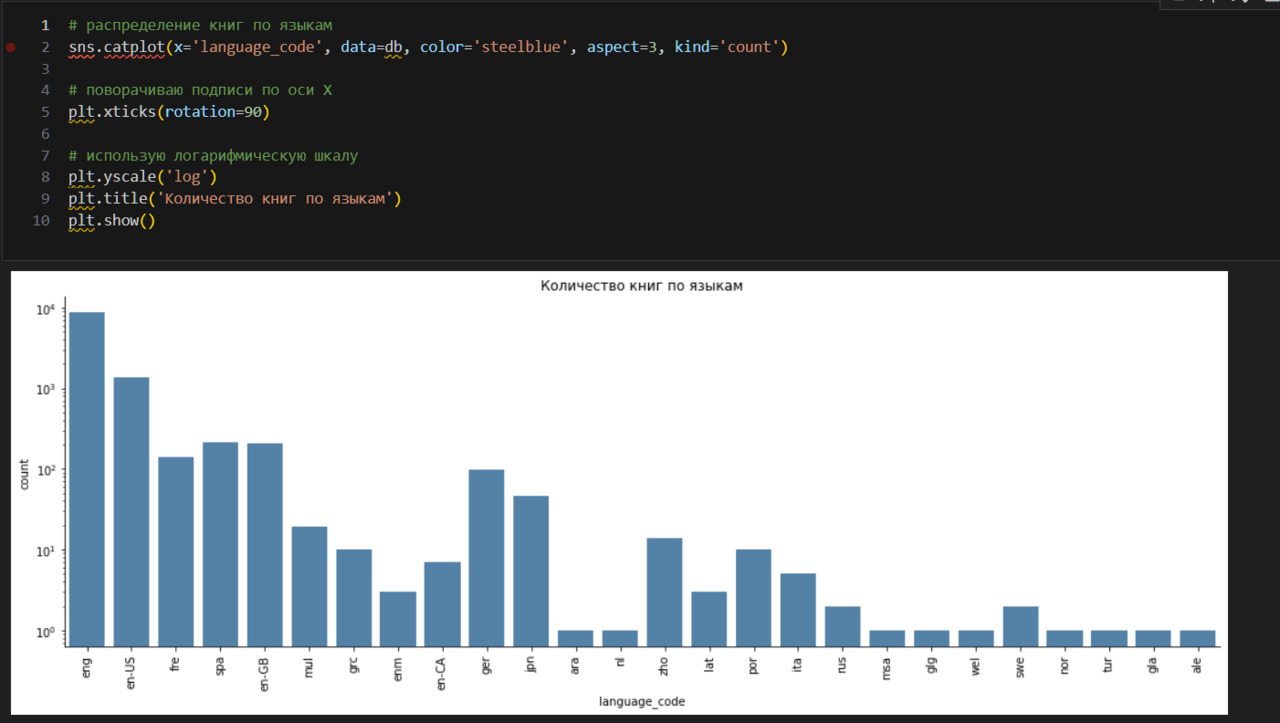
26 различных языков, самый частый eng, 8669.

Декад всего 13, самая частая — это 2000, на которую приходится 7332.

Кварталов 4, самый частый 3, на него приходится 2851 книга.

Категорий «с соавтором, переводчиком» и без две: либо переводчик или соавтор есть, либо их нет. Чаще всего их нет, таких случаев 6492.

Аналогично, либо книга является частью многотомного издания и тогда в колонке multivolume стоит 1, либо не является частью такого издания и тогда получается 0. Вижу, что в наборе, как правило, не многотомные издания (их 8147).

Опять-таки, а зачем мне эти знания? Во-первых, чтобы лучше понимать природу того объекта, который исследуется. В каком году книге чаще выходили? А в каком квартале? С каким названием? Все это может помочь понять не только, что выпускают издательства, но и вкусы читателей. Во-вторых, категориальные признаки позволяют разбить объекты на группы, скажем можно разбить книги по языку, и уже внутри каждой группы посмотреть оценки, количество страниц. Эта возможность ставит дополнительные задачи. Например, категории не должны быть слишком маленькими, так как невозможно будет доверять результатам. Например, если у меня по какому-то языку только две книги, то определить среднюю я смогу, но эта средняя может быть слишком далека от истинного значения. Надо помнить, что в статистике всегда руководствуются законом больших чисел.

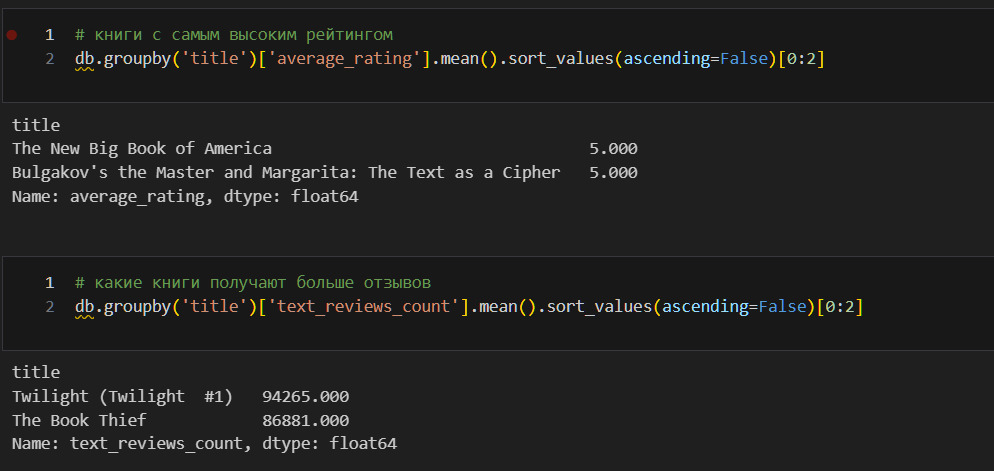
Ниже я приведу несколько способов агрегирования (группировки) данных.

Визуальный анализ

Визуальный анализ используют для того, чтобы «схватить» какие-то гипотезы на данных. Визуально человеку проще это сделать. Однако надо помнить, что размещение слишком большого количества данных на графике уменьшает этот эффект простоты. Например, на одном графике можно точками отразить распределение по двум признакам, сюда же добавить третий признак цветом точек, четвертый — размером точек, пятый — их формой. Но такой график будет крайне сложно прочитать, а значит и смысл в визуализации теряется.

Здесь я хочу установить следующее:

1) вид распределения целевого признака — средняя оценка;

2) наличие выбросов по количественным признакам;

3) наличие взаимосвязи между признаками;

4) соотношение категориальных данных там, где это уместно.

Ниже рассмотрю графики распределений.

В учебнике для инженеров выделяется четыре главных типа графиков:

1. график последовательного выполнения;

2. график задержки;

3. гистограмма;

4. график нормального распределения.

Подробнее прочитать о каждом типе графиков можно здесь (https://www.itl.nist.gov/div898/handbook/eda/section3/4plot.htm). Как выбрать необходимый тип графика можно понять из рисунка:

Ниже я рассмотрю только важные для моих задач графики.

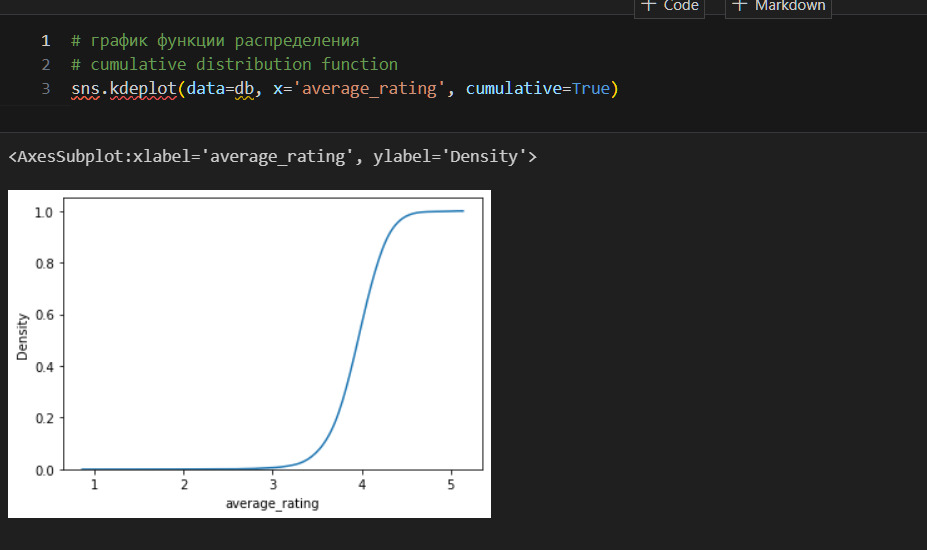
Сейчас я разберу, что такое функция распределения. Это имеет важное значение для понимания видов распределения и их смысла. Все начинается с функции распределения. Вот формальное определение:

«Функцией распределения называют функцию F (x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее x» (Гмурман, ст. 111).

А вот геометрический образ функции распределения:

«F (x) есть вероятность того, что случайная величина примет значение, которое изображается на числовой оси точкой, лежащей левее точки x» (Гмурман).

Выше показан график функции распределения. Как его правильно читать? Проведу из произвольной точки на оси x перпендикуляр. Точка пересечения перпендикуляра с графиком даст значение y — вероятность того, что моя произвольная точка примет значение равное или меньшее x. Например, беру оценку 4. Вижу, что вероятность получить такую оценку между 0,5 и 0,6, примерно 55%.

Раз у меня есть непрерывный график функции, я могу посчитать производные. Поэтому случайную величину можно представить и через т. н. плотность распределения (плотность вероятности).

«Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f (x) — первую производную от функции распределения F (x): f (x) = F» (x)» (Гмурман, стр. 116).

Пример такой функции ниже.

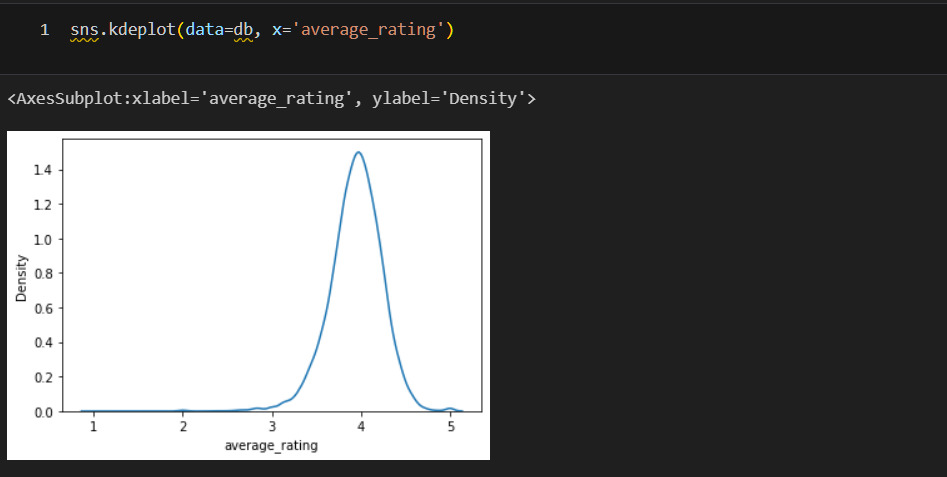
Законами распределения называют различные виды плотности распределения. Например, это может быть равномерное, нормальное, показательное распределение. Чаще всего используется нормальное распределение.

Про графики PDF, СDF, PPF подробнее здесь [1.3.6.2. Related Distributions] (https://www.itl.nist.gov/div898/handbook/eda/section3/eda362.htm)

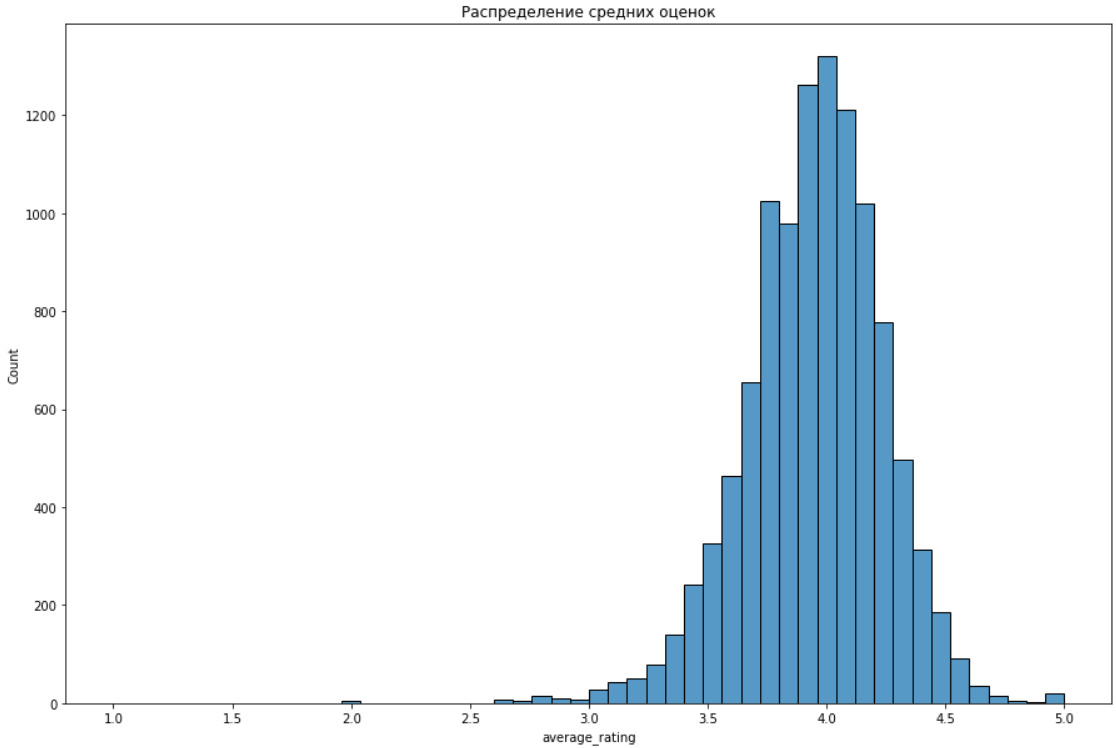
Гистограмма позволяет сделать предположение о виде распределения данных. Знать вид распределения данных необходимо по нескольким причинам. Во-первых, это позволяет делать предсказания о вероятности того или иного события. Во-вторых, для проведения статистических тестов, определения некоторых метрик требуется распределение определенного вида. Как правило, распределение должно быть нормальным. Если распределение нормальным не является, то данные можно привести к нормальному распределению или можно использовать специальные тесты, метрики. Поэтому важно ответить на вопрос: распределены ли данные нормально? Если нет, то нужно установить вид распределения.

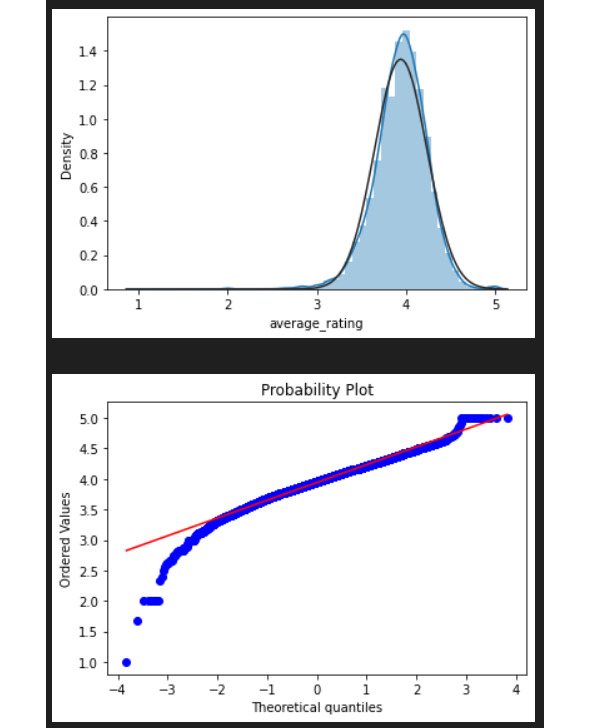
Гистограмма показывает, что средние оценки распределены практически нормально. Интересно, что в интервалах 2.5—3.0 и 4.8—5.0 видны небольшие подъемы линии. При нормальном распределении этого быть не должно. Это означает, что оценки в указанных интервалах имеют вероятность большую, чем это предсказывает нормальное распределение. Дополнительная проверка на нормальность распределения с помощью статистических методов будет показана ниже.

Гистограмму можно построить разными способами. В случае выше ширина столбика показывает частичный интервал, а высота — количество значений в этом интервале. Возможно построить гистограмму, где высота столбика будет показывать плотность. Подробнее см. в официальной документации функции (https://seaborn.pydata.org/generated/seaborn.histplot.html).

Про интерпретацию гистограммы можно также прочитать в [учебнике для инженеров] (https://www.itl.nist.gov/div898/handbook/eda/section3/histogra.htm). Там же можно обнаружить различные типы гистограмм (как нормальную, так и, например, бимодальную), а также дополнительные статистические методы для определения типа распределения в зависимости от типа гистограммы. Гистограмма показывает:

1) центральную характеристику данных;

2) масштаб данных;

3) скошенность;

4) наличие выбросов;

5) наличие нескольких мод в данных.

Трансформация данных к нормальному распределению объясняется в 6.5.2. What to do when data are non-normal (https://www.itl.nist.gov/div898/handbook/pmc/section5/pmc52.htm)

Выбросы

В учебнике для инженеров дано следующее определение выбросов:

«Выбросы — это точки данных, которые получены не из того же распределения, из которого получена основная масса данных».

То есть выброс — это такое значение, которое пришло не из того распределения, из которого пришли основные данные. В этом смысл того, чтобы определить распределение для большинства данных, а затем уже выброс. Редкие данные возможны и в границах распределения для основных данных, но вот выброс выходит вообще за границы распределения, то есть например за пределы колокола в нормальном распределении. В этом смысл того, что сначала надо найти отличающиеся от других данные, а затем проверить их на влиятельность.

Вот рекомендации по обработке выбросов из учебника для инженеров:

1. К каждому выбросу необходимо относиться серьезно. Не рекомендуется автоматически удалять выбросы. Наличие выбросов может быть не просто ошибкой в данных, выбросы могут сообщать важную информацию о данных. Поэтому надо постараться объяснить, чем вызваны выбросы в данных.

2. Если гистограмма показывает наличие выбросов, то рекомендуется следующее:

1) применить ящик с усами, который лучше гистограммы показывает наличие и количество выбросов;

2) применить Grubbs’ Test или иные тесты для обнаружения выбросов.

Рекомендуемые тесты на выбросы:

1) Grubbs’ Test — если тест на единичный выброс;

2) Tietjen-Moore Test — в случае, если в данных предполагается более одного выброса. Необходимо заранее знать точное количество выбросов.

3) Generalized Extreme Studentized Deviate (ESD) Test — также, если в данных более одного выброса. Необходимо знать только верхнюю границу ожидаемого числа выбросов. Рекомендуется, когда точное количество выбросов неизвестно.

Как правило, при обнаружении выбросов исходят из того, что данные распределены нормально. Если это не так, то можно привести данные к нормальному распределению.

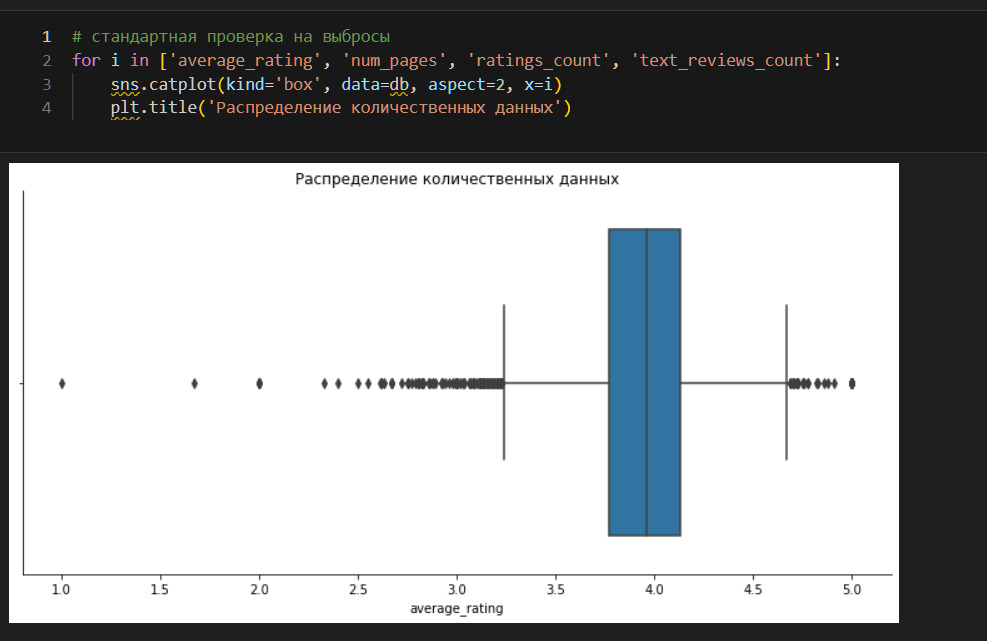
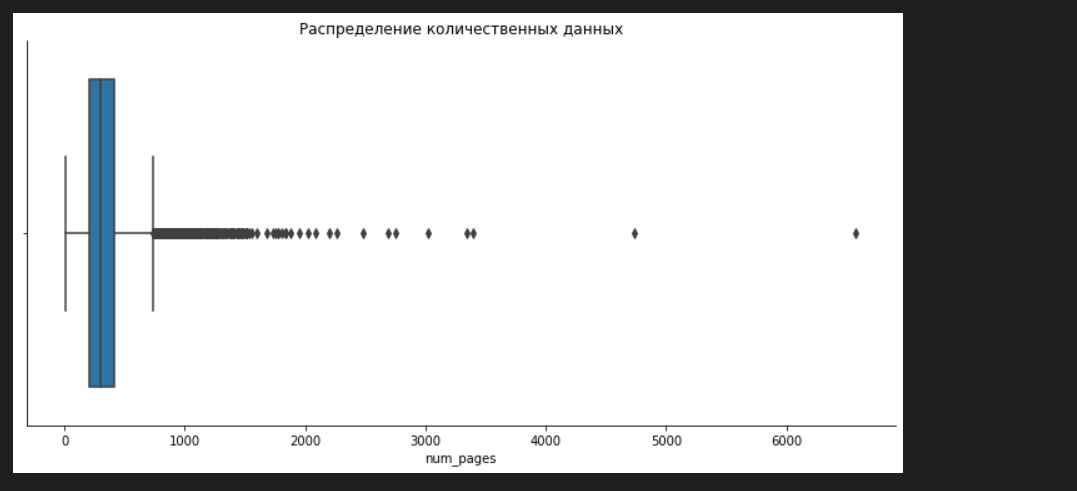
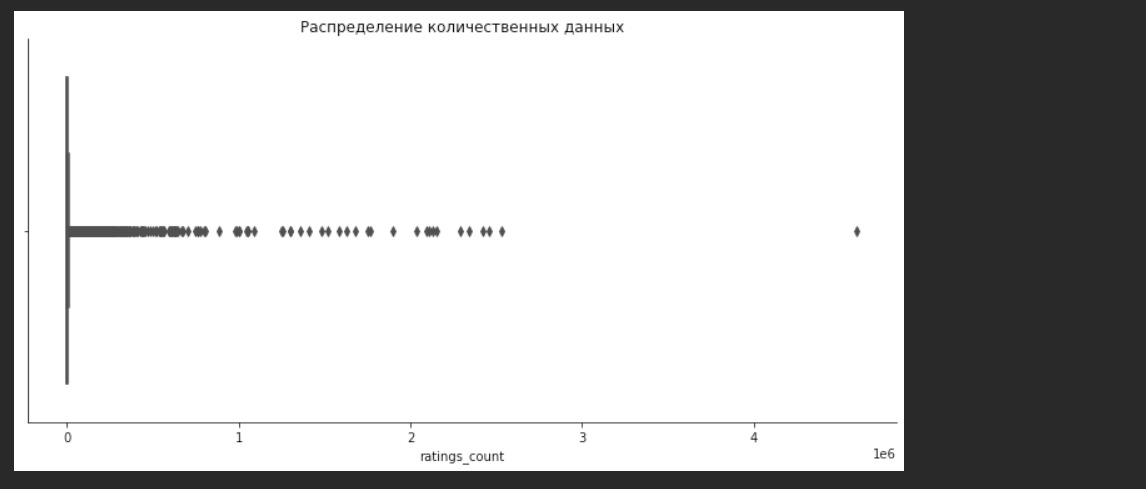
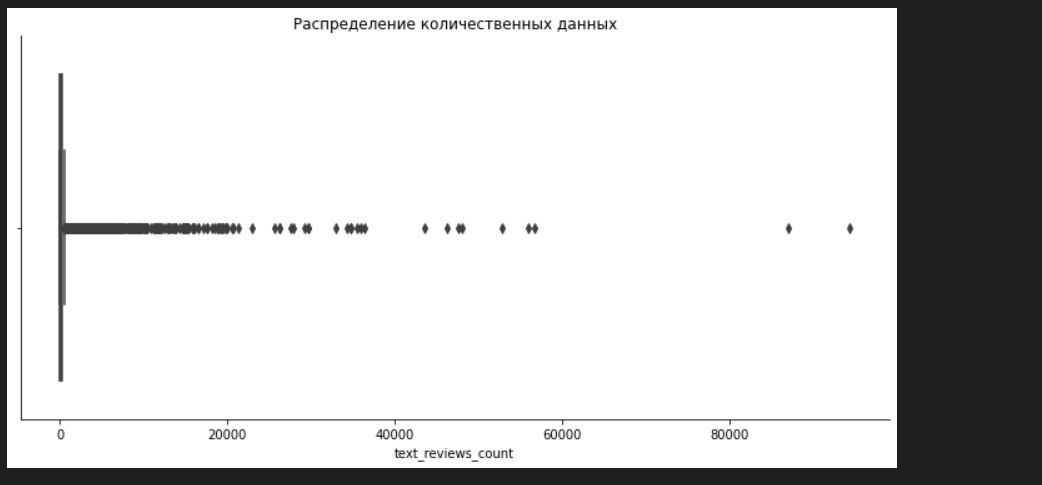
Это — ящики с усами. Их придумал отец-основатель анализа данных Тьюки. В середине прямоугольников показана медиана. Левый край прямоугольника — это 25%-квартиль, правый край — 75%. Усы — это межквартильный размах. За пределами усов — выбросы.

Интересный вопрос про ящик — это почему он то сжимается, то растягивается. Почему медиана скачет от левой стороны к правой? Ведь это медиана, она должна быть посередине. Все верно, почти. Разберу это на примере.

Важное терминологическое замечание.

«Квантиль 0,5 называют медианой. Для а = 0,25, 0,5 и 0,75 соответствующие квантили называются квартилями, а = 0,2, 0,4, 0,6, 0,8 они называются квинтилями».

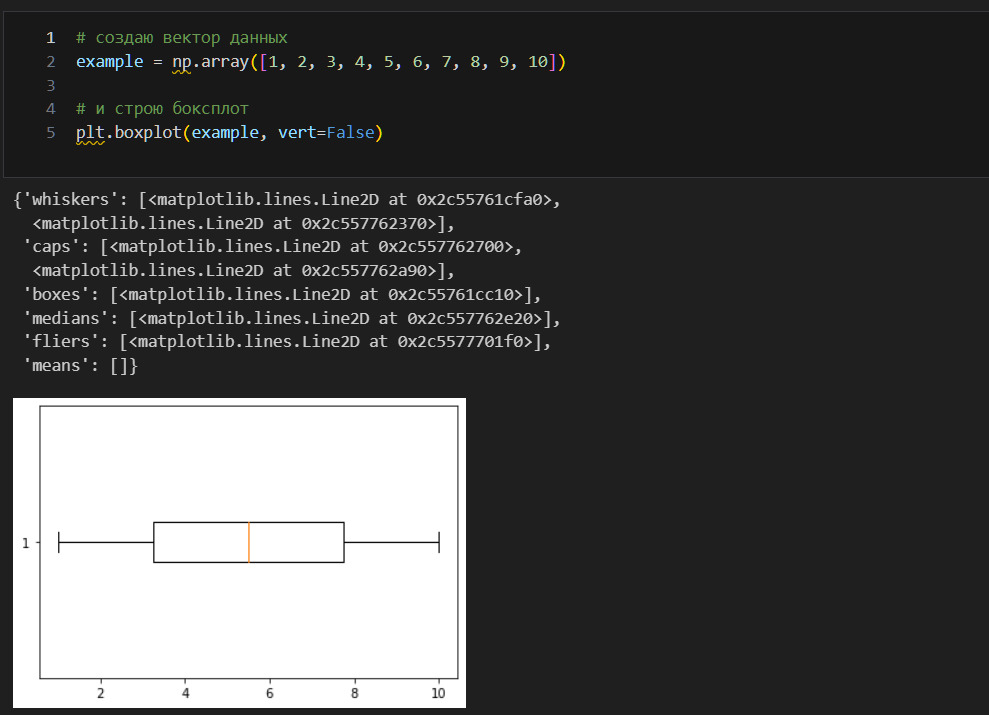
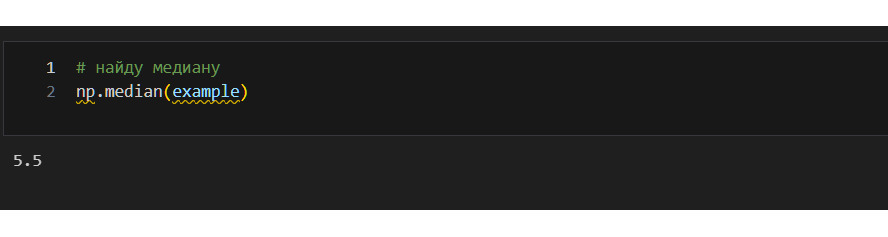
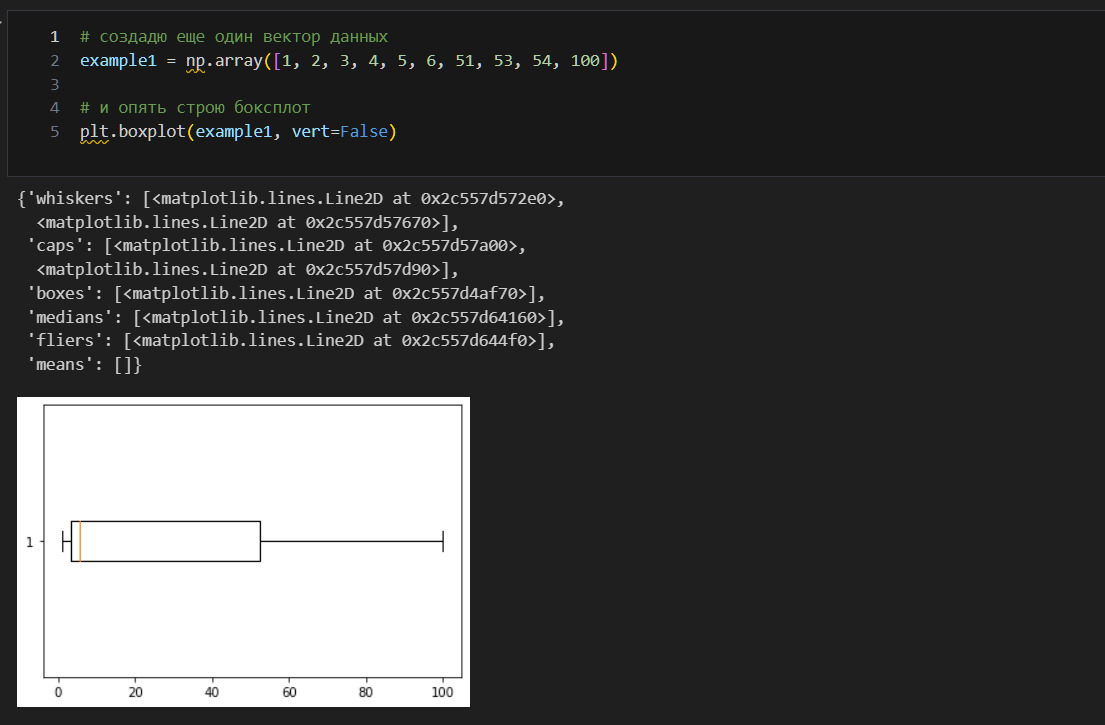
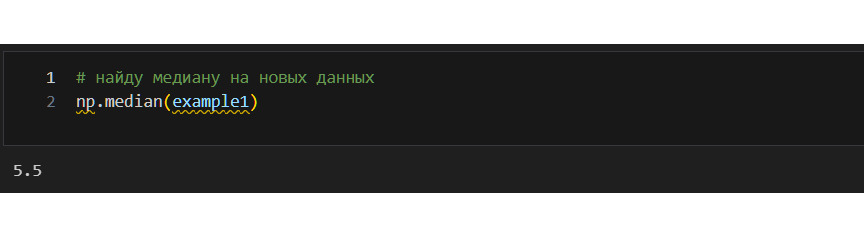
Что здесь произошло? Я создал второй вектор, где заменил 7, 8, 9, 10 на 51, 53, 54, 100. Количество значений не изменилось. Не изменилась и сама медиана — она осталась 5.5. Однако линия медианы «прижалась» к левой стороне ящика. Почему?

На оси x откладываются значения вектора. Ось y показывает количество таких значений. В первом случае на оси x отложены значения от 1 до 10. Во втором случае отложены значения от 1 до 100. Количество значений ниже и выше медианы не изменилось, но изменился масштаб.

Усы же строятся несколько иначе. Определяю границы усов (lower bound, upper bound). Смотрю, а какие из имеющихся значений не выходят за границы усов. До минимального (максимального) значения наших усов в установленных границах строю усы. Например, граница для верхнего уса 126, но фактически есть только значение 100. Строим ус до 100. Но граница нижнего уса — 71, однако минимальное фактическое значение это 1, поэтому строим ус до 1. Поэтому и возникает разница в длине усов.

Совет. Если я столкнулся с трудностью в понимании какой-либо формулы, статистики и т.п., то всегда начинаю с простого случая.

Итак, усы показывают число 3.23. Ниже этого числа — выбросы.

Визуализация категориальных данных

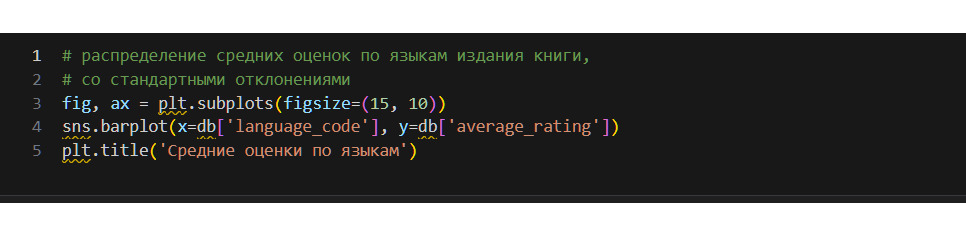
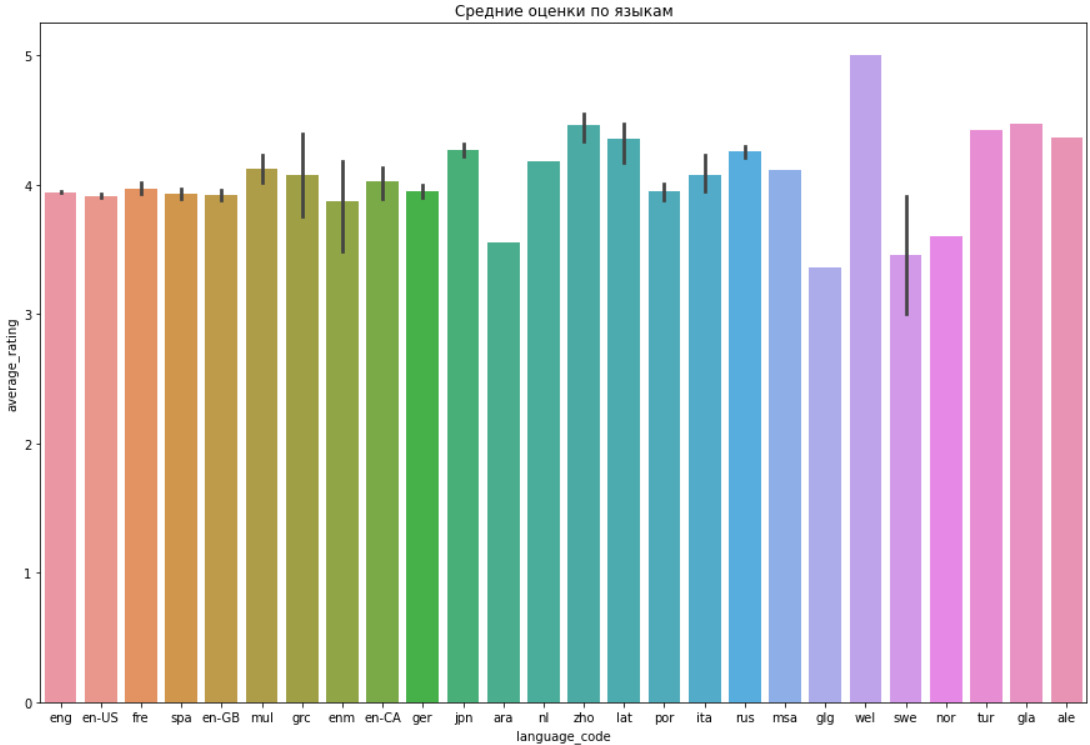
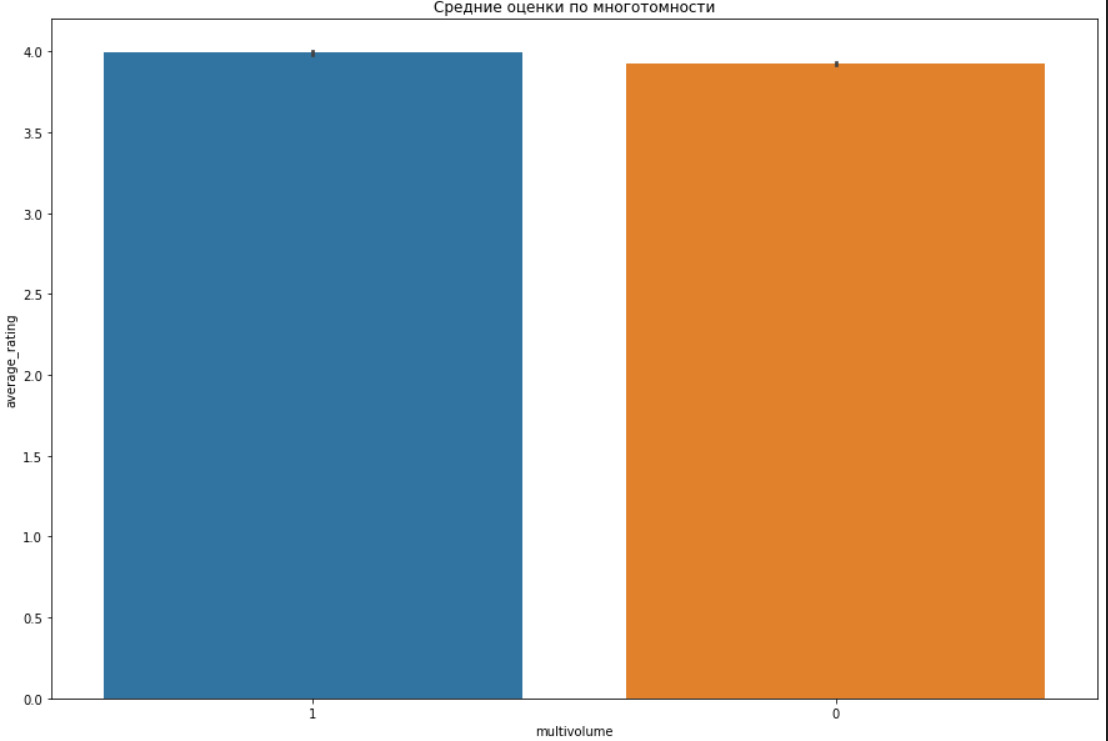
В последних графиках я использовал стандартное отклонение. Многие авторы рекомендуют всегда, когда это возможно, выводить графики именно с указанием стандартного отклонения. В самом деле, в рамках статистики простое указание на среднее значение недостаточно полно описывает данные, необходимо еще указать, как минимум, отклонение от среднего.

Проверка статистических гипотез

Проверка статистических гипотез является важной задачей математической статистики. Вот цитата из Гмурмана, которая должна это показать.

«Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.

Например, статистическими являются гипотезы:

1) генеральная совокупность распределена по закону Пуассона;

2) дисперсии двух нормальных совокупностей равны между собой.

В первой гипотезе сделано предположение о виде неизвестного распределения, во второй — о параметрах двух известных распределений» (Гмурман, стр. 281).

Гипотезы делят на нулевую (основную) и конкурирующую (альтернативную). Если можно принять нулевую гипотезу, то необходимо отвергнуть альтернативную. Если же принять нулевую гипотезу нельзя, то необходимо принять альтернативную. Пример: если нулевая гипотеза утверждает, что математическое ожидание равно 10, то альтернативная гипотеза будет утверждать, что математическое значение не равно 10.

Нулевая гипотеза может быть либо истинной, либо ложной. Независимо от этого, можно угадать истинность или угадать ложность гипотезы, или не угадать ни того, ни другого. С учетом этого, возможные ошибки делят на два вида:

1) ошибка первого рода возникает, если отвергнута истинная гипотеза. Например, если гипотеза, что математическое ожидание равно 10, является истинной, но пришлось ее отвергнуть, то возникает ошибка первого рода;

2) ошибка второго рода возникает, если принята неправильная гипотеза. Например, если гипотеза, что математическое ожидание равно 10, является ложной, но пришлось ее принять, то возникает ошибка второго рода.

«Вероятность совершить ошибку первого рода принято обозначать через a; ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости, равный 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода (отвергнуть правильную гипотезу)» (Гмурман, стр. 283).

Итак, есть нулевая гипотеза. Возникает вопрос, а как ее проверить? То есть как узнать, что это гипотеза истинная, или узнать, что гипотеза ложная?

Чтобы проверить нулевую гипотезу, нужно выплонить несколько шагов:

1) подобрать специальную случайную величину, распределение которой точно или примерно известно. Эта величина может быть обозначена как U или Z при нормальном распределении, F — при распределении Фишера-Снедекора и т. п. Эту величину называют статистическим критерием;

2) на основании имеющихся данных рассчитать те значения, которые входят в специальную случайную величину. Так получают частное (наблюдаемое) значение критерия.

Вот это на примере. Предположим, что специальная случайная величина это F = s1**2 / s2**2 (Гмурман, стр. 283). Тогда можно посчитать на наборе данных показатели s1 и s2, а значит расчитать F. Что дальше?

«После выбора определенного критерия множество всех его возможных значений разбиваются на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другая — при которых она принимается.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.

Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия принадлежит критической области — гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы — гипотезу принимают.

Поскольку критерий K — одномерная случайная величина, все ее возможные значения принадлежать некоторому интервалу. Поэтому критическая область и область принятия гипотезы также являются интервалами и, следовательно, существуют точки, которые их разделяют.

Критическими точками (границами) k (кр) называют точки, отделяющие критическую область от области принятия гипотезы.

Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области.

Правосторонней называют критическую область, определяемую неравенством K> k (кр), где k (кр) — положительное число.

Левосторонней называют критическую область, определяемую неравенством K <k (кр), где k (кр) — отрицательное число.

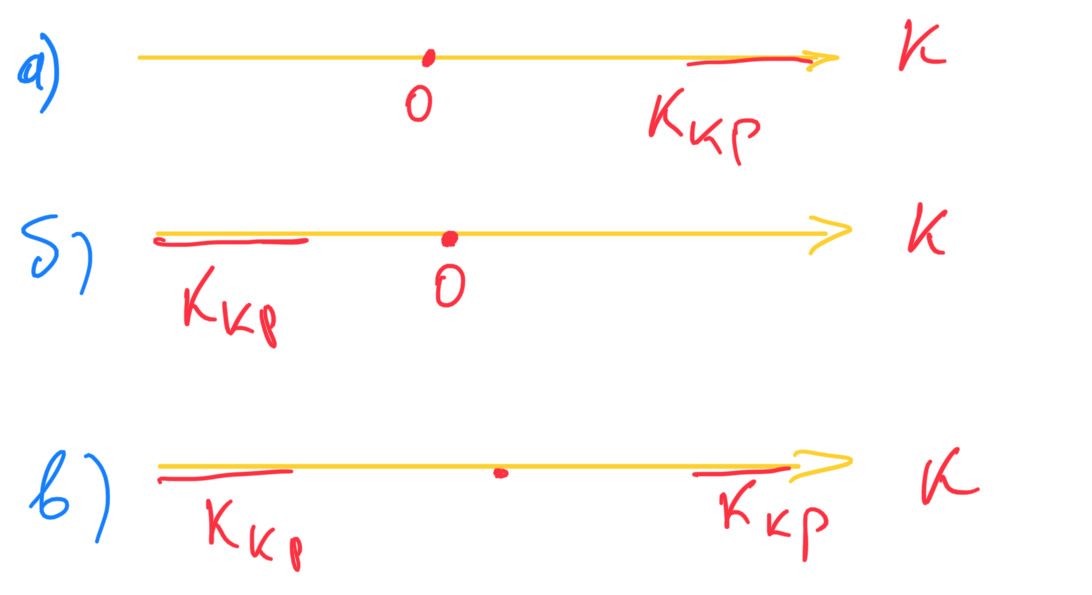
Односторонней называют правостороннюю или левостороннюю критическую область.

Двусторонней называют критическую область, определяемую неравенствами K <k (кр) 1, K> k (кр) 2, где k (кр) 2> k (кр) 1» (Гмурман, ст. 284)

Как найт критическую точку? Для этого выбирают небольшой уровень значимости a.

«Затем ищут критическую точку, исходя из требования, чтобы при условии справедливости нулевой гипотезы вероятность того, что критерий К примет значения, большее k (кр) была равна принятому уровню значимости:

P (K> k (кр)) = а».

Это значение P также называют p-value.

Важно также помнить, что проверка статистических гипотез не доказывает гипотезы. Одного доказательства еще не достаточно для принятия гипотезы. Однако достаточно одного противоречащего гипотезе факта, чтобы ее отвергнуть. Поэтому проверяют гипотезу на возможность принятия несколькими способами, а для отрицания гипотезы хватит и одного.

Еще одна важная концепция — это мощность критерия.

«Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза. Другими словами, мощность критерия есть вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза» (Гмурман, стр. 287).

В гл. 19 Гмурмана можно найти много примеров на расчет статистик и проверку гипотез.

Вот пример того же самого, но на основе t-testa. Для такой статистики как t-критерий нулевая гипотеза — это равенство средних значений двух выборок. Альтернативная гипотеза: средние двух выборок не равны. P-value это вероятность получить равенство средних значений на тех выборках, что у нас есть. Если такая вероятность меньше заданного уровня (как правило, 0.05), то надо отвергнуть нулевую гипотезу. Другими словами, если p-value <0.05, то вероятность получить равенство двух средних значений очень низкая. Вероятность представляется значениями от 0 до 1, где 0 — это невозможное событие, 1 — это событие, которое безусловно произойдет. Из этого видно, что 0.05 это очень близкое значение к 0, то есть невозможности. Поэтому надо отбросить нулевую гипотезу и принять альтернативную: средние двух выборок не равны.

Дополнительно надо учитывать, что тесты могут быть параметрическими и непараметрическими. Параметрические тесты основаны на известных свойствах распределений. Непараметрические не учитывают свойства распределений. В случае непараметрических тестов метрики распределения определяются с помощью многократного повторения теста.

Также все тесты можно разделить на: применимые только к количественным признакам, применимые только к категориальным признакам, применимые как к количественным, так и категориальным признакам.

Еще одно деление: одни тесты говорят только о наличии связи (отсутствии связи) между признаками, другие тесты также показывают силу этой связи.

Дополнительно про статистические тесты см. главу 7.1.Introduction (https://www.itl.nist.gov/div898/handbook/prc/section1/prc1.htm).

Проверка на нормальное распределение

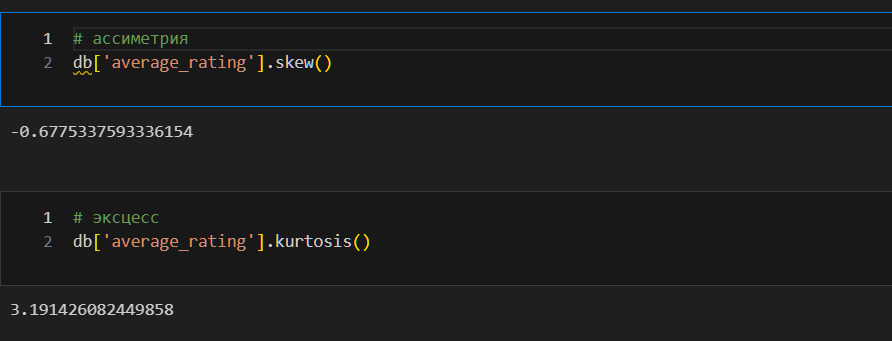
Базовая проверка на нормальное распределение может быть проведена с помощью критериев ассиметрии и эксцесса. Выше я уже дал теоретическое описание данных критериев.

Теперь практические правила интерпретации.

1. «Если „длинная часть“ кривой расположена правее моды (точки максимума дифференциальной функции), то ассиметрия положительная, если слева — отрицательна» (Гмурман, стр. 138).

2. «Если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и „острую“ вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и „плоскую“ вершину, чем нормальная кривая» (там же).

3. Если skew положителен, то данные скошены вправо, а если отрицателен то влево. Если kurtosis (эксцесс) положительный, то распределение имеет острую вершину, если отрицательный, то распределение имеет пологую вершину. Нормальное распределение имеет скошенность 0 и вершину около 4. Эксцесс — это статистическая мера, которая определяет, насколько сильно хвосты распределения отличаются от хвостов нормального распределения. Другими словами, эксцесс определяет, содержат ли хвосты данного распределения экстремальные значения.

Здесь я использую Normal Probability Plot. Подробнее про этот график можно прочитать здесь (https://www.itl.nist.gov/div898/handbook/eda/section3/normprpl.htm). Хорошее объяснение и пример построения графика можно найти также здесь (https://www.storyofmathematics.com/normal-probability-plot).

Вот как выглядит график в общем виде:

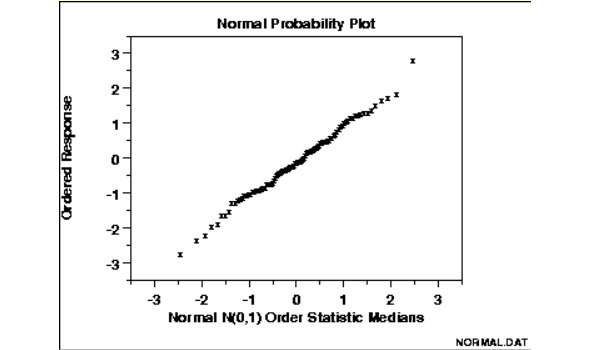
По вертикали графика откладываем упорядоченные данные. По горизонтали откладываем Normal order statistic medians.

Как считается вот этот Normal order statistic medians? Это можно обнаружить по ссылке выше.

Normal Probability Plot отвечает на вопросы:

1) данные распределены нормально?

2) какой природы распределение? есть скос? хвост длинный или короткий?

Как и для большинства иных тестов, для этого графика важно соблюдение требования о случайности данных.

Здесь можно применить технику приближенного понимания. То, о чем говорит график Normal Probability Plot, это по существу наложение гистограммы по имеющимся данным на гистограмму, о которой известно, что она соответствует нормальному распределению.

Теперь про интерпретацию. Главная интерпретация в том, что график должен быть линейным, чтобы можно было говорить о том, что применимо нормальное распределение. Важно, что линия строится между точкой первого и третьего квартиля. Про отклонения от прямой читайте здесь и ниже (https://www.itl.nist.gov/div898/handbook/eda/section3/eda33l2.html).

Для определения типа распределения можно использовать Tukey Lambda PPCC. На Python его можно найти здесь (https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ppcc_plot.html). В этом случае распределение определяется по значению лямбды. Еще здесь 1.3.6.6.15. Tukey-Lambda Distribution (https://www.itl.nist.gov/div898/handbook/eda/section3/eda366f.htm).

График Quantile-Quantile Plot отвечает на вопрос «происходят ли два набора данных из одного распределения». В этом смысле график Normal Probability Plot есть только частный случай графика Quantile-Quantile Plot. Подробнее про этот последний здесь (https://www.itl.nist.gov/div898/handbook/eda/section3/qqplot.htm), а также здесь pg. qqplot (https://pingouin-stats.org/generated/pingouin.qqplot.html#pingouin.qqplot)

Ниже я применю тест Шапиро. См. подробнее здесь (https://pingouin-stats.org/generated/pingouin.normality.html?highlight=shapiro)

На этом примере еще раз разберу, что же означает применение статанализа. Я вычисляю интересующую меня статистику (в данном случае — Шапиро) и проверяю нулевую гипотезу. Например, здесь нулевая гипотеза: данные распределены нормально. Так как p-value <0.05 (так как вывод имеет экспоненциальную форму «e-40»), я должен отвергнуть нулевую гипотезу и принять альтернативную, то есть отвергаю гипотезу, что данные распределены нормально, и принимаю гипотезу, что данные не распределены нормально. Такой результат называется статистически значимым. Возможно применение и иных методов: тест на нормальность D’Agostino-Pearson, тест Колмогорова-Смирнова.

Итак, данные не распределены нормально. В это случае можно применить непараметрические тесты, например, корреляцию Спирмена или перестановочный тест (пермутацию).

Совет. Если предположения о нормальности или однородности дисперсий не выполняются, то можно преобразовать данные таким образом, чтобы они соответствовали нормальным. В этом случае важно помнить, что интерпретация результатов теста требует выполнения обратных преобразований данных. Некоторые преобразования данных по-разному влияют на нормальность и дисперсию, поэтому следует проверять различные преобразования. Есть, конечно, общие преобразования, которые используются. О них я расскажу ниже.

Корреляция

Стандартный тест для количественных признаков — это проверка корреляции Пирсона. Однако предварительно надо проверить условия для этого теста. Если условия соблюдаются, то можно применять тест. Если условия не соблюдаются, то можно либо подогнать данные к нормальному распределению, либо использовать непараметрические тесты. Это правило применяется к любому тесту: всегда надо сначала проверить соблюдение условий для применения конкретного теста.

Когда применяется?

Корреляция по Пирсону применяется, когда нужно проверить связь между двумя непрерывными переменными.

Условия применения теста

1) независимость выборок,

2) нормальное распределение.

Альтернативы, если условия не выполняются

Непараметрические тесты, корреляция Спирмена, пермутация

Формула

См. подробнее здесь (https://www.pythonfordatascience.org/variance-covariance-correlation/)

Интерпретация

Если значение больше 0 и меньше 1, то положительная корреляция (уменьшение-уменьшение (минус на минус дает плюс), увеличение-увеличение (плюс на плюс дает плюс)), при 0 связи нет, если меньше 0, то отрицательная (уменьшение-увеличение (минус на плюс дает минус), увеличение-уменьшение (плюс на минус дает минус)).

Особенности

Важно, если связь носит нелинейный характер, тогда возможна ошибочная интерпретация. Чувствителен к выбросам, можно применять робастную корреляцию Пирсона.

Если есть подозрение, что третья переменная влияет на две, у которых смотрим корреляцию, то можно применить частичную корреляцию.

Можно использовать Distance correlation для определения не только линейной, но и нелинейной связи переменных.

Сильно коррелированные переменные можно объединить в одну, например через умножение, деление. Удалять изначальные нельзя. Можно также использовать метод главных компонент. При подозрении на нелинейность связи возможно применение регуляризации, например Lasso или Ridge.

Независимость выборок понятие оценочное, поэтому определяется исследователем. Нормальное распределение можно проверить специальными методами: визуально, тестами.

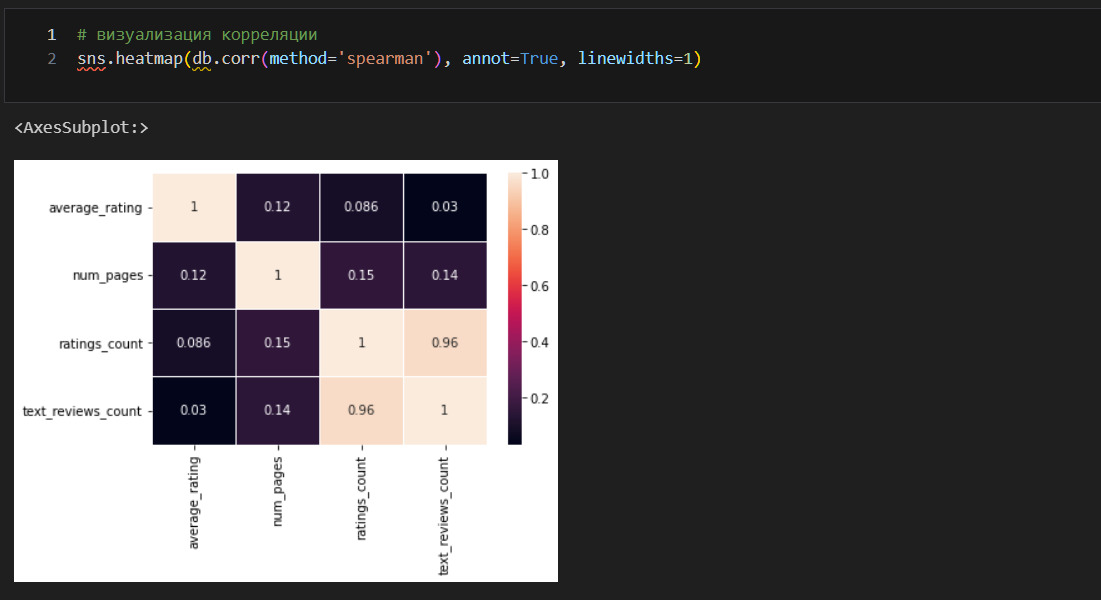
Получилась таблица корреляции «один против всех», когда один признак average_rating проверяется на корреляцию со всеми остальными. Разберу, что означает каждый показатель.

n — это количество наблюдений (строк), которые учитывались при построении корреляции;

r — это коэффициент корреляции по Спирмену. Хорошее объяснение можно найти в книге «Статистика для всех» Сары Бослаф. Видно, что корреляция слабая. Возможно только, что количество страниц связано положительной корреляцией с оценкой, то есть уменьшение количества страниц ведет к уменьшению оценки, увеличение — к увеличению;

CI95% — это доверительный интервал для r. Важно помнить, что во всех случаях, когда это позволяют статистические тесты, результаты таких тестов необходимо приводить с доверительными интервалами;

r2 — это коэффициент детерминации, то есть какая доля дисперсии average_rating может быть объяснена другим признаком;

z — это стандартизированная оценка корреляции;

p-unc — это не скорректированная оценка p-value;

p-corr — это скорректированная оценка p-value;

p-adjust это поправка, которую применили к p-value. В данном случае Бонферрони;

power это мощность, то есть 1 минус вероятность допустить ошибку 2 типа. Другими словами, вероятность обнаружения существующей закономерности.

Выводы

Получил корреляцию между average_rating и числовыми признаками. Вывод следующий: средняя оценка не имеет значимых связей с другими количественными данными. Кажется, что не достигнуто никакого результата? Это не так. Во-первых, отсутствие сильной корреляции пригодится при машинном обучении. Во-вторых, установлено, например, что от количества страниц в книге оценка не зависит. В то же время зависимость от количества страниц все же выше, чем от количества оценок или количества обзоров. Другими словами, желание читателей оставить отзыв не коррелирует с оценкой.

Остается вопрос, а как быть с категориальными признакми? Здесь понадобится дисперсионный анализ. Но сначала визуализирую корреляцию.

Дисперсионный анализ

Здесь я дам сначала описание дисперсионного анализа по Гмурману (стр. 349 и далее).

«На практике дисперсионный анализ применяют, чтобы установить, оказывает ли существенное влияние некоторый качественный фактор F, который имеет p уровней F1, F2, F3… Fp, на изучаемую величину X. Например, если требуется выяснить, какой вид удобрений наиболее эффективен для получения наибольшего урожая, то фактор F — удобрение, а его уровни — виды удобрений.

Основная идея дисперсионного анализа состоит в сравнении «факторной дисперсии», порождаемой воздействием фактора, и «остаточной дисперсии», обусловленной случайными причинами. Если различие между этими дисперсиями значимо, то фактор оказывает существенное влияние на X: в этом случае средние наблюдаемых значений на каждом уровне (групповые средние) различаются также значимо.

Если уже установлено, что фактор существенно влияет на X, а требуется выяснить, какой из уровней оказывает наибольшее воздействие, то дополнительно производят попарное сравнение средних.

Иногда дисперсионный анализ применяется, чтобы установить однородность нескольких совокупностей (дисперсии этих совокупностей одинаковы по предположению; если дисперсионный анализ покажет, что и математические ожидания одинаковы, то в этом смысле совокупности однородны). Однородные же совокупности можно объединить в одну и тем самым получить о ней более полную информацию, следовательно, и более надежные выводы.

В более сложных случаях исследуют воздействие нескольких факторов на нескольких постоянных или случайных уровнях и выясняют влияние отдельных уровней и их комбинаций (многофакторный анализ)».

Теперь о том, как это считается.

Итак, вот какие предположения:

1) есть количественный нормально распределенный признак X;

2) на этот признак воздействует фактор F;

3) фактор F имеет p постоянных уровней;

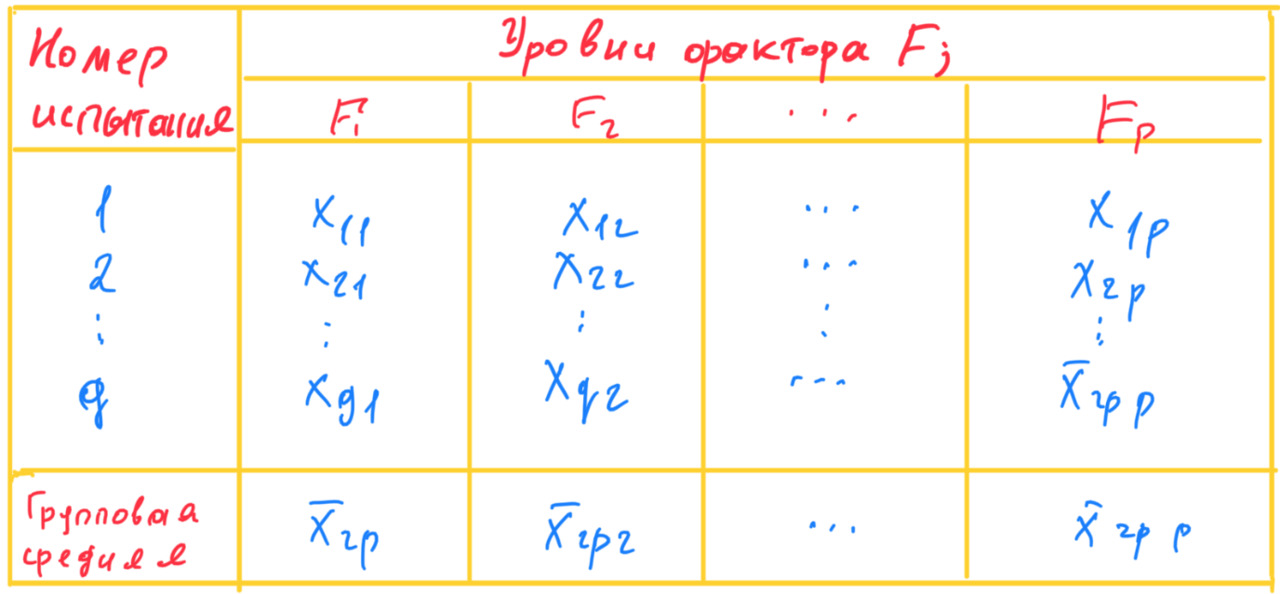
4) число наблюдений (испытаний) на каждом уровне одинаково и равно q (это не обязательно должно быть так, см. стр. 358 Гмурмана).

Всего наблюдений n=pq значений x (ij) признака X, где i — номер испытания (i = 1, 2,…q), j — номер уровня фактора (j = 1, 2, …p). Вот как это выглядит в таблице.

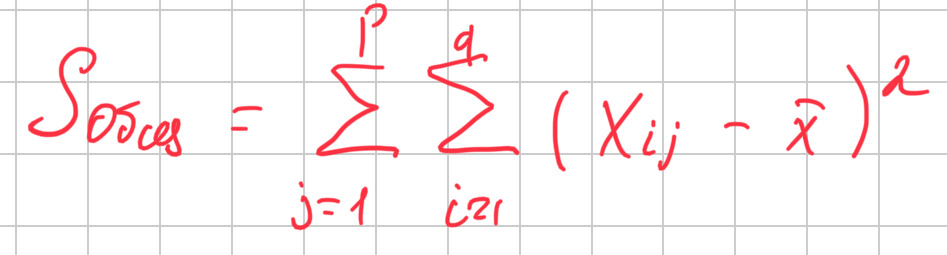
Теперь введу показатель Sобщ — общая сумма квадратов отклонений наблюдаемых значений от общей средней.

Следующий показатель S (факт) — это факторная сумма квадратов отклонений групповых средних от общей средней, которая характеризует «рассеяние между группами».

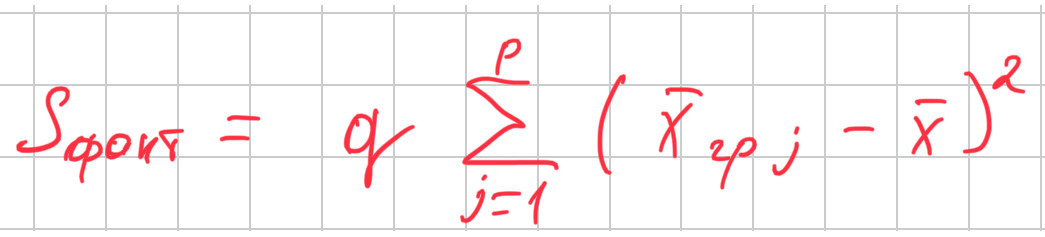
Еще один показатель S (ост) — остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней, которая характеризует рассенияние «внутри группы».

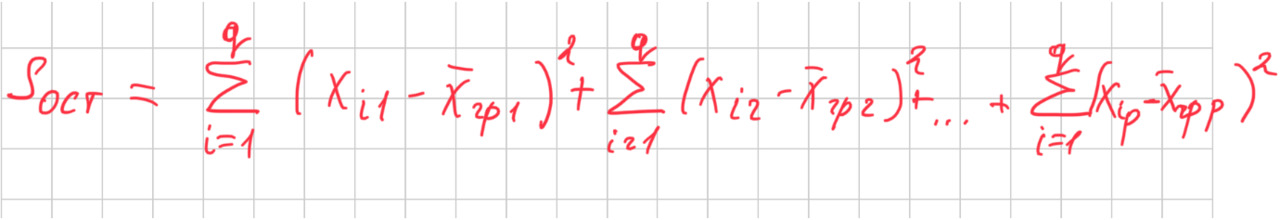
Остаточную сумму можно определить и проще:

Понять это можно примерно так как на графике

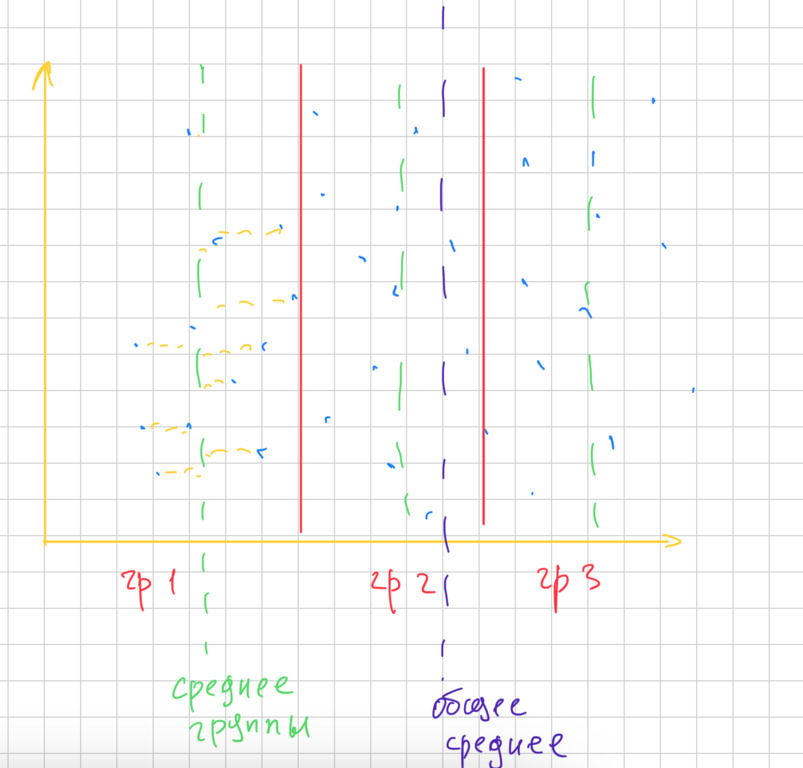
Как прочитать этот график? Есть группы, которые разделены красными вертикальными чертами. Для каждой группы определено среднее — зеленая линия. Но есть также общая для всех точек средняя — фиолетовая черта. Для первой группы горизонтальной желтой штриховкой показано, что значит разность между средним и значением. Есть также разность среднего группового и общего среднего.

Хорошее пояснение этих показателей дано на стр. 352 Гмурмана. Привожу его целиком:

«1. Убедимся, что S (факт) характеризует воздействие фактора F. Допустим, что фактор оказывает существенное влияние на X. Тогда группа наблюдаемых значений признака на одном определенном уровне, вообще говоря, отличается от групп наблюдений на других уровнях. Следовательно, различаются и групповые средние, причем они тем больше рассеяны вокруг общей средней, чем большим окажется воздействие фактора. Отсюда следует, что для оценки воздействия фактора целесообразно составить сумму квадратов отклонений групповых средних от общей средней (отклонение возводят в квадрат, чтобы исключить погашение положительных и отрицательных отклонений). Умножив эту сумму на q, получим S (факт). Итак, S (факт) характеризует воздействие фактора.

2. Убедимся, что S (ост) отражает влияние случайных причин. Казалось бы, наблюдения одной группы не должны различаться. Однако, поскольку на X, кроме фактора F, воздействуют и случайные причины, наблюдения одной и той же группы, вообще говоря, различны и, значит, рассеяны вокруг своей групповой средней. Отсюда следует, что для оценки влияния случайных причин целесообразно составить сумму квадратов отклонений наблюдаемых значений каждой группы от своей групповой средней, то есть S (ост). Итак, S (ост) характеризует воздействие случайных причин.

3. Убедимся, что S (общ) отражает влияние и фактора, и случайных причин. Будем рассматривать все наблюдения как единую совокупность. Наблюдаемые значения признака различны вследствие воздействия фактора и случайных причин. Для оценки этого воздействия целесообразно составить сумму квадратов отклонений наблюдаемых значений от общей средней, то есть S (общ)».

Вот пример. Предположим, надо проверить при заданном уровне значимости нулевую гипотезу о равенстве нескольких средних нормальных совокупностей с неизвестными, но одинаковыми дисперсиями.

«Для того чтобы проверить нулевую гипотезу о равенстве групповых средних нормальных совокупностей с одинаковыми дисперсиями, достаточно проверить по критерию F [отношение квадрата большей дисперсии к квадрату меньшей дисперсии, распределение Фишера-Снедекора] нулевую гипотезу о равенстве факторной и остаточной дисперсий. В этом и состоит метод дисперсионного анализа».

(Гмурман, стр. 356)

Для моего исследования важно проверить следующие предположения:

1) на среднюю оценку влияет наличие или отсутствие соавтора/переводчика;

2) на среднюю оценку влияет декада;

3) на среднюю оценку влияет квартал, в котором издана книга;

4) на среднюю оценку влияет многотомность издания.

Дам более формальное описание дисперсионного анализа, который также называют ANOVA.

Общие условия применения теста ANOVA

1) выборки независимые;

2) зависимая переменная нормально распределена;

3) соблюдается равенство дисперсий. Раньше я выяснил, что данные не распределены нормально. Ниже проверю еще равенство дисперсий.

Дисперсионный анализ однофакторный

Когда применяется

Проверка средних значений определенной переменной в двух и более группах. Смысл теста таков. Тест проверяет общую разницу между переменными в модели, то есть, что по крайней мере одна из групп статистически значимо отличается от других. Однако, если ANOVA значима, нельзя сказать, какие группы отличаются. Чтобы определить, какие группы отличаются друг от друга, необходимо провести плановые или послеплановые сравнения. Например, можно применить апостериорный тест Шеффа для отбора групп.

Условия применения теста

1) зависимая переменная — непрерывная, факторы — дихотомические или категориальные. Если некоторые переменные являются категориальными, а другие непрерывными, то анализ называется анализом ковариации (ANCOVA, см. ниже);

2) каждое значение зависимой переменной не должно зависеть от других ее значений;

3) нормальное распределение зависимой переменной. Для данного теста предположение о нормальности распределения проверяется на остатках;

4) однородность дисперсии.

Альтернативы, если условия не выполняются

Непараметрический тест Краскела-Уоллиса

Формула

См. подробнее здесь (https://www.pythonfordatascience.org/anova-python/)

Интерпретация

См. подробнее здесь (https://www.pythonfordatascience.org/anova-python/)

Особенности

При проведении ANOVA с несколькими факторами, как в рассматриваемом случае, все факторы должны быть проверены на взаимодействие, прежде чем рассматривать их индивидуальные основные эффекты. Если взаимодействие между переменными несущественно, то надо удалить переменные из взаимодействия и провести анализ снова.

Дисперсионный анализ. Многофакторный

Когда применяется?

Если есть 2 и более фактора.

Условия применения теста

Как в однофакторном

Особенности

Нулевая гипотеза: нет разницы для зависимой переменной от фактора (взаимодействия факторов)

ANCOVA

Когда применяется?

Если один из факторов — непрерывная переменная.

Условия применения теста

Как обычная ANOVA плюс:

1) независимость ковариант и эффектов фактора. Проверяется по ANOVA;

2) однородность регрессионных наклонов. Определяется по графику.

Проверка равенства дисперсий может быть осуществлена с помощью:

1) теста Барлетта. Чувствителен к отклонению данных от нормального распределения, поэтому при наличии таких отклонений применяется с осторожностью;

2) тест Левена. Менее чувствителен к отклонениям данных от нормального распределения.

Если условие по дисперсии не выполняется то можно:

1) применить непараметрический тест, например t-тест Вэлча;

2) изменить данные.

Ссылки на дополнительные материалы:

ANOVA здесь [1.3.5.4. One-Factor ANOVA] (https://www.itl.nist.gov/div898/handbook/eda/section3/eda354.htm) и далее. И еще здесь и далее [3.2.3. Analysis of Variance Models (ANOVA)] (https://www.itl.nist.gov/div898/handbook/ppc/section2/ppc23.htm)

Тест Бартлетта на равнество дисперсий здесь 1.3.5.7. Bartlett’s Test (https://www.itl.nist.gov/div898/handbook/eda/section3/eda357.htm). Дальше идет хи-квадрат, F-тест, тест Левена, измерение скошенности и эксцесса, автокорреляция, тест Андерсона-Дарлинга, тест Колмогорова-Смирнова.

Еще про ANOVA здесь и далее 7.4.2. Assuming the observations are normal, do the processes have the same variance? (https://www.itl.nist.gov/div898/handbook/prc/section4/prc42.htm)

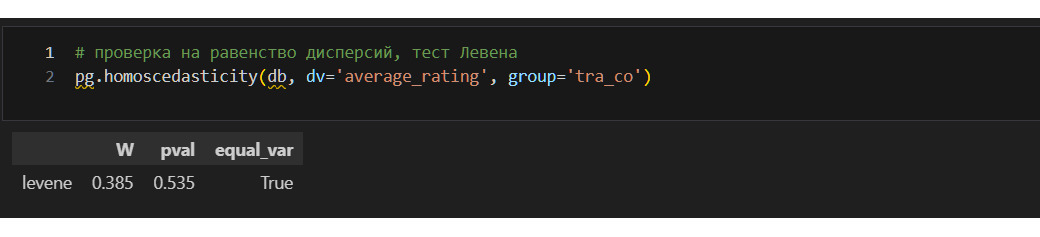
Если в тесте Левина p-value> 0.05, то не отвергаю нулевую гипотезу: дисперсии равны. Принимаю нулевую гипотезу о равенстве дисперсий, так как p-value> 0.05. Однако данные распределены не нормально, поэтому применить параметрический тест нельзя. Нужна непараметрическая проверка. Воспользуюсь, например, перестановочным тестом.

Смысл перестановочного теста в следующем. Надо посчитать различаются ли средние между группами в признаке. Считаю эту разницу на фактических данных. Далее перемешиваю данные по группам, выделяю из этих данных новые две группы, считаю статистику на них. Так делаю, например, 10000 раз. Получаю 10000 значений статистики. Смотрю, сколько раз в этом списке полученных значений встречалось наше изначальное значение. Вычисляю вероятность. Если p-value было меньше 0.05, то это означает, что случайно получить разницу средних маловероятно, а значит эта разница носит не случайный характер.

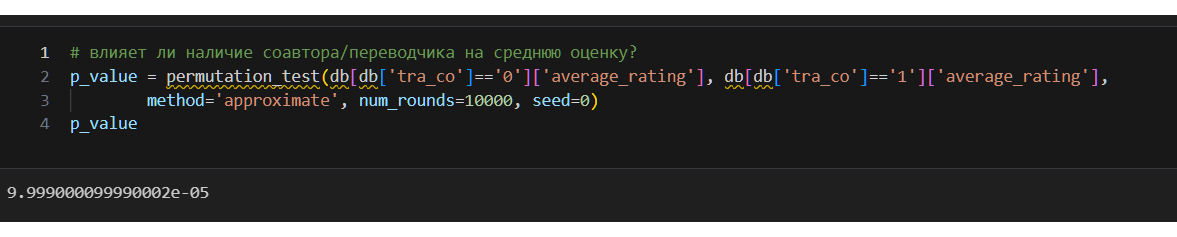
Вижу, что p-value меньше 0.05, поэтому отвергаю нулевую гипотезу о равенстве средних. Принимаю альтернативную гипотезу о том, что средние не равны. Значит для книг с переводчиком, соавтором оценка отличается от книг без переводчиков, соавторов. Это же можно проверить с помощью дисперсионного анализа. У меня выполняются не все условия для классической ANOVA, поэтому применю непараметрический тест Велча.

См. подробнее здесь (https://pingouin-stats.org/generated/pingouin.welch_anova.html?highlight=welch#pingouin.welch_anova).

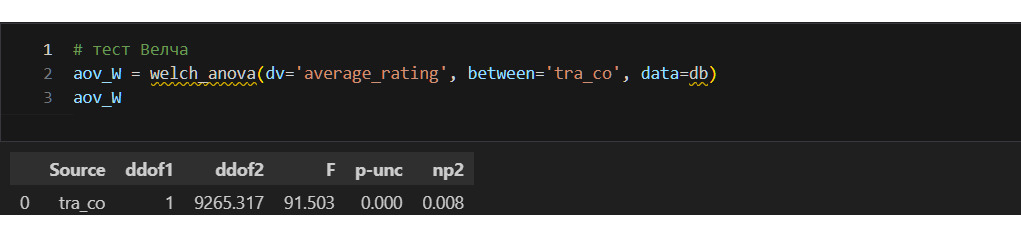
Нулевая гипотеза: средние оценки для книг с соавторами/переводчиками и без них равны. Вижу, что p-value (без корректировки) равно 0.00, значит мы должны отвергнуть нулевую гипотезу и принять альтернативную: средние не равны. Здесь нет смысла искать между какими группами есть отличия, так как таких групп всего две.

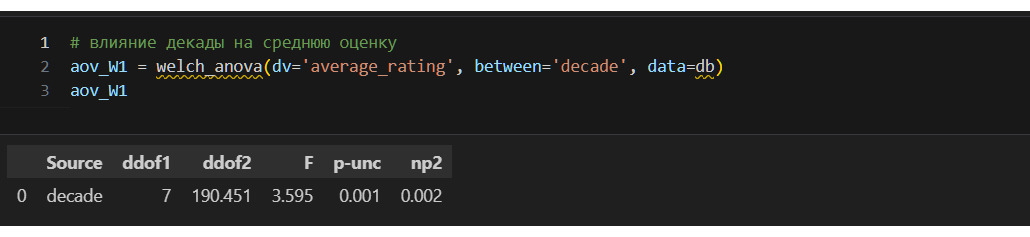
Отвергаю нулевую гипотезу о равенстве средних. Принимаю гипотезу, что средние неравны. Другими словами, средняя оценка зависит от декады, в которой вышла книга.

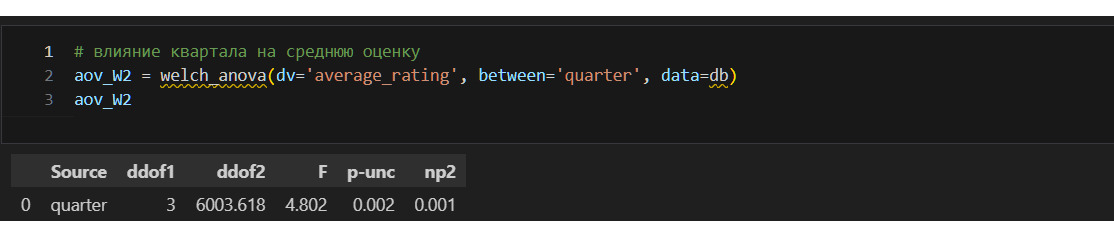
Отвергаю нулевую гипотезу о равенстве средних и принимаю альтернативную гипотезу. Другими словами, средняя оценка зависит от квартала, в котором вышла книга. Здесь дополнительно посмотрю, между какими кварталами есть разница.

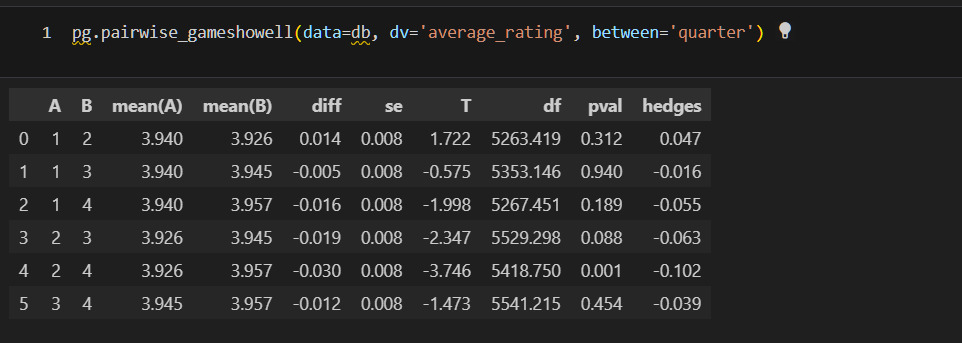
Вижу, что разница есть между вторым и четвертым кварталом (p-value = 0.001).

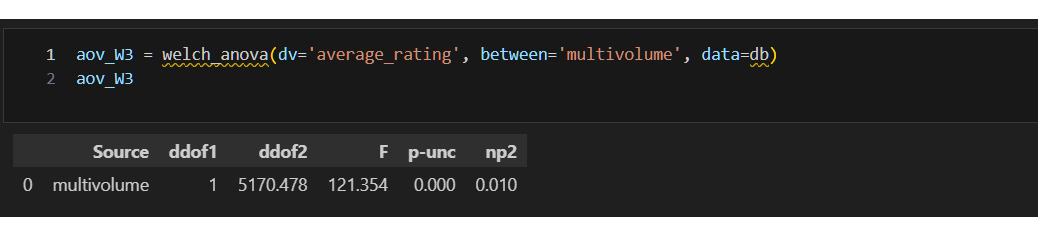
Вижу, что средняя оценка зависит от многотомности издания.

Выводы:

1) На среднюю оценку слабо влияют количественные признаки из данных, в том числе количество страниц в книге.

2) На среднюю оценку влияют категориальные данные, а именно наличие или отсутствие соавтора/переводчика, декада, в которой вышла книга, квартал, в котором вышла книга, а также многотомность издания.

Теперь изучу названия книг, получу для них количественные характеристики и посмотрю, как они влияют на оценку книги. После этого анализ будет завершен.

Анализ названий книг

В этом разделе я проанализирую названия книг. Для этого я применю NLTK и базовые принципы работы с естественным языком.

Прежде всего, некоторые важные заметки по обработке естественного языка из книги Обработка естественного языка (Тушен Ганегедара).

Основные задачи обработки языка:

1) токенизация — разбиение текста на неделимые единицы, например слова;

2) устранение неоднозначности слов. Примеры «Кредитная карта заблокирована» и «Политическая карта Африки»;

3) выделение именованных сущностей, то есть имен, названий организаций, местоположений;

4) морфологическая разметка, то есть определение частей речи, например существительное, глагол;

5) классификация предложений, описаний. Например, калссификация новостных статей по тематикам, классификация отзывов на фильмы на положительные и отрицательные;

6) генерация естественного языка, например для написания новостных статей;

7) создание вопросно-ответственных систем, например чат-ботов;

8) машинный перевод.

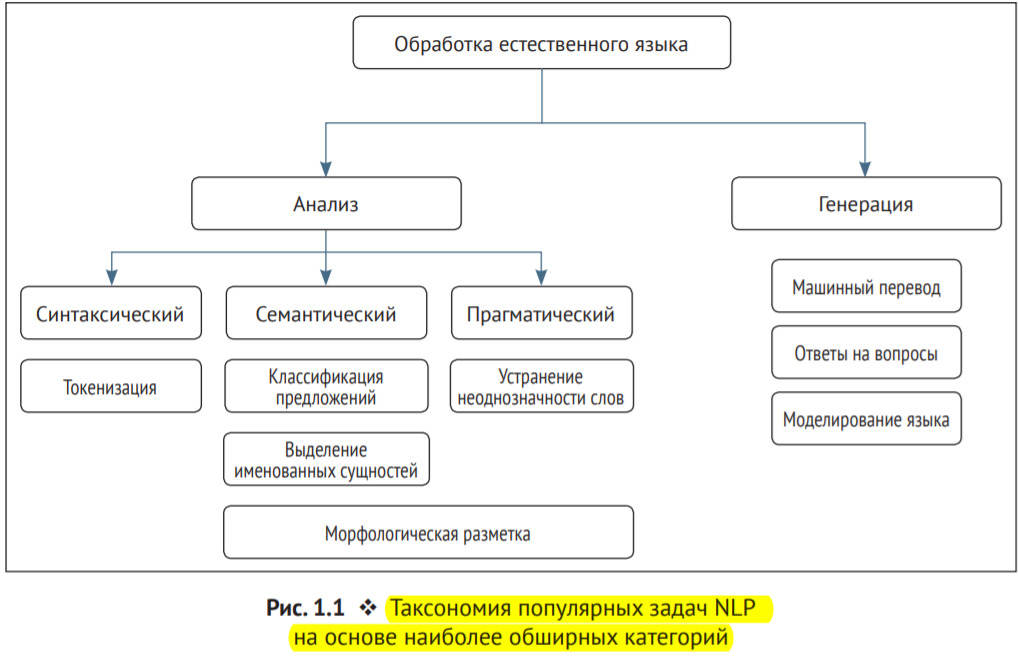
Традиционный подход к обработке языка предполагает:

1) предварительную обработку текста с целью уменьшить словарный запас и удалить помехи,

2) конструирование признаков, например мешок слов.

Начну я вот с чего. В title у нас часто задано не только название книги, но и какая-то характеристика в скобках. Посмотрю на это.

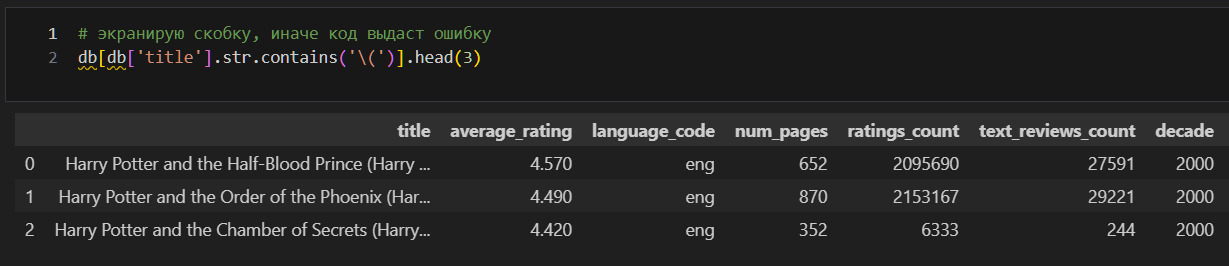
Удалю скобки, но работать буду только с копией таблицы, так как то, что в скобках, само по себе важный признак. Меня же здесь просто интересует название книги.

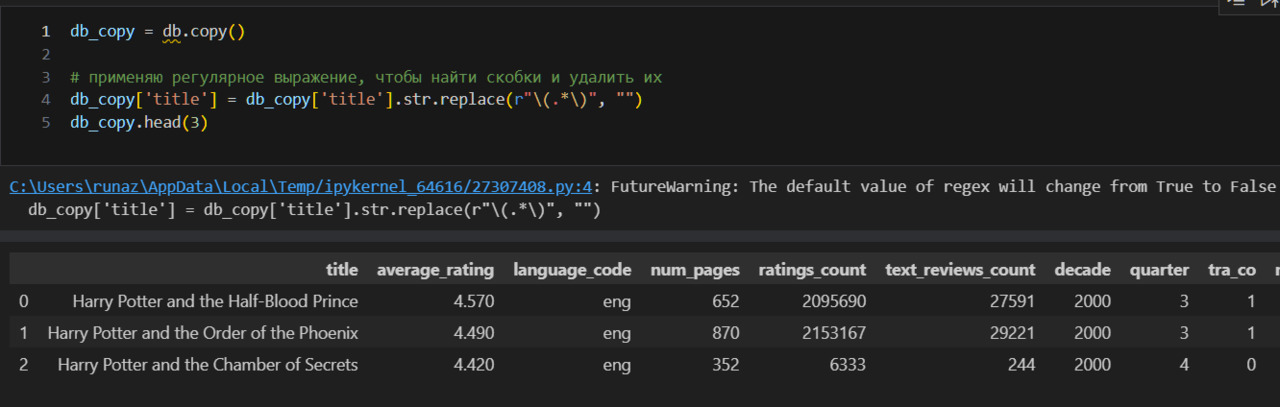
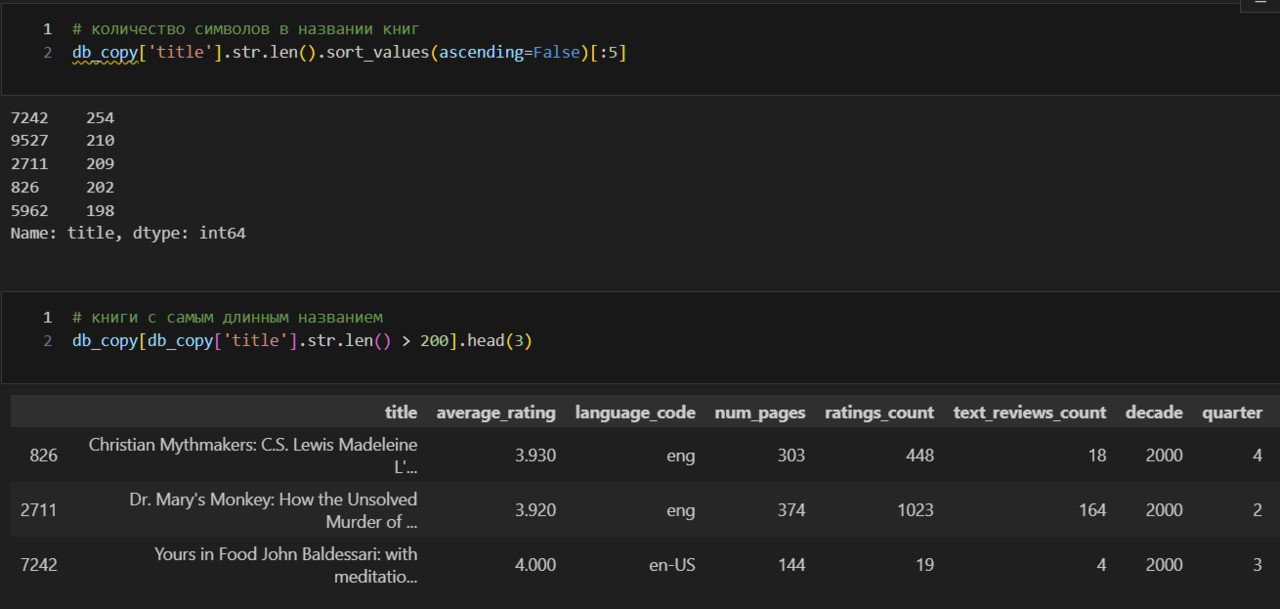
Вижу, что уникальные слова составляют только 19% от всех слов в названиях. Много это или мало? При работе с другими текстами я встречал, например, 5%. И это были вполне классические книги. Так что можно полагать, что названия книг достаточно разнообразны. Но интересно, насколько длинные слова используют в названиях книг.

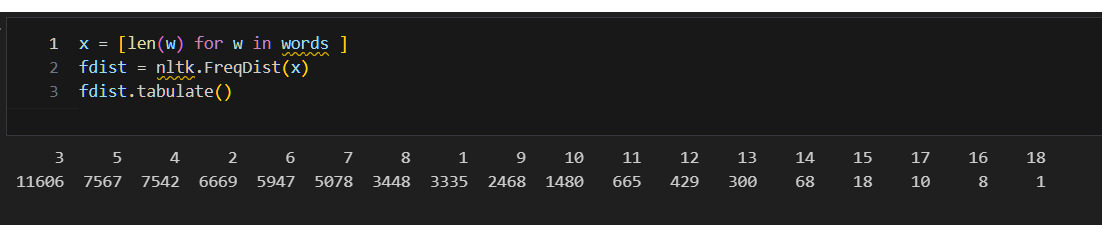
Слова в основном короткие — три знака. Хорошо, теперь еще раз проведу деление на слова (токенизацию), но уже другим способом.

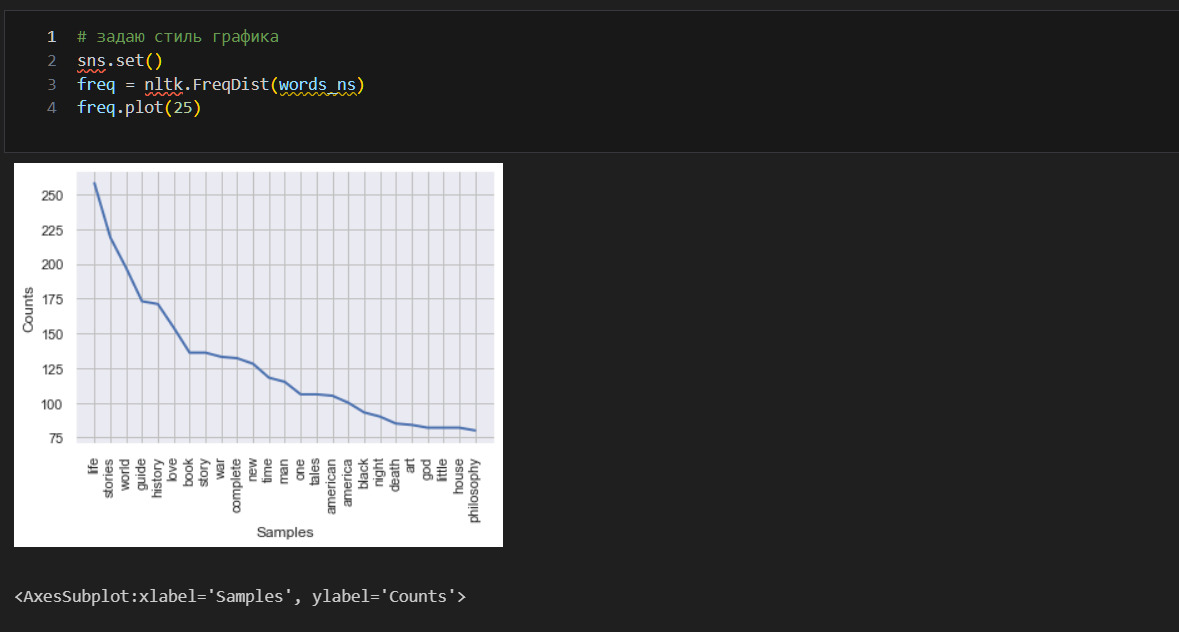
Теперь я хочу произвести те же операции, но на датафрейме, чтобы получить дополнительные признаки. Это также пример на лямбда-функцию, в том числе совместно с генератором.

Две оценки (-0.5, 0.875) означают следующее. Первая оценка — это негативный/позитивный заголовок (от -1 до 1, ближе к 1 позитивный, ближе к -1 негативный, 0 нейтральный). Вторая оценка — это объективный/субъективный заголовок (от 0 до 1, ближе к 1 субъективный).

Я получил три новых признака: длина названия, эмоциональная окраска, субъективность. Теперь применю статистический анализ. У меня только количественные признаки, установить я хочу корреляцию. Распределение **average_rating** не является нормальным. Поэтому применю корреляцию Спирмена.

Корреляция Спирмена

Когда применяется

Если не выполняются условия для корреляции Пирсона.

Альтернативы, если условия не выполняются

1) гамма Гудмана и Краскелла;

2) тау Кендела;

3) d Сомерса.

Интерпретация

Нулевая гипотеза: нет связи между двумя переменными, то есть r = 0 в генеральной совокупности.

Чем ближе к 1, тем сильнее связь.

Особенности

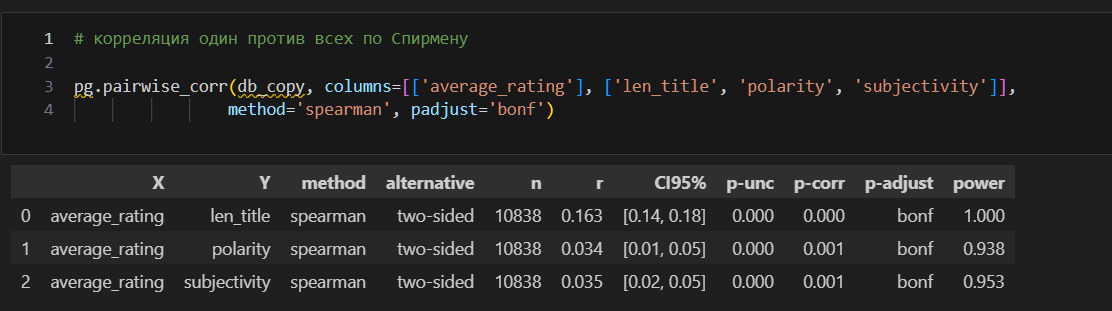
Видно, что нет значимой корреляции ни с одним признаком. Создам облако слов для книг с положительными и отрицательными оценками.

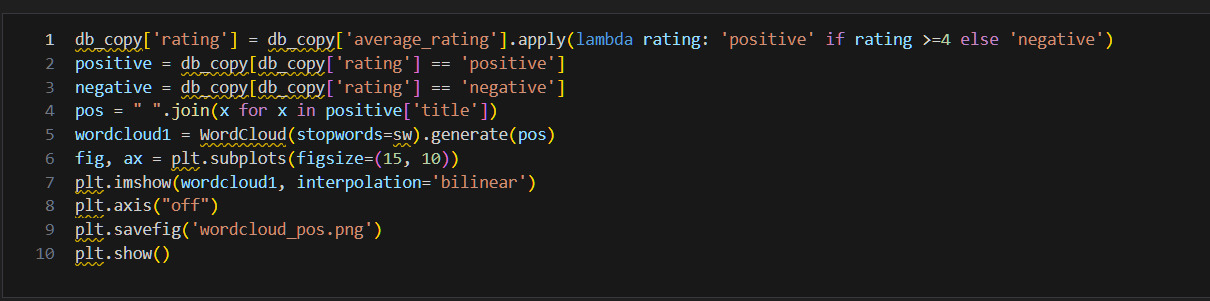
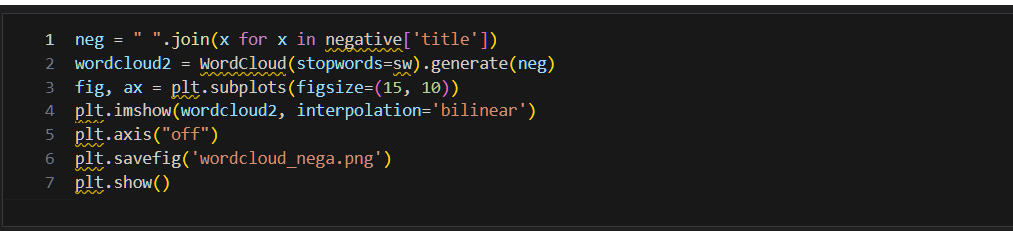
Сохранение данных